 |
Главная |
Производная по направлению. Градиент
|
из
5.00
|
Частные производные  и
и  представляют собой производные от функции z = f(x; y) по двум частным направлениям осей Ox и Oy (рисунок 43).
представляют собой производные от функции z = f(x; y) по двум частным направлениям осей Ox и Oy (рисунок 43).
 |
Рисунок 43
Пусть функция z = f(x; y) определена в некоторой окрестности точки М(х; у),  – некоторое направление, задаваемое единичным вектором
– некоторое направление, задаваемое единичным вектором  где
где 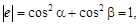 ибо
ибо  (или
(или  ); cos a, cos b – косинусы углов, образуемых вектором е с осями координат и называемые направляющими косинусами.
); cos a, cos b – косинусы углов, образуемых вектором е с осями координат и называемые направляющими косинусами.
При перемещении в данном направлении  точки M(x; y) в точку M1(x + Dx; y + Dy) функция z получит приращение D
точки M(x; y) в точку M1(x + Dx; y + Dy) функция z получит приращение D 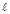 z = f(x + Dx; y +
z = f(x + Dx; y +
+ Dy) – f(x; y), называемое приращением функции 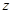 в данном направлении
в данном направлении 
Если  то, очевидно, что
то, очевидно, что 
 следовательно,
следовательно, 
Производной  по направлению
по направлению  функции двух переменных
функции двух переменных
z = f(x; y) называется предел отношения приращения функции в этом направлении к величине перемещения  при стремлении последней к нулю, т. е.
при стремлении последней к нулю, т. е.

Производная  характеризуетскорость изменения функции в направлении
характеризуетскорость изменения функции в направлении 
Формула для производной функции z = f(x; y) по направлению имеет вид
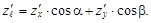
Пример 16.Дана функция z = x2 + y2, в точке M(1; 1) направление составляет с осью Ox угол  Найти производную функции по указанному направлению в этой точке.
Найти производную функции по указанному направлению в этой точке.
Решение
Так как 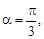 то угол
то угол  По формуле производной функции по направлению получим
По формуле производной функции по направлению получим

В точке M(1; 1) получаем: 
Градиентом grad z функции z = f(x; y) называется вектор с координатами 
Рассмотрим скалярное произведение векторов  и единичного вектора
и единичного вектора 
Получим

Итак, производная по направлению есть скалярное произведение градиента grad z и единичного вектора, задающего направление 
Градиент функции grad z в данной точке характеризует направление максимальной скорости изменения функции в этой точке.
Пример 17.Найти градиент функции 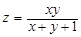 в точке M(0; 1).
в точке M(0; 1).
Решение
По формуле градиента

При х = 0 и у = 1 получаем

Тест 12.Градиент функции  в точке А(1; 1) равен:
в точке А(1; 1) равен:
1) 
2) 
3) 
4) 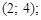
5) 
Дифференцирование сложных и неявных функций
Случай одной независимой переменной
Предположим, что z = f(x; y) – дифференцируемая функция двух переменных x и y в некоторой области D, а аргументы x и y являются дифференцируемыми функциями некоторой переменной t, т. е. x = x(t), 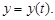 Тогда
Тогда  – функция одной переменной t.
– функция одной переменной t.
Теорема.Имеет место равенство
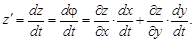
Если  совпадает с одним из аргументов, скажем, t = x, то
совпадает с одним из аргументов, скажем, t = x, то

и  называется полной производной функции z по x.
называется полной производной функции z по x.
Случай нескольких независимых переменных
Если аргументы x и y функции z = f(x; y) являются функциями двух переменных, скажем, x = x(u; v), y = y(u; v), то 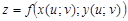 также является функцией двух переменных
также является функцией двух переменных  и v.
и v.
Теорема.Имеют место формулы
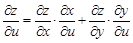 и
и 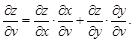
Структура этих формул сохраняется и при большем числе переменных.
|
из
5.00
|
Обсуждение в статье: Производная по направлению. Градиент |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

