 |
Главная |
Задачи на максимум, минимум функции
|
из
5.00
|
На прошлом занятии мы научились находить экстремумы-минимумы и максимумы функции. На этом занятии надо рассмотреть применение производной для нахождения наибольших и наименьших величин.
Во многих математических моделях, описывающих реальные ситуации, исследуется поведение функции на заданном отрезке. В частности нередко возникает задача нахождения наибольшего и наименьшего значений функции.
Пусть дана функция на данном отрезке. Тогда справедливы следующие теоремы:
Теорема 1.Функция достигает на отрезке и своего наибольшего, и своего наименьшего значений.
Теорема 2. Наибольшего и наименьшего значений функция может достигать как на концах отрезка, так и внутри его.
Теорема 3. Если наибольшее (или наименьшее)значение достигается внутри отрезка, то только в стационарной или критической точке.
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти производную функции.
2. Найти критические точки, расположенные внутри отрезка.
3. Вычислить значения функции в критических токах, а также на концах отрезка.
4. Выбрать из этих значений наибольшее и наименьшее.
Пример 1. Найти наибольшее и наименьшее значение функции 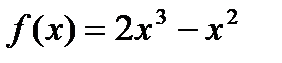 на отрезке хЄ[-1; 1]
на отрезке хЄ[-1; 1]
Решение:
1) 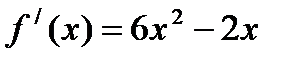
2) 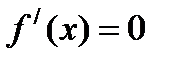
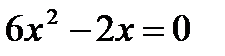
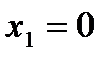
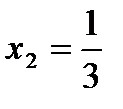
3) Определим принадлежность критических точек данному отрезку
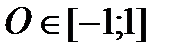
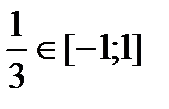
4) Вычислить значение функции в точках
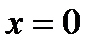 ;
; 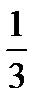 ; -1; 1
; -1; 1
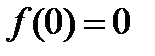
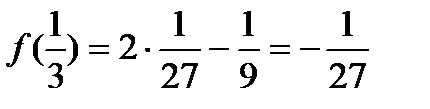
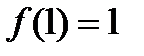
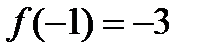
Наименьшее значение 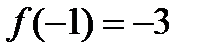
Наибольшее значение 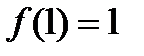
Пример 2. 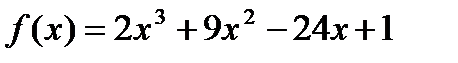 [-2; 1]
[-2; 1]
2) 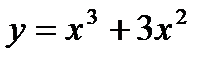 А(-2; 4) В(0; 0) С(-1;2)
А(-2; 4) В(0; 0) С(-1;2)
Решить задачи.
1. Разбить число 20 на 2 слагаемых, произведение которых имело наибольшее значение. (10; 10)
2. Разбить число 10 на слагаемые, чтобы сумма их квадратов была наименьшая. (5; 5)
Домашнее задание
Построить график функции
1) 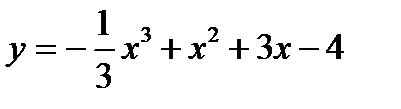
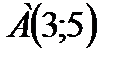
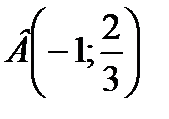
2) 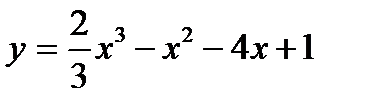
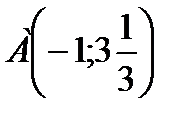
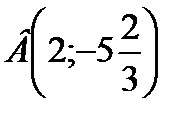
Задача: Разбить тело 30 на 2 слагаемых, чтобы сумма их кубов была наименьшая (15; 15)
Урок № 54. Тема 5. 17. Тема: Дифференциал функции и его геометрический смысл. Применения дифференциала в приближенных вычислениях.
План занятия.
Дифференциал функции и его геометрический смысл.
Применения дифференциала в приближенных вычислениях.
а) понятие бесконечно малой величины.
б) понятие дифференциала функции. Дана функция 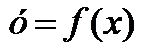
Ее производная 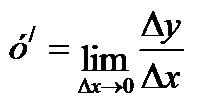 т.е.
т.е. 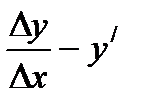 неограниченно
неограниченно
убывает (→0) при ∆х→0 т.е. 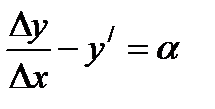 α – б.н.в.
α – б.н.в.
или 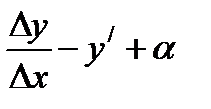 , т.е.
, т.е. 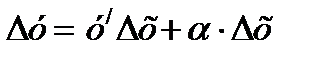
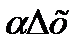 при ∆х→0 стремится к 0 быстрее, чем у/∆х называют главной частью приращения функции
при ∆х→0 стремится к 0 быстрее, чем у/∆х называют главной частью приращения функции 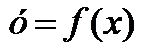 .
.
Определение. Главная часть у/∆х приращение функции 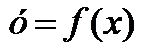 называется дифференциалом функции.
называется дифференциалом функции.
∆х примем 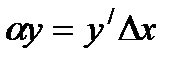
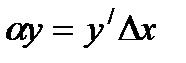
Определение. Дифференциал функции равен произведению функции на дифференциал аргумента.
Решить в аудитории.
Найти ауфункции
1) 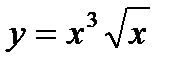 2)
2) 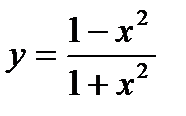 3)
3) 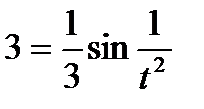
4) 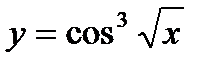 5)
5) 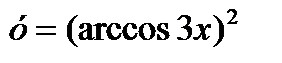
Контрольные вопросы:
1. Что называется дифференциалом функции?
2. Какая величина называется бесконечно малой величиной?
3. Какие свойства приращения функции отражены в понятии дифференциала?
4. Приведите примеры записи связи между физическими величинами в дифференциалах.
5. С помощью какой замены можно получать приближенные формулы?
Домашнее задание.
Найти дифференциалы функций
1) 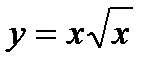
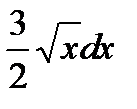
2) 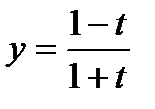
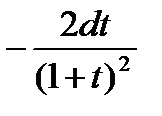
3) 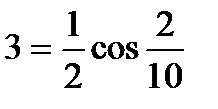
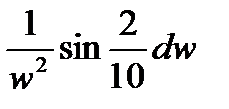
4) 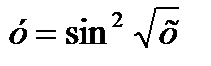
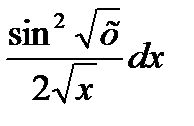
5) 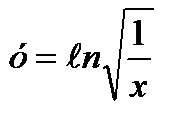
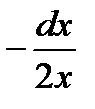
6) 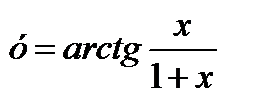
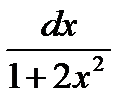
|
из
5.00
|
Обсуждение в статье: Задачи на максимум, минимум функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

