Математическая модель (стандартная) региональной экономики в векторной постановке

Построение модели развития экономики региона представим в виде векторной задачи линейного программирования. Для построения модели используем агрегированную модель экономики региона («отрасли - регион»), являющейся дальнейшим развитием модели («предприятия - отрасли - регион»), представленной в [31, 36, 37].

Введем понятие вектора переменных (управляющих переменных), критериев и ограничений, накладываемых на развитие экономики региона.

Вектор переменных. В его качестве примем:

X(t)={x_j(t), j= 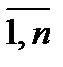} – вектор-столбец, каждая компонента которого определяет валовой объем выпуска продукции j-го вида деятельности в t-ом периоде (tÎТ), показан на рис. 1, где n – множество видов деятельности на уровне разделов и подразделов, в соответствии с ОКВЭД [54], т.е. - это агрегированные виды деятельности, которые примерно соответствуют отраслям в старом понимании этого слова, Т – плановый период.

Y(t)={y_j(t), j= 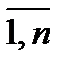} – вектор-столбец, каждая компонента которого определяет конечное использование (конечный спрос) продукции j-го вида деятельности отрасли. Каждая компонента y_j(t) является составной частью вектора x_j(t). Для любой отрасли конечное использование y_j(t) определяется суммой конечного потребления y_j^пот(t), накопления y_j^нак(t) и чистого экспорта y_j^э(t):

y_j(t) = y_j^пот(t)+y_j^нак(t) + y_j^э(t) , j= .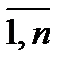

I(t)={I_j(t), j= 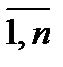} – вектор-столбец, каждая компонента которого определяет валовой объем инвестиций, вкладываемых в увеличение производственных мощностей j-го вида деятельности.

В совокупности они определяют вектор переменных:

X(t) ={X(t), I(t), Y(t)},

размерностью 3*n, который требуется определить на планируемый период tÎТ.

Критерии. Цель развития региона определяется постоянным увеличением благосостояния каждого жителя региона, которое зависит от роста объема выпуска продукции каждого вида экономической деятельности (отрасли) и соответствующей заработной платой с одной стороны, и налоговых отчислений в бюджет государства с другой. Поэтому в качестве критерия примем максимум конечного использования (спроса) каждого вида продукции:

max Y(t) = {max y_j(t), j = }.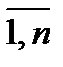

Для оценки региона в целом учитываются агрегированные показатели:

X^val(t)= 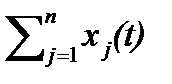- валовой (совокупный) региональный продукт, представляющий сумму валовых выпусков продукции;

Y^val(t)= 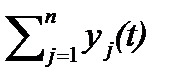- валовое конечное использование, представляющее сумму валового конечного использования выпусков продукции всех видов экономической деятельности.

В совокупности они представляет векторный критерий оптимизации:

Opt F(X,Y)= {max Y(t), max X^val(t), max Y^val(t)}. (6.2.1)

Заметим, что векторная задача позволяет использовать и другие критерии отдельно или, добавляя их к векторному критерию, представленному в (6.2.1).

Ограничения. В модели экономики региона предусматривается три вида ограничений: балансовые, ресурсные и мощности.

· Балансовые ограничения вытекают из анализа межотраслевого баланса.

Валовой объем выпуска производящей отрасли равен сумме стоимостей продукции произведенной этой отраслью и переданной (проданной) во все отрасли и конечной продукцией отрасли:

X_i(t) = 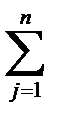a_ijX_j(t) + y_i(t), i= 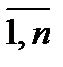, (6.2.2)

где X_i – валовой выпуск продукции i-ой отрасли, 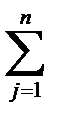a_ijX_j(t) - промежуточное потребление, a_ij – коэффициенты прямых затрат, полученных от i-го вида деятельности, на производство единицы продукции j-го вида деятельности.

Уравнения (6.2.2) называются балансами «выпуска».

Валовой объем выпуска потребляющей отрасли равен сумме материальных затрат на продукцию производимую в других отраслях и денежный доход от производства продукции:

X_j(t) = 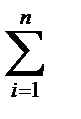a_ij′ X_j(t)+z_j(t), j= , (6.2.3)

где z_j(t) – денежный доход от производства продукции j-ой отрасли, включающей в себя заработанную плату z₁(t), налоги z₂(t), амортизацию z₃(t), прибыль z₄(t) и пр., т. е. z_j(t)=z_1j(t)+z_2j(t)+z_3j(t)+z_4j(t), j= - валовая добавленная стоимость j-го вида деятельности.

Уравнения (6.2.3) называются балансами «затрат».

В матричном виде эти ограничения примут вид:

X(t) = AX(t) + Y(t), X(t)=A′ X(t) + Z(t), (6.2.4)

где A = {a_ij, i,j= } – матрица прямых затрат.

· Ограничения по ресурсам определяются тем, что для производства единицы продукции j-ой отрасли требуются первичные факторы (ресурсы), не являющиеся продукцией других отраслей, к которым относятся труд, земля, полезные ископаемые, финансовые ресурсы и пр.

Обозначим r_ij – объемом затрат i-го ресурса на производство единицы продукции j-ой отрасли:

R = {r_ij, j= 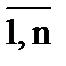, i = }.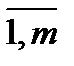

В целом ограничения примут вид:

RX(t) ≤ b(t⁰) + ∆b(t⁰ + ∆t), (6.2.5)

где b(t⁰) = {b_i, i= 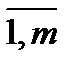} – объемы i-го ресурса, имеющегося в распоряжении региона на начальный период планирования t⁰ÎT;

∆b(t⁰+∆t) = b(t⁰+∆t)-b(t⁰) – вектор приращений учитываемых ресурсов в планируемом периоде (t⁰+∆t), ∆t=0, 1, 2,…,Т.

· Ограничения по мощностям определяются как максимально возможные значения объемов производства X(t) (выраженные в денежных единицах) по всем видам экономической деятельности, которые лежит в пределах:

x_j(t⁰) ≥ x_j(t) ≥ x_j(t⁰+∆t), j= 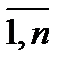, (6.2.6)

где x_j(t⁰) – объемы производства (объемы выполненных работ) j-го вида деятельности в t⁰ (базовом) периоде - практически это отчетные данные за текущий период от (t⁰-1) до t⁰; ∆t – планируемый период времени, как правил один год, (t⁰+∆t)ÎT; x_j(t⁰+∆t) – максимальные объемы производства, которые j-й вид может достичь на планируемый период времени (t⁰+∆t)ÎT.

Региональная экономика направлена на повышения жизненного уровня населения региона, т. е. на увеличение продукции конечного спроса, - это можно выразить критерием (6.2.1) при ограничениях по валовому объему выпуска производящей отрасли – межотраслевой баланс (6.2.2), по ресурсам (6.2.5) и мощностям (6.2.6), в совокупности они представляют векторную задачу линейного программирования:

Opt F(X, I, Y)={Y(t) = {max y_j(t), j = 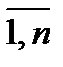}, (6.2.7)

max Y^val(t)= 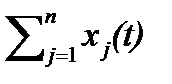, (6.2.8)

max X^val(t)= 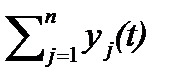}, (6.2.9)

при ограничениях

X_i(t) = 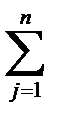a_ijX_j(t) + y_i(t), i= 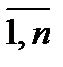, (6.2.10)

RX(t) ≤ b(t⁰+∆t) + ∆b(t), (6.2.11)

x_j(t⁰) ≥ x_j(t) ≥ x_j(t⁰+∆t), j= 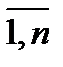, t⁰+∆t= t⁰, t⁰+1, …, t⁰ +T, (6.2.12)

Решение векторной задачи линейного программирования (6.2.7)-(6.2.12) основано на нормализации критериев и принципе гарантированного результата.

Тема 8. Территориальное планирование и региональные рынки -(МАО). (8 час.) [6, с. 73-114]

Общая характеристика рынка региона (2 час.).

Место региональных рынков в воспроизводительном процессе (2 час.).

Математическое моделирование спроса и предложения (2 час.).

Математическое моделирование рыночной структуры (2 час.).

Тема 8. Территориальное планирование и региональные рынки

Рыночная система рассматривается, как процесс целенаправленного взаимодействия товаропроизводителей за наиболее выгодные условия производства и сбыта товаров, а также товаропотребителей, стремящихся получить этот товар по наиболее низкой цене с высоким качеством. Эта целенаправленность находит отражение в моделях спроса и предложения. Математическая модель рынка представлена в виде векторной задачи в двух вариантах: в первом учитываются цели (критерии) каждого потребителя и производителя, а также вектор переменных и ограничения, накладываемые на производственную деятельность; во втором варианте дополнительно учитывается функция предложения и функция спроса.