 |
Главная |
Шкала попарных сравнений Саати
|
из
5.00
|
| Значение wij | Определение | Пояснение | |
| Территории одинаково опасные (безопасные) | Территории обладают примерно одинаковой опасностью | ||
| Промежуточное значение | |||
| Слабое превосходство | Эксперт считает, что опасность первой территории пары несколько выше, чем второй | ||
| Промежуточное значение | |||
| Сильное превосходство | Эксперт считает, что опасность первой территории пары определенно выше, чем второй | ||
| Промежуточное значение | |||
| Явное превосходство | Эксперт считает, что опасность первой территории пары явно выше, чем второй и статистика это подтверждает | ||
| Промежуточное значение | |||
| Абсолютное превосходство | У эксперта нет никаких сомнений относительно того, что опасность первой территории пары значительно выше, чем второй |
2) оценка согласованности мнений экспертов с целью определения возможности использования полученных результатов. Для этого вычисляют коэффициенты вариации
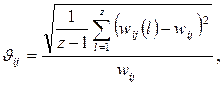
где wij(l) - элементы матрицы W(l), полученной от l-го из z экспертов; 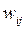 - их усредненные значения. Согласованность считают удовлетворительной при
- их усредненные значения. Согласованность считают удовлетворительной при 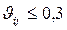 " ij и хорошей при
" ij и хорошей при 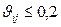 " ij. В случае неудовлетворительной согласованности экспертам предлагается критически оценить результаты сравнений территорий и, при необходимости, внести коррективы. После этого повторяется обработка вновь заполненных матриц попарных сравнений и оценивается согласованность.
" ij. В случае неудовлетворительной согласованности экспертам предлагается критически оценить результаты сравнений территорий и, при необходимости, внести коррективы. После этого повторяется обработка вновь заполненных матриц попарных сравнений и оценивается согласованность.
В результате экспертного оценивания получим z матриц попарных сравнений, которые в общем случае не являются транзитивными.
Обработка матриц попарных сравнений. В качестве весов, полученных в результате экспертного оценивания, принимают компоненты максимального собственного вектора матрицы попарных сравнений W, для вычисления которых используют точный и приближенный способы.
Точный способ. Пусть 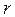 - максимальный собственный вектор матрицы W. С целью вычисления его компонент решим уравнение
- максимальный собственный вектор матрицы W. С целью вычисления его компонент решим уравнение
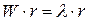 , (14)
, (14)
где 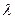 - собственное число матрицы W.
- собственное число матрицы W.
Перепишем (14) в координатной форме:
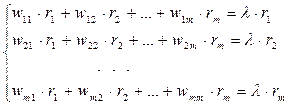 . (15)
. (15)
С учетом того, что при 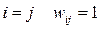 , представим (15) в виде системы однородных уравнений:
, представим (15) в виде системы однородных уравнений:
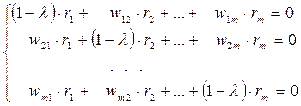 , (16)
, (16)
или, в матричной форме, 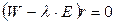 , где
, где 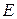 - единичная матрица
- единичная матрица 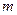 -го порядка. Известно, что система однородных линейных уравнений имеет ненулевое решение только в случае, когда определитель соответствующей матрицы равен нулю:
-го порядка. Известно, что система однородных линейных уравнений имеет ненулевое решение только в случае, когда определитель соответствующей матрицы равен нулю:
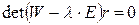 (17)
(17)
Разложив этот определитель, получим характеристическое уравнение 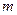 -й степени относительно
-й степени относительно 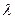 . Решение этого уравнения даст
. Решение этого уравнения даст 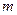 значений
значений 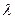 . Затем необходимо найти компоненты собственного вектора матрицы
. Затем необходимо найти компоненты собственного вектора матрицы 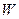 , соответствующего
, соответствующего 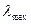 , для чего требуется решение системы однородных уравнений
, для чего требуется решение системы однородных уравнений 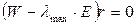 .
.
Пример 1. Пусть имеется матрица
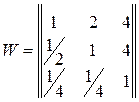
попарных сравнений трех территорий. Определим компоненты максимального собственного вектора матрицы.
Решим уравнение (14) для 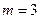 в общем виде, для чего в соответствии с (5.16) представим его в виде системы однородных уравнений
в общем виде, для чего в соответствии с (5.16) представим его в виде системы однородных уравнений
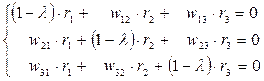 (18)
(18)
Далее из уравнения (17) определим 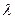 . Раскрывая определитель, получим:
. Раскрывая определитель, получим:
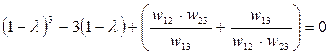 (19)
(19)
Пусть 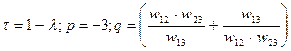 . Тогда уравнение (19) принимает вид неполного кубичного уравнения
. Тогда уравнение (19) принимает вид неполного кубичного уравнения
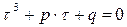 .
.
Его корни определяются по формулам
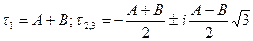 , (20)
, (20)
где 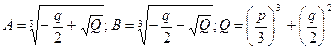 .
.
Анализ (19) показывает, что при невыполнении условия транзитивности матрицы 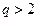 и
и 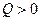 , а при выполнении этого условия
, а при выполнении этого условия 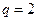 и
и 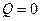 . Это соответствует утверждению о том, что для идеальной матрицы имеет место равенство
. Это соответствует утверждению о том, что для идеальной матрицы имеет место равенство 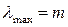 , а для нетранзитивной матрицы
, а для нетранзитивной матрицы 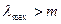 .
.
Уравнение (19) при 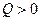 имеет один действительный корень и два сопряженных комплексных корня или при
имеет один действительный корень и два сопряженных комплексных корня или при 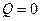 три действительных корня, по крайней мере два из которых будут равны.
три действительных корня, по крайней мере два из которых будут равны.
Подставляя в (18) элементы матрицы 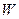 , получим неполное кубичное уравнение
, получим неполное кубичное уравнение 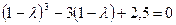 . Обозначив
. Обозначив 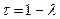 , по (20) найдем:
, по (20) найдем: 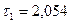 ;
; 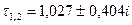 . Следовательно,
. Следовательно, 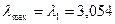 . Подставив значение максимального собственного числа матрицы
. Подставив значение максимального собственного числа матрицы 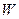 в (19), найдем компоненты максимального собственного вектора, нормированные значения которых и есть значения степеней принадлежности территорий выбранному нечеткому множеству:
в (19), найдем компоненты максимального собственного вектора, нормированные значения которых и есть значения степеней принадлежности территорий выбранному нечеткому множеству: 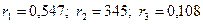 .
.
Необходимо отметить, что при попарных сравнениях четырех и более территорий приведенный способ вычисления максимального собственного вектора матрицы 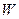 становится сложным для практической реализации.
становится сложным для практической реализации.
Приближенный способ. Введем вектор
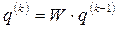 , (21)
, (21)
компоненты которого характеризуют вес территорий, где  - номер шага алгоритма. Тогда нормированный вектор
- номер шага алгоритма. Тогда нормированный вектор 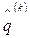 определяется по формуле
определяется по формуле
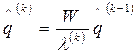 , (22)
, (22)
где 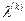 - сумма компонент вектора
- сумма компонент вектора 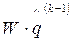 .
.
Если 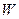 - неразложимая матрица, то процедура (22) сходится, так как при
- неразложимая матрица, то процедура (22) сходится, так как при 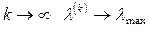 , а
, а 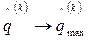 . Вычисление компонент максимального собственного вектора осуществляют до достижения заданной точности
. Вычисление компонент максимального собственного вектора осуществляют до достижения заданной точности 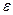 .
.
Пример 2. Решим задачу примера 1 приближенным способом при 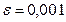 . Результаты представлены в табл. 9.
. Результаты представлены в табл. 9.
Таблица 9
Значения компонент 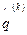 нормированного собственного вектора
нормированного собственного вектора
| qi | k | |||
| q1 | 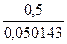
| 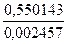
| 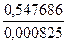
| 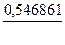
|
| q2 | 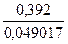
| 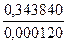
| 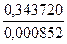
| 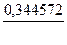
|
| q3 | 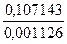
| 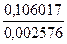
| 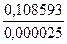
| 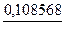
|
Каждая клетка этой таблицы содержит два числа: в числителе - 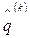 , в знаменателе -
, в знаменателе - 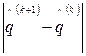 . Требуемая точность вычислений достигается на четвертом шаге итераций. Следовательно, с точностью
. Требуемая точность вычислений достигается на четвертом шаге итераций. Следовательно, с точностью 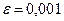 компоненты собственного вектора матрицы
компоненты собственного вектора матрицы 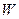 принимают следующие значения:
принимают следующие значения: 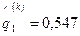 ;
; 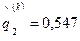 ;
; 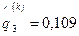 . Приведенный алгоритм приближенных вычислений сравнительно легко реализуем на ЭВМ и позволяет путем увеличения числа итераций достичь любой заданной точности вычислений относительных весов территорий.
. Приведенный алгоритм приближенных вычислений сравнительно легко реализуем на ЭВМ и позволяет путем увеличения числа итераций достичь любой заданной точности вычислений относительных весов территорий.
При удовлетворительной согласованности мнений экспертов определяются степени принадлежности территорий нечеткому множеству 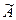 , значения которых равны усредненным (или вычисленным с учетом компетентности экспертов) значениям компонент максимального собственного вектора матриц попарных сравнений, нормированных на единицу: mA(qj)=qj/q1.
, значения которых равны усредненным (или вычисленным с учетом компетентности экспертов) значениям компонент максимального собственного вектора матриц попарных сравнений, нормированных на единицу: mA(qj)=qj/q1.
Методика получения информации об относительной опасности территорий, основанная на рассмотренной нечеткой модели, состоит в следующем:
выбор сравниваемых территорий;
выбор экспертов;
выбор нечеткой переменной, наилучшим образом описывающей опасность территорий;
вычисление степеней принадлежности территорий нечеткому множеству, смысл которого формализован выбранной нечеткой переменной.
Последовательность операций при этом состоит в следующем:
вычисление относительных весов территорий на основе метода попарных сравнений с количественной оценкой предпочтения;
вычисление степеней принадлежности территорий нечеткому множеству.
Вычисление относительных весов территорий производится в следующей последовательности:
выставление оценок парам территорий членами экспертной группы (заполнение матриц попарных сравнений);
обработка матриц попарных сравнений;
объединение относительных весов территорий, полученных экспертами;
оценка согласованности мнений экспертов группы.
|
из
5.00
|
Обсуждение в статье: Шкала попарных сравнений Саати |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

