 |
Главная |
Анализ олигополии с использованием теории игр. Равновесие по Нэшу
|
из
5.00
|
Игра – это любое интерактивное взаимодействие, в котором выбор осуществляется из нескольких вариантов.
Игра с нулевой суммой.
Выигрыш одного равен проигрышу другого.
Игра с ненулевой суммой.
Каждый выигрывает от решения другого.
Терминология теории игр.
Игрок – участник рыночного взаимодействия
Стратегия – любые действия (частные, смешанные)
Платежная матрица – таблица для записи исхода игры каждого игрока
Доминантная стратегия – стратегия, которую всегда выбирает один из игроков
Доминируемая стратегия – стратегия, которую никогда не будет выбрана
Равновесие по Нэшу – набор стратегий, являющийся единственным для каждого игрока и максимизирующей целевую функцию одного игрока при неизменной оптимальной стратегии другого игрока
Рассмотрим платежную матрицу для двух игроков
Каждый игрок может выбрать стратегию А или В
Предположим они принимают решение одновременно (при полной информированности)
| Игрок 1 | |||
| Игрок 2 | А | (0;1) | (2;2) |
| В | (3;0) | (1;3) |
Играем с позиции Игрока 1 (он наблюдает, что предпочтет Игрок 2)
Если Игрок 2 выберет строку А, то для Игрока 1 оптимум В
Если Игрок 2 выберет строку В, то для Игрока 1 оптимум В
Играем с позиции Игрока 2 (он наблюдает, что предпочтет Игрок 1)
Если Игрок 1 выберет строку А, то для Игрока 2 оптимум В
Если Игрок 1 выберет строку В, то для Игрока 2 оптимум А
Таким образом, у игрока 2 нет доминантной стратегии. Но 1-й выберет В, тогда 2-й выберет А=> равновесие по Нэшу (2;2)
Матрица результатов для игр
«Дилемма заключенного»
| Заключенный 1 | |||
| Заключенный 2 | Признаваться | (-1;-1) | (3;-2) |
| Не признаваться | (-2;3) | (2;2) |
Это модель равновесного исхода игры, когда не существует сговора
Предпосылки
Заключенные содержатся в разных камерах
Если оба не признаются, их отпустят (иначе наказание)
Матрица результатов взаимодействия двух фирм
| Стратегия фирмы 2 | Стратегия фирмы 1 | |
| Низкая цена | Высокая цена | |
| Низкая цена | а4;а4 | а3; а2 |
| Высокая цена | а2;а3 | а1; а1 |
Каждая фирма имеет возможность выбрать одну из двух стратегий.
Если обе выбирают высокую, то они получают монопольную цену
Если низкую, то они получают равновесие
Если Фирма 2 выбирает высокую, а первая низкую, то весь рынок или объем спроса переходит Фирме 1
В результате равновесие устанавливается при низких ценах
Примечание: а2>a1>a4>a3
Каждой фирме доступны два вида стратегий:
Стратегия «курка» - назначить высокую цену в момент времени t, если другая фирма установила высокую цену в момент времени (t-1)
Стратегия «хищнечества» назначить низкую цену в любой момент времени
Экономическая концентрация и ее измерение
Рыночная концентрация характеризует число продавцов и характер взаимодействия в рамках одного продуктового рынка.
Индекс Херфиндаля-Хиршмана – сумма квадратов долей всех фирм, действующих на рынке.
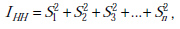
§ IHH- индекс Херфиндаля — Хиршмана;
§ S1 — удельный вес самого крупного предприятия;
§ S2 — удельный вес следующего по величине предприятия;
§ Sn- удельный вес наименьшего предприятия.
IHH max = 1*(100)^2=10 000 или в долях =1 (при монополии)
IHH min=100*(0,01)^2=0,01 (при конкуренции)
Границы индекса: 0,01< IHH ≤1, : 100< IHH < 10 000
Примечание: Чем меньше значение IHH, тем сильнее конкуренция и слабее рыночная власть фирмы. Если все фирмы на рынке характеризуются одинаковым размером одинаковой долей в 1/N, то индекс рассчитывается по формуле.
Коэффициент (индекс) Джини
Определяется как процентная доля размера отрасли, приходящаяся на процентное число фирм, действующих на рынке:
G=P/N
G – коэффициент Джини
N – кумулятивный процент соотв. размера отрасли и рынка
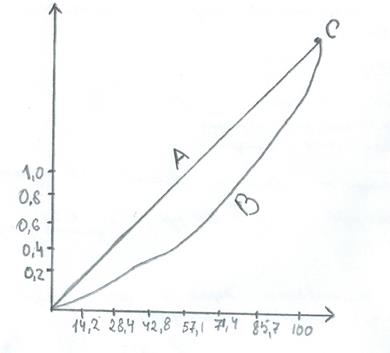
(Точка D=100)
ОС – кривая Лоренца при абсолютном равенстве
ОВС – кривая Лоренца, показывающая какая доля рынка приходится на каждый процент фирмы, действующих на рынке
G=площадь ОАСВ/площадь ОСD
При абсолютном равновесии площадь ОАСВ=0=>G=0
При абсолютном неравенстве площади ОАСВ и OCD равны 1
|
из
5.00
|
Обсуждение в статье: Анализ олигополии с использованием теории игр. Равновесие по Нэшу |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

