 |
Главная |
Примеры выполнения заданий лабораторной работы
|
из
5.00
|
О.Ю. ГОРЛОВА, В.И. Самарин
Лабораторные работы
По математике
Для студентов-бакалавров ОФО
по направлению подготовки «Строительство»
Раздел 1
Сочи ± РИЦ ФГБОУ ВПО «СГУ» ± 2013
УДК 51
ББК 22.1я73
Представлено кафедрой прикладной математики ФИТиМ
Рекомендовано к печати Ученым советом факультета информационных технологий
и математики СГУ (протокол № 3 от 24.11.2012)
Горлова О.Ю., Самарин В.И. Лабораторные работы по математике
Для студентов-бакалавров ОФО по направлению подготовки
«Строительство». Раздел1. – Сочи: РИЦ ФГБОУ ВПО «СГУ», 2013. – 105 с.
Приведены задания лабораторных работ по математике (темы: «Матрицы и определители», «Системы линейных уравнений», «Векторы», «Собственные значения и собственные векторы квадратной матрицы», «Прямая и плоскость», «Кривые второго порядка», «Пределы и непрерывность функций одной переменной», «Дифференциальное исчисление функций одной переменной»). По каждой лабораторной приводится теоретический минимум и примеры выполнения заданий.
УДК 51
ББК 22.1я73
© О.Ю. Горлова, В.И. Самарин, 2013
© ФГБОУ ВПО «СГУ», 2013
| |
Лабораторная работа №1
Матрицы и определители
Теоретический минимум
1. Матрица.
2. Квадратная матрица.
3. Единичная матрица.
4. Произведение матриц.
5. Определитель квадратной матрицы.
6. Минор элемента aijопределителя.
7. Алгебраическое дополнение элемента aijопределителя.
8. Обратная матрица.
Задания
1. Вычислить определители: а) 2-го порядка; б) 3-го порядка тремя способами; в) 4-го порядка:
| № | Определители | № | Определители |
а) 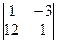 ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б) 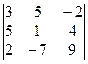 ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в) 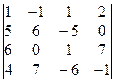 . .
| ||
а) 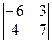 ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б) 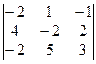 ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б) 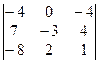 ;
в) ;
в)  . .
| ||
а)  ; б) ; б)  ;
в) ;
в)  . .
| а)  ; б) ; б)  ;
в) ;
в)  . .
|
2. Перемножить матрицы:
| № | А×В | № | А×В |
1 
| 
| Найти  , если А = , если А = 
| |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
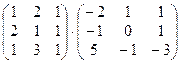
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
3. Найти  :
:
| № | Матрица А | № | Матрица А | № | Матрица А |

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||
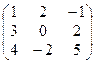
| 
| 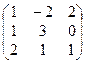
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
|
Справочный материал
к 1-й лабораторной работе
1. Матрица размера m×n – таблица А = (aij)m×n, в которой m строк и n столбцов; aij– элемент матрицы, который находится в i-й строке и в j-м столбце (элементом матрицы может быть число, алгебраическое выражение, функция и т.д.).
2. Транспонированная матрицаАТк матрицеА − матрица, строки которой являются соответствующими по номерам столбцами исходной матрицы А; при транспонировании матрицы А размера m´n получается матрица АТ размера n´m.
3. Квадратная матрица n-го порядка – матрица, у которой n строк и n столбцов; квадратные матрицы соответственно первого, второго и третьего порядка:
А1´1=(a11); A2´2=  ; A3´3=
; A3´3=  .
.
4. Главная диагональ квадратной матрицы – диагональ от левого верхнего угла к правому нижнему углу матрицы, т.е. проходящая по элементам матрицы с одинаковыми индексами: a11, a22, …, ann; вторая диагональ (от левого нижнего угла к правому верхнему углу) называется побочной диагональю квадратной матрицы.
5. Диагональная матрица – квадратная матрица, все элементы которой, не стоящие на главной диагонали, – нули.
6. Единичная матрицаЕ – диагональная матрица, все элементы которой на главной диагонали – единицы; Еn − единичная матрица n-го порядка.
7. Треугольная матрица – квадратная матрица, все элементы которой ниже главной диагонали – нули.
8. Трапецеидальная матрица – матрица, в которой число нулей, стоящих с начала каждой следующей строки, превышает это число нулей в предыдущей строке, все нулевые строки, если они имеются в матрице, расположены ниже последней ненулевой строки, а число столбцов матрицы больше числа ненулевых строк.
9. Матрица ступенчатого вида– треугольная матрица и трапецеидальная матрица.
10. Равенство матриц:две матрицы одинакового размера A = (aij)m´n и B = (bij)m´n равны, если равны все их соответствующие элементы: aij= bij; обозначение равенства матриц: A = B.
11. Произведение матриц при умножении матрицыA = (aij)m´qслева на матрицуB = (bij)q´n– матрица C =(сij)m´n= AB, у которой элемент сij, стоящий в i-й строке и j-м столбце, равен сумме парных произведений элементов i-й строки матрицы А и соответствующих по номерам элементов j-го столбца матрицы B: сij= ai1∙b1j+ ai2∙b2j+ …+ aiq∙bqj; A(BС) = (АВ)С; A(B + С)= АВ + АС; в общем случае АВ ≠ ВА, однако для квадратной матрицы А n-го порядка: АЕn = ЕnА = А.
Внимание!Матрицу А можно умножить слева на матрицу В, если число столбцов матрицы А равно числу строк матрицы В, при этом матрица С = АВ имеет столько строк, сколько строк у матрицы А, и столько столбцов, сколько столбцов у матрицы В.
12. Элементарные преобразования строк и столбцов матрицы:
Ø взаимная перестановка двух строк или столбцов;
Ø умножение строки или столбца на произвольное ненулевое число (деление на число а ≠ 0 можно рассматривать как умножение на число 1 ∕ а);
Ø прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число, или прибавление к элементам одного столбца соответствующих элементов другого столбца, умноженных на одно и то же число (вычитание можно рассматривать как сложение с умноженным на (–1) вторым слагаемым), что кратко формулируется, как: прибавление к одной строке другой строки, умноженной на произвольное число, или прибавление к одному столбцу другого столбца, умноженного на произвольное число.
13. Эквивалентные матрицы – матрицы, которые могут быть получены друг из друга элементарными преобразованиями; обозначение эквивалентных матриц: А ~ В. Элементарными преобразованиями любую ненулевую матрицу можно привести к эквивалентной матрице ступенчатого вида.
14. Определитель (детерминант) квадратной матрицы Аn = (aij)n×n (обозначение определителя: det A или|A|, или Δ) – алгебраическая сумма произведений элементов матрицы, составленных по определенному правилу:
Ø определитель 1-го порядка det(a11) = a11, т.е. равен самому элементу матрицы;
Ø определитель 2-го порядка  = a11∙a22 − a21∙a12, если знак произведения графически заменить отрезком, соединяющим перемножаемые элементы, то схему вычисления определителя 2-го порядка можно представить, как:
= a11∙a22 − a21∙a12, если знак произведения графически заменить отрезком, соединяющим перемножаемые элементы, то схему вычисления определителя 2-го порядка можно представить, как:
 |
Ø  определитель 3-го порядка
определитель 3-го порядка  вычисляется по правилу треугольников, илииначе поправилу Саррюса, т.е. по схеме:
вычисляется по правилу треугольников, илииначе поправилу Саррюса, т.е. по схеме:
(т.е. определитель 3-го порядка равен сумме произведений из трех множителей, равных элементам на главной диагонали и находящихся в вершинах двух треугольников, одна из сторон которых параллельна главной диагонали, минус сумма произведений из трех множителей, равных элементам на побочной диагонали и находящихся в вершинах двух треугольников, одна из сторон которых параллельна побочной диагонали);
Ø определитель любого порядка можно вычислять разложением по какой-либо строке или какому-либо столбцу (это приводит к последовательному уменьшению порядка определителя, а определитель до 3-го порядка уже можно рассчитать указанными способами): определитель равен сумме произведений элементов произвольно выбранной строки (произвольно выбранного столбца) на соответствующие им алгебраические дополнения Аij=(−1)i+j∙Mij, где Mij– минор элемента aij, т.е. определитель, получаемый из элементов матрицы после вычеркивания i-й строки и j-го столбца, на пересечении которых стоит этот элемент.
15. Свойства определителей:
Ø если в матрице имеется нулевая строка или нулевой столбец, то ее определитель равен 0;
Ø если матрица содержит две одинаковые или пропорциональные строки (два одинаковых или пропорциональных столбца), то ее определитель равен 0;
Ø общий множитель элементов строки (столбца) можно выносить в качестве множителя перед определителем;
Ø определитель не изменится, если к строке матрицы прибавить другую строку, умноженную на любое число, что справедливо и для столбцов матрицы;
Ø если две строки (два столбца) поменять местами, то определитель изменит знак на противоположный;
Ø определитель треугольной матрицы равен произведению ее элементов на главной диагонали;
Ø det (A×В) = det (A)×det(В), где A и В – матрицы одного порядка;
Ø det AТ = det A, где АТ– транспонированная матрица к квадратной матрицеА, т.е. матрица, строки которой являются соответствующими по номерам столбцами исходной матрицы А.
16. Обратная матрица к квадратной матрицеА – матрица А−1, для которой выполняется условие АА−1= А−1А = Е, где Е – единичная матрица, порядок которой совпадает с порядком матрицы А. Обратная матрица А−1 существует и определяется однозначно, только если det A ¹ 0.
17. Матричный метод нахождения обратной матрицы:
Ø приставить к матрице А справа единичную матрицу Е того же порядка, что и А: (А|Е);
Ø в матрице А выбрать ненулевой элемент (называемый ведущим для столбца, в котором он находится), и с помощью этого элемента элементарными преобразованиями строк матрицы (А|Е) занулить все остальные элементы этого столбца;
Ø мысленно вычеркнуть отработанный ведущий элемент с его строкой и столбцом и выбрать следующий ведущий элемент; операцию по занулению элементов в матрице А завершить, если в каждой ее строке и в каждом столбце окажется только по одному ненулевому элементу;
Ø перестановкой строк и их делением на значения соответствующих ненулевых элементов в левой части преобразуемой матрицы (А|Е) получить в этой части единичную матрицу, тогда в правой части образуется искомая обратная матрица А−1, т.е. (А|Е) ~ (Е|А–1).
18. Расчет обратной матрицыА–1 по алгебраическим дополнениям элементов исходной матрицы:
Ø найти det A и, если он отличен от нуля, продолжить расчет обратной матрицы, если же det A = 0, то сделать вывод, что обратной матрицы для A не существует;
Ø вычислить все алгебраические дополнения Аijэлементов aijматрицы А;
Ø построить матрицу алгебраических дополнений
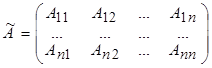 ;
;
Ø построить союзную матрицу А* =  ;
;
Ø записать обратную матрицу А–1 =  ∙А*;
∙А*;
Ø проверить правильность результата, убедившись в выполнении условия А∙А–1 = Е или А–1∙А = Е.
Обратной матрицей для матрицы 2-го порядка А =  является матрица А – 1 =
является матрица А – 1 =  ×
×  .
.
Примеры выполнения заданий лабораторной работы
1o. Вычислить определители: а)  ; б)
; б) 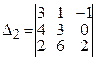 ; в)
; в)  , причем определитель 3-го порядка тремя способами.
, причем определитель 3-го порядка тремя способами.
Решение.
а) Определитель второго порядка  равен произведению элементов на главной диагонали минус произведение элементов на побочной диагонали:
равен произведению элементов на главной диагонали минус произведение элементов на побочной диагонали:
Δ1 = (−4)∙(−2) – [3∙(–5)] =8 – (– 15) = 23.
б)
1-й способ: вычисление определителя по «правилу треугольников».
Согласно «правилу треугольников» получаем:
Δ2=3∙3∙2 + 4∙6∙(−1) + 1∙0∙2 – [2∙3∙(−1) + 6∙0∙3 + 4∙1∙2] =
18 – 24 + 0 – (–6 + 0 + 8) = – 6 – 2 = − 8.
2-й способ: вычисление определителя разложением по строке или столбцу.
Выберем для разложения третий столбец, содержащий 0, тогда получим
Δ2 = (−1)∙А13 + 0∙А23 + 2∙А33 = (−1)∙(−1)1 + 3 ∙  + 2∙(−1)3 + 3 ∙
+ 2∙(−1)3 + 3 ∙  = −18 +10 = − 8.
= −18 +10 = − 8.
3-й способ: вычисление определителя после его предварительного преобразования.
Используем свойство: определитель треугольной матрицы равен произведению ее элементов на главной диагонали.
Для приведения заданного определителя 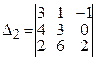 к треугольной форме воспользуемся следующими свойствами определителей:
к треугольной форме воспользуемся следующими свойствами определителей:
· если две строки (два столбца) поменять местами, то определитель изменит знак на противоположный (т.е. чтобы при этом сохранить значение определителя, его следует умножить на – 1);
· если к строке, умноженной на а, прибавить другую строку, умноженную на b, то определитель изменит свое значение в а раз (т.е., чтобы он не изменил своего значения, надо одновременно с указанной операцией сложения строк, разделить определитель на число а);
· общий множитель элементов строки (столбца) можно выносить в качестве множителя перед определителем.
Преобразования определителя выполняем в следующей последовательности:
|
|
 =
=  =
=  =
=
| |||
|
=  =
=  =
=
= (–1)×8× 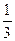 ×(–1)×3×(–1) = – 8.
×(–1)×3×(–1) = – 8.
в) Определитель  можно вычислить разложением по строке или по столбцу. Например, при разложении определителя по 1-й строке получим:
можно вычислить разложением по строке или по столбцу. Например, при разложении определителя по 1-й строке получим:
Δ3 = 4∙А11 + (−1)∙А12 + 1∙А13 + 0∙А14,
где А11, А12, А13, А14 – алгебраические дополнения соответствующих элементов 1-й строки.
Однако можно уменьшить число слагаемых, если, используя свойства определителей и выполнив соответствующие преобразования, увеличить число нулей в 1-й строке:
|
|
 =
=  =
=  =
=
 =
=  = 1×(–1)×(–1) + (–3)×1×5 + 5×(–3)×(–4) – [(–4)×(–1)×5 + (–3)×5×(–1) + 1×(–3)×1] = 1 – 15 + 60 – (20 + 15 – 3) = 46 – 32 = 14.
= 1×(–1)×(–1) + (–3)×1×5 + 5×(–3)×(–4) – [(–4)×(–1)×5 + (–3)×5×(–1) + 1×(–3)×1] = 1 – 15 + 60 – (20 + 15 – 3) = 46 – 32 = 14.
Ответ:Δ1 = 23; Δ2 = – 8; Δ3 = 14.
2o. Перемножить матрицы: а) найти матрицу С = А×В, если матрица  , матрица
, матрица  ; б) найти матрицу С = А2, если
; б) найти матрицу С = А2, если  .
.
Решение.
а) Проверяем существование матрицы С = А×В: матрицу А можно умножить на матрицу В, поскольку число столбцов матрицы А (первого множителя) равно числу строк матрицы В (второго множителя), равно 3. Следовательно, С = А×В существует.
Определяем размер матрицы С = А×В: число строк матрицы С равно числу строк матрицы А (первого множителя), т.е. матрица С имеет 2 строки; число столбцов матрицы С равно числу столбцов матрицы В (второго множителя), т.е. матрица С имеет 3 столбца. Т.о., размер матрицы С: 2´3.
Находим значения элементов матрицы С = А×В. Элемент матрицы С, стоящий в первой строке и в первом столбце, равен сумме попарных произведений элементов первой строки матрицы А и соответствующих элементов первого столбца матрицы В.Элемент матрицы С, стоящий в первой строке и во втором столбце, равен сумме попарных произведений элементов первой строки матрицы А и соответствующих элементов второго столбца матрицы В и т.д.:
 .
.
б) Проверяем существование матрицы С = А2 = А×А: матрицу А можно умножить на матрицу А, поскольку число столбцов матрицы А (первого множителя)равно числу строк матрицы А (второго множителя), равно 3. Следовательно, С = А2, т.е. квадрат квадратной матрицы А, существует.
Определяем размер матрицы С = А2 = А×А: число строк матрицы С равно числу строк матрицы А (первого множителя), т.е. матрица С имеет 3 строки; число столбцов матрицы С равно числу столбцов матрицы А (второго множителя), т.е. матрица С имеет 3 столбца. Т.о., размер матрицы С: 3´3.
Находим значения элементов матрицы С = А2 = А×А. Элемент матрицы С, стоящий в первой строке и в первом столбце, равен сумме попарных произведений элементов первой строки матрицы А и соответствующих элементов первого столбца матрицы А.Элемент матрицы С, стоящий в первой строке и во втором столбце, равен сумме попарных произведений элементов первой строки матрицы А и соответствующих элементов второго столбца матрицы А и т.д.:

 =
=
 =
=  .
.
Ответ: а)  ; б)
; б) 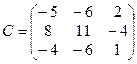 .
.
3o. Найти А–1,если матрица  .
.
Решение.
а) Расчет обратной матрицы матричным методом.
Приставим справа к матрице А единичную матрицу:
(А|Е) =  .
.
В качестве 1-го ведущего элемента используем (– 1) во 3-м столбце матрицы А. С помощью этого элемента зануляем единственный не равный 0 отличный от ведущего элемент этого столбца матрицы А, произведя соответствующее элементарное преобразование строк матрицы (А|Е):
|
(А|Е) =  ~
~  .
.
После мысленного исключения из полученной матрицы строки и столбца использованного ведущего элемента, в оставшихся строках и столбцах матрицы А в качестве следующего ведущего элемента выбираем (– 2) в ее 1-м столбце, и с помощью этого элемента зануляем остальные элементы этого столбца, произведя соответствующие элементарные преобразования строк матрицы (А|Е):
|
 ~
~  .
.
Исключая из рассмотрения строки и столбцы матрицы, образовавшейся на месте матрицы А, в которых находились использованные ведущие элементы, устанавливаем, что для зануления элементов во 2-м столбце в качестве ведущего элемента остался элемент, равный 1:
|
 ~
~  .
.
Т.о., на месте исходной матрицы А получена эквивалентная ей матрица, в каждой строке и в каждом столбце которой имеется только один ненулевой элемент. Чтобы эти элементы приняли значение 1, разделим первую строку полученной матрицы (А|Е) на (– 2) и вторую строку на (– 2):
|
 ~
~  .
.
Чтобы сформировать в левой части полученной матрицы единичную, переставим строки:
|
 ~
~  = (Е|А –1).
= (Е|А –1).
Следовательно, А –1 =  .
.
Проверка: АА −1 =  ∙
∙  =
=
 =
=
=  =
=  = Е, т.е., действительно, обратной к матрице
= Е, т.е., действительно, обратной к матрице  является матрица А –1 =
является матрица А –1 =  .
.
б) Расчет обратной матрицы по алгебраическим дополнениям элементов исходной матрицы.
Имеем: определитель матрицы А равен Δ = det A =  = – 1; алгебраические дополнения элементов аijматрицы системы А:
= – 1; алгебраические дополнения элементов аijматрицы системы А:
А11 = 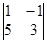 = 8, А12 = –
= 8, А12 = –  = – 5, А13 =
= – 5, А13 =  = 3,
= 3,
А21 = –  = 9, А22 =
= 9, А22 =  = – 6, А23 = –
= – 6, А23 = –  = 4,
= 4,
А31 =  = 3, А32 = –
= 3, А32 = –  = –2, А33 =
= –2, А33 = 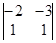 = 1.
= 1.
Составляем союзную матрицу: А* =  =
=  .
.
Следовательно, А−1 =  ×А* =
×А* =  =
=  .
.
Ответ:А –1 =  .
.
|
из
5.00
|
Обсуждение в статье: Примеры выполнения заданий лабораторной работы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

