 |
Главная |
Лабораторная работа № 3. Теоретический минимум
 2016-09-16 |
 1186 |
 Обсуждений (0) |
из
5.00
|
Векторы
Теоретический минимум
1. Коллинеарные векторы.
2. Компланарные векторы.
3. Направляющие косинусы вектора.
4. Проекция вектора на координатную ось.
5. Модуль вектора.
6. Скалярное произведение векторов.
7. Векторное произведение векторов.
8. Смешанное произведение векторов.
9. Приложения скалярного, векторного и смешанного произведений векторов.
10. Условие ортогональности векторов.
11. Условие коллинеарности векторов.
12. Условие компланарности векторов.
Задания
1. Найти координаты, модуль и направляющие косинусы вектора АВ:
| № | Координаты точек А и В | № | Координаты точек А и В |
| A(1; 1; 3), B(2; 2; 3) | A(–2; 1; 3), B(5; 1; 2) | ||
| A(0; 1; 3), B(1; 2; 3) | A(2; –1; 4), B(5; 2; 3) | ||
| A(0; 1; –1), B(1; 2; 0) | A(3; 1; 3), B(2; 2; –1) | ||
| A(2; 2; 3), B(3; 2; 4) | A(2; 2; 3), B(3; 1; 3) | ||
| A(2; 1; 2), B(3; 2; 2) | A(0; 7; 3), B(4; 7; –5) | ||
| A(0; 1; 0), B(1; 2; 2) | A(4; -3; 2), B(1; 2; 3) | ||
| A(0; 1; 4), B(1; 2; 4) | A(5; 1; 1), B(6; 2; 1) | ||
| A(1; 1; 1), B(1; 2; 2) | A(0; 4; 2), B(3; 6; –4) | ||
| A(0; –4; 3), B(1; –3; 4) | A(1; 3; 2), B(4; 6; 5) | ||
| A(1; 2; 1), B(0; 1; 2) | A(0; –2; 1), B(2; 0; 3) | ||
| A(2; 1; 3), B(3; 2; 4) | A(2; –2; 3), B(2; 1; 7) | ||
| A(0; 1; 1), B(1; 2; 2) | A(1; 3; 3), B(2; 4; 2) | ||
| A(2; 1; 3), B(3; 2; 4) | A(2; 0; –1), B(4; 2; 0) | ||
| A(2; 0; 7), B(0; 2; 4) | A(1; 3; –2), B(3; 2; 0) | ||
| A(8; 2; –5), B(7; 1; 4) | A(1; 3; –1), B(3; 1; 0) |
2. Вычислить скалярное и векторное произведения векторов c1= 2a – b и c2= – a + 3b:
| № | Данные | № | Данные |
| a = {–2; 1; 1}, b = {3; –2; 4} | a = {2; 0; 0}, b = {–3; 1; 1} | ||
| a = {0; 1; 1}, b = {–1; –3; 0} | a = {2; 1; 0}, b = {1; 1; 3} | ||
| a = {–2; 1; 1}, b = {0; –2; –5} | a = {1; –1; 0}, b = {0; 3; 2} | ||
| a = {0; 1; 1}, b = {3; –1; 0} | a = {2; 1; –2}, b = {0; 1; 1} | ||
| a = {0; –1; –1}, b = {1; –3; 8} | a = {1; 0; –1}, b = {0; 3; –1} | ||
| a = {0; -1; –1}, b = {2; 0; 2} | a = {2; –1; 4}, b = {–1; 0; 0} | ||
| a = {0; –1; –1}, b = {1; 2; –1} | a = {–1; –1; –1}, b = {0; 3; –1} | ||
| a = {1; –1; 0}, b = {–2; 1; 0} | a = {  ; 1; –2}, b = {1; – ;  }
| ||
| a = {–2; 1; 2}, b = {1; 0; –1} | a = {1; 0; –1}, b = {–1; –3; 0} | ||
| a = {0; 1; 1}, b = {–3; –1; 1} | a = {1; 0; –1}, b = {–1; –3; 0} | ||
| a = {–2; 1; –2}, b = {–1; 0; 3} | a = {5; 2; –2}, b = {3; 3; 4} | ||
| a = {1; –1; –1}, b = {–2; 3; –1} | a = {–1; –1; –1}, b = {0; 0; –1} | ||
a = {–1; 0; –3}, b = {1; 0; –  }
| a = {2; 2; 1}, b = {–2; –3; 0} | ||
| a = {2; –1; 3}, b = {0; 1; 1} | a = {2; –4; 1}, b = {3; 1; –2} | ||
| a = {2; 1; –1}, b = {–1; 0; –2} | a = {0; 2; 1}, b = {2; 1; –3} |
3. Заданы вершины треугольника ABC. Вычислить его площадь и косинус внутреннего угла B.
| № | Вершины треугольника | № | Вершины треугольника |
| A(–1; 3; 3), B(2; 2; 1), C(0; 3; –2) | A(3; –2; 2), B(0; –1; 3), C(5; 2; –2) | ||
| A(2; 3; –1), B(0; 4 ;5), C(–2; –2; 4) | A(3; 4; –2), B(2; 1; 5), C(5; 2; –2) | ||
| A(2; 1; 0), B(3; 0; 3), C(2; –3; 7) | A(5; 0; 4), B(4; –1; 1), C(7; 0; 2) | ||
| A(–3; 1; 3), B(1; 7; 2), C(7; 3; 3) | A(2; –2; 2), B(3; 5; –7), C(4; 8; 0) | ||
| A(0; 2; 1), B(4; 0; 1), C(3; –4; 2) | A(2; 2; 1), B(1; 1; –2), C(4; 0; –1) | ||
| A(0; –2; 1), B(–2; 0; 2), C(0; 1; 0) | A(–1; 2; 7), B(3; 1; 4), C(4; 5; 1) | ||
| A(–1; 2; 1), B(–4;–3; 1), C(5; 4; 2) | A(2; 1; 0), B(1; 1; –3), C(4; 1; –2) | ||
| A(2; 3; –1), B(–3; 4; 1), C(–2; 2; –4) | A(2; 6; –4), B(1; 3; –3), C(4; 4; –4) | ||
| A(3; –4; 6), B(1; –2; 6), C(–3; 5; 1) | A(–1; 2; 0), B(1; 4 ;5), C(–4; 6; 3) | ||
| A(4; –3; 2), B(1; –2; 6), C(6; 3; –2) | A(2; –5; 2), B(1; –3; 2), C(2; –3; 0) | ||
| A(0; –3; 4), B(1; 1; –2), C(5; 0; 4) | A(3; 1; 2), B(2; 3; 2), C(4; –1; 7) | ||
| A(2; –1; 0), B(–2; 1; 1), C(2; 2; –1) | A(–6; 2; 2), B(1; 3; 1), C(0; –4; 2) | ||
| A(–1; 7; 1), B(3; –1; –2), C(–5; 3; 1) | A(2; 1; 7), B(–3; 0; 3), C(2; 4; 2) | ||
| A(1; 1; 0), B(–2; 1; –3), C(–2; –2; 0) | A(1; –1; 4), B(3; 1; 2), C(3; 2; 1) | ||
| A(2; 3; 4), B(–4; 3; 0), C(2; 6; 2) | A(2; 1; 5), B(1; 3; 2), C(4; 5; 3) |
4. Выяснить, компланарны ли векторы a, b, c. Если они не компланарны, то какую тройку (правую или левую) они образуют?
| № | Векторы |
| a = {–2; 1; 1}, b = {0; –2; 4}, c = {2; –1; –1}. | |
| a = {0; 1; 1}, b = {0; 4; –2}, c = {2; 1; 0}. | |
| a = {2; 0; 1}, b = {2; 0; –1}, c = {–2; –1; 4}. | |
| a = {1; –1; –1}, b = {–2; 3; –1}, c = {0; 1; 0}. | |
| a = {1; 1; 1}, b = {2; 3; 0}, c = {3; –1; –1}. | |
| a = {–1; 0; –2}, b = {–3; 2; –1}, c = {2; 0; –2}. | |
| a = {1; 0; 3}, b = {0; 1; 1}, c = {2; –1; 3}. | |
| a = {–3; 1; 4}, b = {2; 0; 0}, c = {–3; 1; 1}. | |
| a = {1; 0; –1}, b = {0; –1; –1}, c = {0; 0; –2}. | |
| a = {–1; 0; –2}, b = {0; 0; –1}, c = {–1; 0; 3}. | |
| a = {–1; 0; –2}, b = {1; 0; –4}, c = {2; 0; –2}. | |
| a = {1; 0; –2}, b = {–3; 2; –1}, c = {4; 2; –3}. | |
| a = {1; 2; 4}, b = {–3; 6; 4}, c = {3; –6; 4}. | |
| a = {1; –1; 1}, b = {1; 1; 1}, c = {2; 3; 4}. | |
| a = {5; 3; –1}, b = {1; –2; 3}, c = {2; 0; –4}. | |
| a = {–3; 3; 3}, b = {2; 1; 1}, c = {19; 11; 17}. | |
| a = {1; 6; 5}, b = {3; –2; 4}, c = {7; –18; 2}. | |
| a = {7; –3; 2}, b = {3; –7; 8}, c = {1; –1; 1}. | |
| a = {2; 1; –1}, b = {1; –4; 1}, c = {3; –2; 2}. | |
| a = {3; 1; –1}, b = {–2; –1; 0}, c = {5; 2; –1}. | |
| a = {3; 3; 1}, b = {1; –2; 1}, c = {1; 1; 1}. | |
| a = {6; 3; 4}, b = {–1; –2; –1}, c = {2; 1; 2}. | |
| a = {1; –2; 6}, b = {1; 0; 1}, c = {2; –6; 17}. | |
| a = {1; –1; –3}, b = {3; 2; 1}, c = {3; 2; 4}. | |
| a = {1; 5; 2}, b = {–1; 1; –1}, c = {1; 1; 1}. | |
| a = {4; 3; 1}, b = {1; –2; 1}, c = {2; 2; 2}. | |
| a = {7; 3; 4}, b = {–1; –2; –1}, c = {4; 2; 4}. | |
| a = {4; 3; 1}, b = {6; 7; 4}, c = {2; 0; –1}. | |
| a = {2; 3; 2}, b = {4; 7; 5}, c = {2; 0; 1}. | |
| a = {–1; 2; 8}, b = {3; 7; –1}, c = {2; 1; 1}. |
5. Решить задачи:
| № | Задачи |
1. Дано: a = {2; 0; – 1} и b = 5i + j – 2k. Найти модуль вектора 2a + b.
2. Определить, перпендикулярен ли вектор c = 3i – j вектору d = 2i + j – k.
3. При каких значениях m и n вектор a = {3; – 7; m} будет коллинеарен вектору b = {6; n; 4}.
4. Найти cos 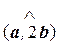 , если a = {2; 0; 0}; b = {1; 1; – 1}.
5. Найти скалярное произведение (a – b)×b, если a = {2; – 1; 1}; b = 3i – 2j – 4k.
6. Найти скалярное произведение (c + 2d)×(2c – d), если |c| = 3; |d| = 4;  = 60°.
| |
1. Дано: c = – i + 2j + 3k, d = 4i – j + k. Найти модуль вектора 3c + d.
2. Определить, перпендикулярны ли друг другу векторы a = 2i – j и b = {– 1; 1; – 2}.
3. При каких значениях α и β вектор m = {5; α; 2} будет коллинеарен вектору n = bi – 6j + 4k?
4. Найти cos  , если a = {2; – 1; 3}; b = 2i + j – k.
5. Найти скалярное произведение (a + b)×(a – b), если a = {3; 0; –2}; b = {2; 4; –1}.
6. Найти скалярное произведение (c + 2d)×d, если |c| = 2; |d| = 3; = 30°.
| |
1. Дано: a = 2i – j + 4k и b = i + 3k. Найти скалярное произведение a×(b – 3a).
2. Дано: |p| = 5; |q| = 2;  = 90°. Найти скалярное произведение (3q – p)×(2q + 4p).
3. При каком значении β вектор m = {9; 3; – 5} будет коллинеарен вектору n = {– 3; – 1; β}?
4. При каком значении α вектор p = {0; 3; – 5} будет перпендикулярен вектору q = {1; 5; α}?
5. Найти cos  , если m = {0; 2; 0}; n = {– 1; 4; 1}.
6. Дано: a = 3i – 2j + 7k. Найти модуль вектора 2a.
| |
1. Даны векторы a = 2i – j + k и b = 3i – j + 2k. Найти модуль вектора a – 2b.
2. Определить, перпендикулярен ли вектор c = {2; – 5; 1} вектору d = {0; 5; – 1}.
3. Дано: |с| = 3; |d| = 6; = 30°. Найти скалярное произведение c×(d – 3c).
4. Дано: a = 2i – j + 3k, b = i + 2j – k. Найти скалярное произведение (a + b)×(2a – b).
5. При каком значении m вектор a = {m; – 3; 4} будет коллинеарен вектору b = {2; – 6; 8}?
6. Найти cos  , если p = {7; 2; – 1}; q = {3; 6; – 3}.
| |
1. Дано: |m| = 4; |n| = 6;  = 60°. Найти скалярное произведение 2m×(m – 2n).
2. Дано: c = {3; 2; – 1}; d = {0; 1; 5}. Найти скалярное произведение 3c×(c + 2d).
3. При каком значении α вектор p = {2; α; 0} перпендикулярен вектору q = {– 1; 3; 1}?
4. Найти модуль вектора a – 2b, если a = 2i – j + k и b = 3i – k.
5. Найти косинус угла между векторами p и q, если p = {1; 2; 3}; q = {6; 4; – 2}.
6. При каком значении α и βвектор m = {5; α; 2} будет коллинеарен вектору b = {β; – 6; 4}?
| |
1. Дано: p = 7i + 2j – k и q = 3i + 6j – 3k. Найти косинус угла между векторами 2p и 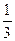 q.
2. Найти модуль вектора c = 2i – 3j – 4k.
3. Дано: a = {5; –1; 2}; b = – i + j. Найти скалярное произведение 2a×(a – 2b).
4. Дано: |p| = 2; |q| = 3; = 90°. Найти скалярное произведение (5p + 3q)×(2p – q).
5. Определить, являются ли векторы c = {– 3; 2; 4} и d = {– 6; 4; 8} сонаправленными.
6. При каком значении α вектор m = {– 8; – α; 0} будет перпендикулярен вектору n = {5; – 2; 1}?
| |
1. Дано: p = i + 2j + 3k, q = 6i + 4j – 2k. Найти косинус угла между векторами 2p и  q.
2. Найти модуль вектора 2p, если p = {– 1; 3; – 7}.
3. Дано: a = {3; – 1; 2}; b = {– 3; 1; – 4}. Найти скалярное произведение (a – b)×(3a + b).
4. Дано: |p| = 8; |q| = 5; = 45°. Найти скалярное произведение (2p + q)×q.
5. Определить, являются ли векторы c = {30; 4; – 2} и d = {– 15; – 2; 1} сонаправленными.
6. При каком значении α вектор a = {2; – 3; 0} перпендикулярен вектору b = ai + j + k?
| |
| 1. Дано: a = {3; – 2; 1}; b = {4; 5; – 2}. Найти косинус угла между векторами 2a и b.
2. Найти модуль вектора – 3с, если с = {2; – 3; 1}.
3. Дано: с = {1; –2; 4}; d = {0; 5; –1}. Найти скалярное произведение d×(2c + d).
4. Дано: |p| = 2; |q| = 4; = 60°. Найти скалярное произведение (p – q)×3q.
5. Определить, являются ли векторы c = {2; – 1; 4} и d = {4; – 2; 8} сонаправленными.
6. При каком значении α вектор m = {2; – 1; 0} будет перпендикулярен вектору n = {α; 8; 1}?
| |
| 1. Даны векторы p = 2i – 3j + 4k, q = – i + j – k. Найти косинус угла между векторами 2p и q.
2. При каких значениях α и βвекторы p = {α; –1; 4}; q = {– 2; – 3; β} коллинеарны?
3. Дано: m = 2i – j + 4k; n = 3i + 2j – k. Найти скалярное произведение 3n×(m – n).
4. Дано: |p| = 4; |q| = 3; = 180°. Найти скалярное произведение (p + q)×2p.
5. Определить, являются ли векторы a = {2; – 1; 4} и b = {6; – 3; 12} сонаправленными.
6. При каком значении b вектор a = {16; b; 0} перпендикулярен вектору b = {– 1; 4; 1}?
| |
1. Даны векторы: m = {2; – 1; 4}; n = –2i + j – k. Найти скалярное произведение (m + n)  (m –2n).
2. Дано: |c| = 3; |d| = 4; = 90°. Найти скалярное произведение (2c + d)×(c –2d).
3. При каком значении  вектор a = {3; – 1; 6} перпендикулярен вектору b = {b; 2; 0}?
4. Найти модуль вектора c – 2d, если c = {2; – 1; 0}; d = {3; – 1; 4}.
5. Даны векторы a = {3; – 2; 0}; b = {1; 3; – 4}. Найти косинус угла между ними.
6. При каких значениях a и b векторы p = {5; a; 2} и q = {b; – 6; 4} коллинеарны?
| |
| 1. Даны векторы: a = {2; – 1; 4}; b = 3i – 3k. Найти скалярное произведение (2a + b) (a – b).
2. Дано: |c| = 3; |d| = 4; = 60°. Найти скалярное произведение d×(c + 2d).
3. При каком значении a вектор a = {– 1; 4; 0} перпендикулярен вектору b = {2; 3a; 1}?
4. Найти модуль вектора 3c + b, если c = {2; – 1; 3}; b = {– 1; 1; – 4}.
5. Даны векторы: a = {3; 2; 1}; b = {– 1; 2; 3}. Найти косинус угла между ними.
6. При каких значениях m и n векторы c = {3; – n; 2} и d = mi + 3j – 2k коллинеарны?
| |
1. Даны векторы: a = {2; – 1; 1}; b = i – 2j + 3k. Найти скалярное произведение (a – b) (2a + b).
2. Дано: |a| = 2; |b| = 3;  = 60°. Найти скалярное произведение 3a×(a +2b).
3. При каком значении a вектор a = {2; – 1; 0} перпендикулярен вектору b = {2a; 1; – 3}?
4. Найти модуль вектора 2a +3b, если a = {2; 0; – 1}; b = {3; 1; – 4}.
5. Даны векторы m = {4; – 1; 2}; n = {3; 1; – 1}. Найти косинус угла между ними.
6. Даны векторы a = {30; 5; – a}; b = 6i + bj – 2k. При каких значениях a и b они коллинеарны?
| |
| 1. Даны векторы: a = – 3i + j – k; b = 5i –4j. Найти скалярное произведение 2a (a – 2b).
2. Дано: |m| = 5; |n| = 4; = 90°. Найти скалярное произведение 2m×(m – 2n).
3. При каком значении a вектор a = {3; – a; 1} перпендикулярен вектору b = {6; 2; 0}?
4. Найти модуль вектора c – 2d, если c = {5; 3; – 2}; d = {1; – 2; 4}.
5.Даны векторы p = {3; 1; 2}; q = {4; – 2; 1}. Найти косинус угла между ними.
6. Даны векторы c = {2; – a; 3}; d = 3i + j + bk. При каких значениях a и b они коллинеарны?
| |
| 1. При каком значении m вектор a = {5; – m; 20} коллинеарен вектору b = {2; 4; 8}?
2. Определить, перпендикулярны ли друг другу векторы c = {2; 1; 1} и d = {– 2; 4; – 3}.
3. При каком значении a равны между собой модули векторов p = {3; a; 0} и q = {0; 5; 0}?
4. Дано: a = 5i – 2j + 4k; b = i – 3j. Найти скалярное произведение a×(b – 3a).
5. Дано: |с| = 3; |b| = 4; = 0°. Найти скалярное произведение с (b – 3с).
6. Даны векторы а = {1; 2; 3}; b= {3; 2; – 1}. Найти косинус угла между ними.
| |
| 1. При каких значениях m вектор c = {2; – 4; 8} коллинеарен вектору d = – i + mj – 4k?
2. Определить, перпендикулярны ли друг другу векторы c = {7; – 4; 4} и d = {0; 2; 1}.
3. При каком значении a равны между собой модули векторов p = {1; – 3; 0} и q = {a; 2; 0}?
4. Дано: m = {3; 2; – 1}; n = – 4i + j – 2k. Найти скалярное произведение n×(2m + n).
5. Дано: |p| = 4; |q| = 8; = 45°. Найти скалярное произведение 3q×(2p + q).
6. Найти косинус угла между векторами 2m и n, если m = {3; – 1; 4}; n = 2i + 5j – 6k.
| |
| 1. При каком значении m вектор a = {2; m; – 4} коллинеарен вектору b = {– 3; 12; 6}?
2. Определить, перпендикулярны ли друг другу векторы c = {– 1; 2; – 3} и d = {2; 3; 1}.
3. При каком значении k равны между собой модули векторов p = 3i – j и q = ki + 8j?
4. Дано: |a| = 2; |b| = 7; = 60°. Найти 3a (a + 2b).
5. Дано: c = 2i – j; d = 4i – 5j + k. Найти скалярное произведение 3с×(с +2d).
6. Найти косинус угла между векторами 2m и n, если m = {2; 1; 0}; n = {0; – 3; 1}.
| |
1. Даны векторы p = {2; – 4; 0} и q = {6; – 2;  }. Найти косинус угла между ними.
2. При каких значениях a и b коллинеарны векторы a = {a; – 1; b} и b = 4i + 3j – k?
3. Найти модуль вектора 3a, если a = 2i – 3j + 4k.
4. При каком значении a вектор p = 2i – 2j перпендикулярен вектору q = 3i – 2j + k?
5. Дано: a = {2; – 1; 3}; b = {4; 0; – 5}. Найти скалярное произведение a×(b –3a).
6. Дано: |p| = 2; |q| = 3; = 45°. Найти скалярное произведение (p + 5q)×(3p – 2q).
| |
| 1. Даны векторы p = 3i – j + 4k и q = 4i + j – 3k. Найти косинус угла между ними.
2. При каких значениях a и b коллинеарны векторы a =2i – aj + 4k и b =6i + 8j + bk?
3. Найти модуль вектора 2a, если a = 3i – 2j + 4k.
4. При каком значении a вектор p = {a; – 1; 0} перпендикулярен вектору q = {2; – 4; – 2}?
5. Дано: a = – 3i + 2j – 4k; b = – i + 3j. Найти скалярное произведение 2a×(a – 2b).
6. Дано: |c| = 2; |d| = 4; = 0°. Найти c (d – 3c).
| |
| 1. Даны векторы p = 2i – 3j + 4k и q = – i + j – k. Найти косинус угла между векторами 2p и q.
2. При каких значениях α и βвекторы p = {α; –1; 4}; q = {–2; –3; β} коллинеарны?
3. Найти модуль вектора c – 2d, если c = {2; –1; 4}; d = {0; 3; – 5}.
4. При каком значении α вектор p = {3; – a; 0} перпендикулярен вектору q = {6; 8; 1}?
5. Дано: a = {2; – 1; 4}; b = {3; – 2; 0}. Найти скалярное произведение (a + 2b)×(a – b).
6. Дано: |c| = 5; |d| = 10; = 60°. Найти скалярное произведение d×(c + d).
| |
1. Дано: a = {2; – 1; 1}; b = {3; 0; 4}. Найти модуль вектора a –2b.
2. Определить, перпендикулярны ли друг другу векторы c = {3; –8; – 4} и d = {0; 2; – 16}.
3. При каких значениях m и n вектор c = {3; – m; 2} будет коллинеарен вектору d =ni + 2j – 4k?
4. Найти cos  , если m = 2i + j + 4k; n = – i + 2j – 3k.
5. Дано: c = i –4j + 3k; d = 5j – 2k. Найти скалярное произведение (2c + d)×d.
6. Найти скалярное произведение q×(2p + q), если |p| = 3; |q| = 8; = 30°.
| |
| 1. Дано: c = 2i – j + 4k и d = 3j – 2k. Найти модуль вектора (c – 2d).
2. Определить, перпендикулярны ли друг другу векторы c = {4; 1; 1} и b = {5; – 3; – 7}.
3. При каких значениях a и b вектор p = {a; – 1; 4}будет коллинеарен вектору q = {2; 3; – β}?
4. Найти 3a (a +2 b), если |a| = 4; |b| = 3; = 60°.
5. Найти скалярное произведение 3a (a + 2b), если a = {4; 0; 3}; b = {– 2; –1; 4}.
6. Дано: |c| = 5; |d| = 6; = 0°. Найти скалярное произведение (3c + d)×d.
| |
| 1. Дано: a = {2; – 1; 4}; b = {3; 2; – 5}. Найти скалярное произведение (3a –2b) (a + b).
2. Дано: |m| = 5; |n| = 4; = 180°. Найти скалярное произведение 2m×(m – 2n).
3. При каком значении b вектор m = {8; b; – 4} коллинеарен вектору n= – 2i –7j + k?
4. При каком значении a вектор p = {a; – 3; 0} коллинеарен вектору q = {2; – 8; 1}?
5. Найти cos , если p = {4; – 2; 1}; q = {3; 1; – 1}.
6. Даны векторы a = 3i – j + k и b = 4j – 3k. Найти модуль вектора a – 2b.
| |
| 1. Дано: c = {3; – 1; 4}; d = {2; 0; – 6}. Найти скалярное произведение d×(2c + d).
2. Дано: |c| = 3; |d| = 4; = 0°. Найти скалярное произведение (3c + d)×d.
3. При каком значении b вектор m = {1; b; – 4} коллинеарен вектору n = {2; 6; – 6}?
4. При каком значении a вектор p = {– 4; 3; 0} коллинеарен вектору q = 5i –aj + 2k?
5. Найти cos , если a = {4; 2; – 1}; b =3i – j + 4k.
6. Дано: a = 2i – j + k; b = 4j + 2k. Найти модуль вектора 3a + b.
| |
| 1. Дано: |p| = 4; |q| = 7; = 45°. Найти скалярное произведение (p + q)×(p – 2q).
2. Дано: m = = 2i – j + 4k; n = 3i – j + 2k. Найти скалярное произведение (m + n)×(2m – n).
3. При каком значении b вектор m = {– 4; b; 8} коллинеарен вектору q = {3; – 2; – 6}?
4. При каком значении a вектор a = {3; – 5; 0} перпендикулярен вектору b = {2; a; 1}?
5. Найти cos , если a = – i + 2j + 4k; b = 3i + 2j – k.
6. Дано: c = 3i –2j + k. Найти модуль вектора 2c.
| |
1. Даны векторы a = {5; 2; – 1} и b = 3i – 4k. Найти модуль вектора 2a + b.
2. Определить, перпендикулярен ли вектор с = –3i – j + 2k вектору d = 3 i – 4j + k.
3. Дано: a = 2i – 3j + k; b = – i + 4j – k. Найти скалярное произведение (a + b)×(2a – b).
4. Дано: |p| = 2; |q| = 7; = 90°. Найти скалярное произведение (p + q)×(2p – q).
5. При каком значении m вектор c = {m; 5; – 4}; коллинеарен вектору d = {– 2; 10; – 8}?
6. Найти cos  , если m = 2i + 6j, n = – i + 8j.
| |
| 1. Даны векторы a = {5; – 1; 4} и b = {0; – 3; – 2}. Найти модуль вектора 2a +3b.
2. Определить, перпендикулярен ли вектор a = {– 1; 4; 3} вектору b = 2i + 3j – 4k.
3. Дано: |m| = 3; |n| = 6; = 0°. Найти скалярное произведение 2m×(m – 2n).
4. Дано: a = 6i – 2j + k; b = – i + 3j – 2k. Найти скалярное произведение (a + b)×(2a – b).
5. При каком значении m вектор c = {3; – m; 6} коллинеарен вектору d = {6; 4; 12}?
6. Найти cos , если m = 3i – j + 3k; n = 2i + j – k.
| |
| 1. Даны векторы: c = 3i – 2j + k; d = i + 3j – k. Найти модуль вектора 3c + d.
2. Определить, перпендикулярен ли вектор c = 2i – j + 3k вектору d = 2i – j – k.
3. Дано: |p| = 4; |q| = 7; = 0°. Найти скалярное произведение (3p + q)×(p – q).
4. Дано: a = 3i – j + 2k; b = – i + j. Найти скалярное произведение 2a×(a –2b).
5. При каком значении b вектор m = {3; – 1} коллинеарен вектору n = {2; b}?
6. Найти cos , если m = 2i + j и n = – i + 3j.
| |
| 1. Дано: a = i – j + 3k; b = 5i – 2j – k. Найти скалярное произведение 2b×(a + b).
2. Дано: |c| = 3; |d| = 2; = 0°. Найти скалярное произведение c×(d – 3c).
3. При каком значении a вектор p = {– 1; a; 0} перпендикулярен вектору q = {2; – 8; 1}?
4. Найти модуль вектора 3a, если a = {2; – 3; 4}.
5. Дано: p = {– 1; 0; – 4}; q = {2; 4; – 6}. Найти косинус угла между векторами p и 2q.
6. При каких значениях a и b вектор c = 3i – aj + 2k коллинеарен вектору d = 4i + j + bk?
| |
| 1. Дано: a = {8; – 1; 0}; b = {4; 5; – 2}. Найти скалярное произведение a×(b – 2a).
2. Дано: |c| = 5; |d| = 3; = 90°. Найти скалярное произведение (c + d)×(c – 2d).
3. При каком значении a вектор p = {3; – 5; 0} перпендикулярен вектору q = {a; 3; 1}?
4. Найти модуль вектора ×p , если p= 6i – 2j – 4k.
5. Дано: a = – i + 2j + 4k; b = – 4j + 3k. Найти косинус угла между векторами a и 3b.
6. При каких значениях a и b вектор d = 2i – aj + 2k коллинеарен вектору a = 2i + 8j – bk?
| |
| 1. Дано: a = – 4i + 3j + 2k; b = – i + 4j + 8k. Найти скалярное произведение 2b×(a – b).
2. Дано: |a| = 7; |b| = 2; = 60°. Найти скалярное произведение 3a×(a + 2b).
3. При каком значении b вектор a = {– 5; b; 0} перпендикулярен вектору b = {4; – 2; 1}?
4. Найти модуль вектора 3p, если p= 2i – j + 2k.
5. Дано: a = 2i – 4j; b = 3i + 7j. Найти косинус угла между векторами a и 2b.
6. При каких значениях m и n вектор c = mi + j – k коллинеарен вектору d = 2i + nj – 4k?
|
Справочный материал
к 3-й лабораторной работе
1. Свободный вектор(далее – вектор)а, или 
, – множество направленных отрезков, имеющих одинаковую длину и одно и то же направление. Параллельный перенос вектора в пространстве (в частности, на плоскости) с произвольным выбором точки для его начала дает тот же вектор; если точка А – начало вектора, точка В – конец вектора, то вектор обозначается как АВ, или 
.
2. Длина (модуль) вектора АВ –длина отрезка АВ; |АВ| − обозначение длины вектора АВ; |а| – обозначение длины (модуля) вектора а.
3. Единичный вектор е – вектор, длина которого равна единице в фиксированном масштабе измерений.
4. Орты i, j, k– единичные векторы вдоль осей прямоугольной системы координат Ох, Оy, Oz соответственно, где О – начало координат, т.е. точка пересечения координатных осей.
5. Направляющие косинусы вектораcos α, cos β, cos γ – косинусы углов, образуемых вектором с координатными осями Оx, Оy и Оzсоответственно.
6. Проекции вектора на координатные осиОx, Оy и Оz:ax = |a|×cos α, ay = |a|×cos β, az = |a|×cos γ, проекции вектора а на координатные оси называются его координатами.
7. Координатное задание вектора а в пространстве: а = {ax; ay; az} = ax×i + ay×j + az×k; координатное задание вектора АВ на плоскости: АВ = {x2 − x1; y2 − y1}, где А(x1; y1) и В(x2; y2) – координаты начала и конца вектора АВ;координатное задание вектораАВ в трехмерном пространстве: АВ = {x2 − x1; y2 − y1; z2 − z1}, где А(x1; y1; z1) и В(x2; y2; z2) – координаты начала и конца вектора АВ.
8. Длина вектора а в прямоугольной системе координат: |a| = 
.
9. Коллинеарные векторы –векторы, расположенные на одной прямой или на параллельных прямых; коллинеарные векторы могут быть одинаково или противоположно направлены; условие коллинеарности векторов а = {ax; ay; az} и b = {bx; by; bz}: ax /bx = ay/by= az /bz; если эти отношения положительны, то векторы а и b сонаправлены, если отрицательны, то противоположно направлены; если хотя бы одна из проекций вектора b равна 0, то условие коллинеарности имеет вид: ax×by= bx×ayи ay×bz = by×az.
10. Компланарные векторы – векторы, расположенные на одной плоскости или на параллельных плоскостях.
11. Два вектора а и b равны,если они одинаково направлены и имеют одинаковую длину; условие равенства векторов а = {ax; ay; az} и b = {bx; by; bz}: а = b, если ax = bx; ay= by; az = bz; в случае а = – b, вектор b называется противоположным вектору а.
12. Координаты алгебраической суммы векторов а = {ax; ay; az} и b = {bx; by; bz}: a± b = {ax ± bx; ay± by; az ± bz}.
13. Координаты вектора а = {ax; ay; az}, умноженного на числоl:lа = {lax; lay; laz}.
14 Скалярное произведение векторов а = {ax; ay; az} и b = {bx; by; bz} – число a∙b, равное произведению длин этих векторов и косинуса угла j между ними: a×b = |a|∙|b|∙cos j = ax∙bx + ay∙by+ az∙bz, в частности, a×а = a2 = ax2 + ay2 + az2 = |a|2. Свойства скалярного произведения векторов:
Ø a×b = b×a;
Ø (λ×a)×b = (λ×b)×a = λ×(a×b);
Ø a×(b + c) = a×b + a×c.
15. Признак перпендикулярности двух ненулевых векторов: если a×b = ax∙bx + ay∙by+ az∙bz = 0, то векторы а = {ax; ay; az} и b = {bx; by; bz} перпендикулярны друг другу.
16. Векторное произведение векторов а = {ax; ay; az} и b = {bx; by; bz} – вектор a ´ b = 
= i∙ 
− j∙ 
+ k∙ 
. Свойства векторного произведения:
Ø вектор a ´ b перпендикулярен векторам а и b;
Ø длина вектора a ´ b равна произведению длин этих векторов и синуса угла j между ними: |a ´ b| = |a|∙|b|∙sin j (0 ≤ j ≤ π);
Ø вектор a ´ b направлен так, что при наблюдении с его конца кратчайший поворот от вектора а к вектору b осуществляется против хода часовой стрелки (т.е. а, b и a ´ b в указанном порядке образуют правую тройку векторов, как и орты i, j, k);
Ø a ´ b = – b ´ a;
Ø a ´ a = 0 ;
Ø (λ∙a) ´ b = a ´ (λ∙b) = λ∙(a ´ b);
Ø (a + b) ´ c = a ´ c + b ´ c;
Ø если a ´ b = 0и a ≠ 0, b ≠ 0, то а и b коллинеарны;
Ø длина вектора a ´ b равна площади параллелограмма, построенного на векторах а и b как на сторонах, при этом вектор a ´ b перпендикулярен плоскости этого параллелограмма;
Ø a ´ (b ´ c) = b × (а×с) – с × (а×b).
Примечание: при нахождении векторного произведения векторов, заданных в координатной плоскости ху, следует их z-координату полагать равной 0.
17. Смешанное произведение векторов а = {ax; ay; az}, b = {bx; by; bz} и с = {cx; cy; cz} – число abc =(a ´ b)∙с = a∙(b ´ с) =
2016-09-16 1186 Обсуждений (0)
