 |
Главная |
Лабораторная работа № 2. Системы линейных алгебраических уравнений
|
из
5.00
|
Системы линейных алгебраических уравнений
Теоретический минимум
1. Однородная и неоднородная система линейных уравнений.
2. Совместная и несовместная система линейных уравнений.
3. Определенная и неопределенная система линейных уравнений.
4. Основная и расширенная матрицы системы линейных уравнений.
5. Ранги основной и расширенной матриц системы линейных уравнений.
6. Теорема Кронекера-Капелли.
7. Формулы Крамера решения систем линейных уравнений.
8. Решение систем линейных уравнений матричным способом.
9. Метод Гаусса решения линейной системы уравнений.
Задания
1. Найти решение систем (1) и (2), используя формулы Крамера, матричным способом и методом Гаусса.
2. Используя метод Гаусса, найти общее и базисное решения системы (3).
| № | Системы | № | Системы | № | Системы |
1. 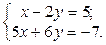 2.
2. 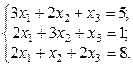 3.
3. 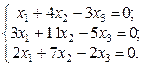
| 1. 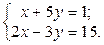 2.
2.  3.
3. 
| 1.  2.
2. 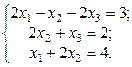 3.
3. 
| |||
1. 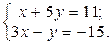 2.
2. 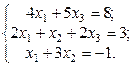 3.
3. 
| 1. 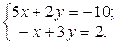 2.
2. 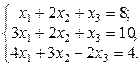 3.
3. 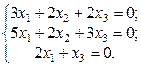
| 1. 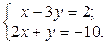 2.
2. 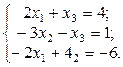 3.
3. 
| |||
1. 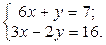 2.
2.  3.
3. 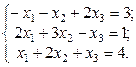
| 1.  2.
2.  3.
3. 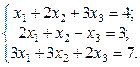
| 1.  2.
2. 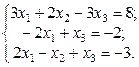 3.
3. 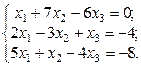
| |||
1. 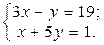 2.
2. 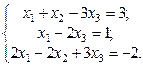 3.
3. 
| 1.  2.
2. 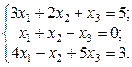 3.
3. 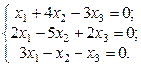
| 1. 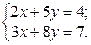 2.
2.  3.
3. 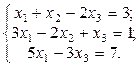
| |||
1.  2.
2. 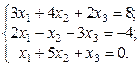 3.
3. 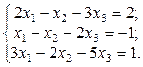
| 1. 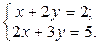 2.
2.  3.
3. 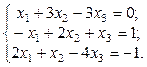
| 1.  2.
2. 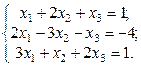 3.
3. 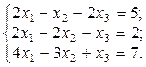
| |||
1. 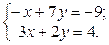 2.
2. 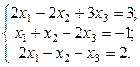 3.
3. 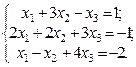
| 1.  2.
2.  3.
3. 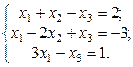
| 1. 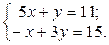 2.
2. 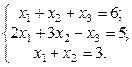 3.
3. 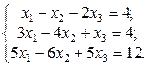
| |||
1.  2.
2.  3.
3. 
| 1. 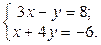 2.
2. 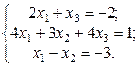 3.
3. 
| 1. 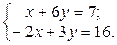 2.
2. 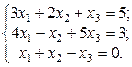 3.
3. 
| |||
1.  2.
2. 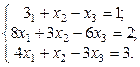 3.
3. 
| 1. 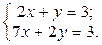 2.
2. 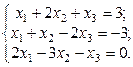 3.
3. 
| 1. 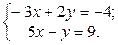 2.
2.  3.
3. 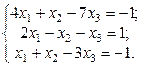
| |||
1. 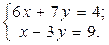 2.
2. 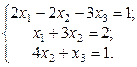 3.
3. 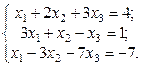
| 1. 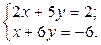 2.
2. 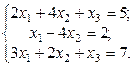 3.
3. 
| 1. 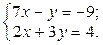 2.
2. 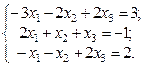 3.
3. 
| |||
1. 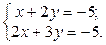 2.
2. 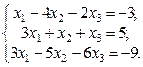 3.
3. 
| 1. 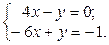 2.
2.  3.
3. 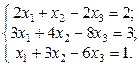
| 1.  2.
2.  3.
3. 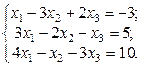
|
Справочный материал
ко 2-й лабораторной работе
1. Системаmлинейных алгебраических уравнений сnнеизвестными–
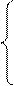 a11∙x1 + a12∙x2 + … + a1n∙xn = b1,
a11∙x1 + a12∙x2 + … + a1n∙xn = b1,
a21∙x1 + a22∙x2 + … + a2n∙xn = b2,
………………………………………
am1∙x1 + am2∙x2 +…+ amn∙xn = bm,
где x1, x2, …, xn – неизвестные, aij (i = 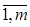 , j =
, j = 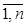 ) – числовые коэффициенты при неизвестных, числа в правой части системы bi (i =
) – числовые коэффициенты при неизвестных, числа в правой части системы bi (i = 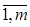 ) – свободные члены системы; отсутствие каких-либо неизвестных в уравнении равносильно наличию нулевых коэффициентов при этих неизвестных.
) – свободные члены системы; отсутствие каких-либо неизвестных в уравнении равносильно наличию нулевых коэффициентов при этих неизвестных.
2. Основная матрица системы линейных уравнений– матрица коэффициентов при неизвестных в системеуравнений:
А =  ,
,
строки матрицы соответствуют уравнениям системы, столбцы – неизвестным.
3. Расширенная матрица системы линейных уравнений– матрица вида
(А|B) = 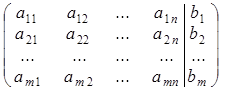 .
.
4. Ранг основной матрицы системы– число ненулевых строк в матрице ступенчатого вида, эквивалентной основной матрицы системы А.
5. Ранг расширенной матрицы системы– число ненулевых строк в матрице ступенчатого вида, эквивалентной расширенной матрицы системы (А|B).
6. Матричная форма записи системы линейных уравнений:A∙X = B, где матрица 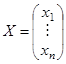 – вектор-столбец неизвестных, матрица
– вектор-столбец неизвестных, матрица 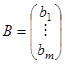 – вектор-столбец свободных членов, А – основная матрица системы.
– вектор-столбец свободных членов, А – основная матрица системы.
7. Однородная система – система уравнений, все свободные члены которой равны нулю; в матричной форме – система с нулевым вектором-столбцом В.
8. Неоднородная система – система уравнений, хотя бы один свободный член которой отличен от нуля.
9. Решение системы – совокупность значений неизвестных, при которых каждое уравнение системы обращается в тождество.
10. Совместная система – системауравнений, имеющая хотя бы одно решение; однородная система уравнений всегда совместна, так как ей удовлетворяет нулевое (тривиальное)решение: x1 = x2 = … = xn = 0.
11. Несовместная система– системауравнений, которая не имеет ни одного решения.
12. Определенная система– совместная системауравнений, имеющая единственное решение.
13. Неопределенная система – совместная системауравнений, которая имеет более одного решения.
14. Теорема Кронекера-Капелли: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы системы.
15. Свободные неизвестные – неизвестные в решении неопределенной системы уравнений, через которые можно выразить все остальные; число свободных неизвестных равно числу неизвестных в системе минус ранг основной (или равный ему ранг расширенной) матрицы системы.
16. Базисные неизвестные – неизвестные, которые в решении неопределенной системы уравнений выражены через свободные; число базисных неизвестных равно рангу основной (или равному ему рангу расширенной) матрицы системы.
17. Частное решение системы – каждое решение неопределенной системы уравнений при заданных значениях свободных неизвестных-параметров.
18. Общее решение системы – совокупность всех частных решений системы уравнений.
19. Базисное решение системы – частное решение неопределенной системы уравнений, в котором все свободные неизвестные приравнены нулю.
20. Формулы Крамера – формулы расчета решения системы n линейных уравнений с n неизвестными A∙X = B, для которой определитель системы Δ= det A ≠ 0: хj = Δj ∕ Δ, где Δj – дополнительные определители системы, j = 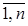 , получаемые из определителя системы заменой соответствующего j-го столбца (т.е. столбца коэффициентов при неизвестной xj) столбцом свободных членов данной системы.
, получаемые из определителя системы заменой соответствующего j-го столбца (т.е. столбца коэффициентов при неизвестной xj) столбцом свободных членов данной системы.
21. Матричный способ решения системы линейных уравнений, для которой Δ = det A ≠ 0: X = А−1∙B, где А−1 – обратная матрица к основной квадратной матрице системы А; матрица В – вектор-столбец свободных членов системы; матрица Х – вектор-столбец неизвестных системы.
22. Метод Гаусса решения системы линейных уравнений – метод решения системы линейных уравнений, предусматривающий прямой ход, в процессе которого расширенная матрица системы (А|B) элементарными преобразованиями ее строк приводится к ступенчатому виду, и обратный ход, в процессе которого последовательной подстановкой найденных значений базисных неизвестных находится решение системы.
|
из
5.00
|
Обсуждение в статье: Лабораторная работа № 2. Системы линейных алгебраических уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

