Лабораторная работа № 6. Кривые второго порядка

2016-09-16

928

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒

Кривые второго порядка

Теоретический минимум

1. Каноническое уравнение окружности.

2. Каноническое уравнение эллипса.

3. Каноническое уравнение гиперболы.

4. Каноническое уравнение параболы.

5. Асимптоты гиперболы.

6. Фокусы эллипса, гиперболы и параболы.

7. Эксцентриситет кривых 2-го порядка.

8. Директрисы кривых 2-го порядка.

9. Определение типа кривой 2-го порядка по ее общему уравнению.

10. Приведение кривой 2-го порядка к главным осям.

Задания

1. Построить кривые по заданным уравнениям. Указать тип кривой.

№	Уравнения кривых 2-го порядка	№	Уравнения кривых 2-го порядка
	а) (х – 2)² + (у – 3)² = 9; б) в) г) у² = 9х.		а) (х – 3)² + (у – 2)² = 9; б) в) г) у² = – 4х.
	а) (х + 3)² + (у – 5)² = 4; б) в) г) у² = 7х.		а) (х – 5)² + (у + 3)² = 4; б) в) г) у² = – 2х.
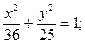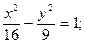	а) (х + 1)² + (у – 2)² = 16; б) в) г) у² = 5х.		а) (х + 1)² + (у + 1)² = 16; б) в) г) у² = – 6х.
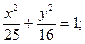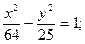	а) (х – 3)² + (у + 4)² = 25; б) в) г) у² = 16х.		а) (х + 4)² + (у – 3)² = 25; б) в) г) у² = – х.
	а) (х + 3)² + (у + 3)² = 4; б) 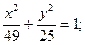в) г) у² = 3х.		а) (х – 3)² + (у – 3)² = 4; б) в) г) у² = – 8х.
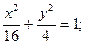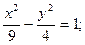	а) (х – 1)² + (у + 1)² = 1; б) в) г) у² = 4х.		а) (х + 1)² + (у – 1)² = 16; б) в) 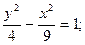г) х² = 9у.
	а) (х + 2)² + (у – 1)² = 9; б) 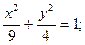в) г) у² = 2х.		а) (х – 1)² + (у + 2)² = 36; б) 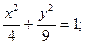в) г) х² = 7у.
	а) (х – 4)² + (у + 2)² = 49; б) 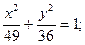в) г) у² = 6х.		а) (х + 2)² + (у – 4)² = 49; б) в) г) х² = 5у.
	а) (х + 4)² + (у – 4)² = 9; б) в) г) у² = х.		а) (х – 4)² + (у + 4)² = 9; б) в) г) х² = 16у.
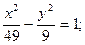	а) (х – 5)² + (у + 1)² = 4; б) в) г) у² = 8х.		а) (х + 1)² + (у – 5)² = 4; б) 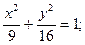в) г) х² = 3у.
	а) (х + 5)² + (у – 6)² = 16; б) в) г) у² = – 9х.		а) (х – 6)² + (у + 5)² = 16; б) 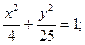в) 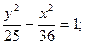г) х² = 4у.
	а) (х – 1)² + (у + 5)² = 1; б) 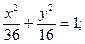в) г) у² = – 7х.		а) (х + 5)² + (у – 1)² = 1; б) 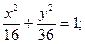в) г) х² = 2у.
	а) (х + 1)² + (у – 3)² = 25; б) в) 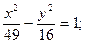г) у² = – 5х.		а) (х – 3)² + (у + 1)² = 25; б) 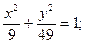в) 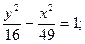г) х² = 6у.
	а) (х – 3)² + (у – 2)² = 36; б) в) г) у² = – 16х.		а) (х – 2)² + (у – 3)² = 36; б) в) г) х² = у.
	а) (х + 2)² + (у + 4)² = 49; б) в) г) у² = – 3х.		а) (х + 4)² + (у + 2)² = 49; б) в) г) х² = 8у.

2. Определить тип кривой второго порядка по ее общему уравнению, привести это уравнение к главным осям и построить соответствующую кривую. Определить координаты вершин и фокусов кривой, записать уравнения директрис и асимптот, если они есть. Вычислить эксцентриситет кривой.

№	Уравнение	№	Уравнение
1	4х² + у² – 8х + 4у = 0		4х² – у² + 16х – 2у + 15 = 0
	9х² – 4у² + 54х + 8у + 41 = 0		х² + 25у² + 4х – 150у + 204 = 0
	2х² + 3у² + 12х – 6у + 15 = 0		4х² – 9у² + 16х + 54у – 101 = 0
	4х² – у² + 8х – 2у + 3 = 0		3х² + 2у² + 12х – 16у + 38 = 0
	9х² + 16у² + 36х – 64у – 44 = 0		9х² – 16у² – 36х – 64у – 172 = 0
	4х² – 25у² + 8х – 10у + 4 = 0		4х² + 9у² + 32х – 16у + 37 = 0
	9х² + 4у² + 36х – 8у + 36 = 0		9х² – 4у² – 18х – 16у – 43 = 0
	х² – 4у² + 10х + 24у – 7 = 0		4х² + у² – 8х + 4у + 24 = 0
	9х² + 4у² + 36х – 8у + 36 = 0		4х² – у² – 16х – 6у + 11 = 0
	х² – 4у² + 6х + 8у + 5 = 0		х² + 4у² + 10х – 24у + 57 = 0
	2х² + 3у² + 8х – 6у + 5 = 0		х² – 4у² + 6х + 8у + 21 = 0
	9х² – 4у² + 36х + 8у + 68 = 0		4х² + 9у² + 32х – 18у + 109 = 0
	4х² + 9у² – 32х + 36у + 64 = 0		5х² + 3у² – 10х + 12у + 17 = 0
	4х² – у² – 8х – 4у – 16 = 0		9х² – 16у² – 54х – 64у – 127 = 0
	9х² + 4у² + 18х – 8у – 23 = 0		4х² + 9у² – 40х + 36у + 100 = 0

3. Решить задачи:

№	Задачи
	Составить уравнение радиуса окружности х² + у² + 4х + 2у – 32 = 0, проведенного в точку А(4; − 2) на ней.
	Составить уравнение эллипса с центром в начале координат и фокусами на оси Оx, если расстояние между его фокусами 16, а эксцентриситет равен 1/2.
	Найти эксцентриситет гиперболы .
	Составить уравнение оси параболы у² – 6у – 12х – 15 = 0.
	Составить уравнение директрисы параболы х² – 4х – 16у + 52 = 0.
	Составить уравнение касательной к окружности х² + у² – 4х – 6у + 8 = 0, проведенной в точке А(3; 5) на ней.
	Найти эксцентриситет эллипса .
	Составить уравнение гиперболы с фокусами на оси Ox, если расстояние между ее фокусами равно 20, а уравнение ее асимптот y = ± .
	Составить уравнение окружности, проходящей через точки А(3; 7) и В(5; − 1) и имеющей центр на оси Оу.
	Найти уравнение кривой на плоскости, отношение расстояний каждой точки которой от точки А(3; 0) и от прямой x = 12 равно λ = 1/2.
	Составить уравнение радиуса окружности х² + у² + 4х + 2у – 21 = 0, проведенного в точку А(3; − 2) на ней.
	Составить уравнение эллипса с центром в начале координат и фокусами на оси Оx, если расстояние между его фокусами равно 12, а эксцентриситет равен 0,3.
	Найти эксцентриситет гиперболы .
	Составить уравнение гиперболы, если уравнение ее асимптот y = ± ×х и она проходит через точку (9; 3 ).
	Составить уравнение параболы, фокус которой лежит в начале координат, а директриса задана уравнением y = 4.
	Составить уравнение касательной к окружности х² + у²–2х + 4у–13 = 0, проведенной в точке А(– 2; 1) на ней.
	Составить уравнение окружности, диаметром которой является общая хорда окружностей: х² + у² –4х –2у –15 = 0, х² + у² +6х +18у –55 = 0.
	Составить уравнение гиперболы с фокусами на оси Ox, если расстояние между ее фокусами равно 40, а уравнение ее асимптот y = ± .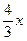
	Составить уравнение гиперболы с центром в начале координат и фокусами на оси Ox, проходящей через точки (− 6; − ), (6 ; 4).
	Составить уравнение кривой на плоскости, каждая точка которой равноудалена от прямой y = − 2 и от точки А(− 3; 4).
	Отрезок прямой 5x − 4y + 40 = 0, содержащийся между осями координат, служит диаметром окружности. Составить уравнение этой окружности.
	Составить уравнение эллипса с центром в начале координат и фокусами на оси Ox, проходящего через точки ( ; 2), (2; ).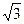
	Составить уравнение равносторонней гиперболы с фокусами на оси Oy, если гипербола проходит через точку (− ; − ).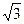
	Составить уравнение эллипса с центром в начале координат и фокусами на оси Ox, если он проходит через точки А(6; 4) и В(4; ).
	Составить уравнение директрисы параболы х² + 8х – 28у + 44 = 0.
	Составить уравнение окружности, проходящей через точку с координатами А(− 5; 6), и концентрической по отношению к окружности х² + у² – 2х + 6у – 87 = 0.
	Найти эксцентриситет эллипса .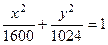
	Составить уравнение оси параболы х² + 2х – 20у – 79 = 0.
	Составить уравнение директрисы параболы у² – 4у + 8х – 12 = 0.
	Найти эксцентриситет гиперболы .

Справочный материал

к 6-й лабораторной работе

1. Кривые второго порядка: окружность, эллипс, гипербола и парабола.

2. Общее уравнение кривой второго порядка: А∙x²+В∙x∙y+С∙y²+D∙x+E∙y+F=0, где A, B, C, D, E, F – действительные числа, причем A + B + C > 0.

Примечание: не всякое уравнение А∙x²+В∙x∙y+С∙y²+D∙x+E∙y+F=0 представляет уравнение кривой второго порядка.

3. Окружность – множество всех точек плоскости, равноудаленных от данной точки (центра окружности).

4. 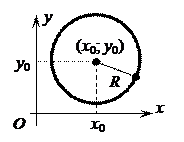Каноническое уравнение окружности

радиусаRуравнение окружности радиусаR

с центром в начале координат): x² + y² = R².

5. Уравнение окружности радиусаRс

центром в точке(x₀; y₀):

(x − x₀)² + (y − y₀)² = R².

6. Эллипс – множество всех точек M плоскости, сумма расстояний которых до двух данных точек (фокусов эллипса) есть величина постоянная, равная 2а, большая, чем расстояние между фокусами 2с: r₁ + r₂ = 2a > 2c > 0.

7. Каноническое уравнение эллипса: ,

где 0 < b < a, точки F₁(c; 0) и F₂(−c; 0) – фокусы эл-

липса; точки A₁(a; 0), A₂(− a; 0), B₁(b; 0), B₂(− b; 0) –

вершины эллипса, отрезок A₁A₂ длиной 2а – боль-

шая ось, отрезок В₁В₂ длиной 2b – малая ось эл-

липса; точка О(0; 0) – центр эллипса; длина отрезка

F₁F₂, равная 2с=2× , – фокусное расстояние.

8. Гипербола – множество всех точек М плоскости, абсолютная величина разности расстояний которых до двух данных точек (фокусов гиперболы) есть величина постоянная, равная 2а, меньшая, чем расстояние между фокусами 2с: |r₁ – r₂| = 2а < 2с.

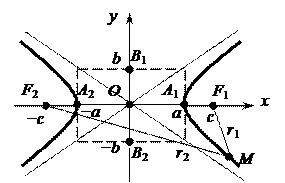9. Каноническое уравнение гиперболы:

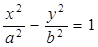, где точки F₁(c; 0) и F₂(−c; 0) –

фокусы гиперболы, точки A₁(a; 0), A₂(−a; 0)

– вершины гиперболы, точка О(0; 0) – центр

гиперболы,отрезок A₁A₂ длиной 2a – действи-

тельная ось, отрезок В₁В₂ длиной2b – мни-

мая ось гиперболы, длина отрезка F₁F₂, рав-

ная 2с,–фокусное расстояние,2c=2

прямые y = 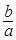×х, y = – 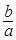×х − асимптоты гиперболы; a > 0, b > 0, c > 0. Если a = b, то гиперболаназывается равносторонней. Гиперболы и или называются сопряженными, они имеют общие асимптоты, ветви гиперболы находятся в верхнем и нижнем секторах этих пересекающихся асимптот и имеют вершины в точках В₁ и В₂, мнимая ось одной гиперболы является действительной для ей сопряженной и наоборот.

10. Парабола − множество всех точек М плоскости, равноудаленных от данной точки (фокуса параболы) и данной прямой (директрисы параболы).

11. Каноническое уравнение параболы:y²= 2px, где p – фокальный параметр параболы; точка О(0; 0) – вершина параболы; точка F(p/2; 0) – фокус параболы; прямая x=− p/2 – директриса (фокальный параметр р равен расстоянию от фокуса додиректрисы, p > 0); ось абсцисс – ось параболы.

12. Директриса кривой второго порядка(кроме окружности) – прямая, расстояние между которой и любой точкой M на кривой второго порядка пропорционально расстоянию между точкой M и соответствующим фокусом этой кривой.

Примечание: директриса и соответствующий ей фокус для эллипса и гиперболы лежат по одну сторону от центра этих кривых; у эллипса и гиперболы по две директрисы; у окружности нет директрис.Задание директрисы и соответствующего ей фокуса полностью определяет все параметры и расположение эллипса, гиперболы и параболы (для точек на ветвях гиперболы, чтобы не перегружать рисунок, указаны расстояния r и d только до фокуса F₁).

13. Эксцентриситет ε кривой второго порядка (кроме окружности) – отношение расстояния r от точки M до фокуса кривой второго порядка к расстоянию d от точки M до соответствующей этому фокусу директрисы, т.е. эксцентриситет ε= r/d. Для эллипса ε = r/d = c/a < 1; для гиперболы ε = r/d = c/a > 1; для параболы ε = r/d = 1; у окружности эксцентриситет равен 0.

14. Уравнения директрис кривых второго порядка: уравнения директрис эллипса и гиперболы: х = ± а/e = ± а²/с, где; уравнение директрисы параболы x = − p/2.

15. Если алгебраическое уравнениеА∙x²+В∙x∙y+С∙y²+D∙x+E∙y+F=0 задает кривую второго порядка, то тип этой кривой определяется значением определителяd= 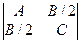:при d > 0 кривая 2-го порядка – эллипс (в случае А = С и В = 0 – окружность), при δ < 0 – гипербола, при δ = 0 – парабола.

16. Главные оси кривой второго порядка – координатные оси правой прямоугольной системы координат, в которой уравнение этой кривой является каноническим.