 |
Главная |
Лабораторная работа № 5. Прямая и плоскость
|
из
5.00
|
Прямая и плоскость
Теоретический минимум
1. Общее уравнение прямой на плоскости.
2. Уравнение прямой с угловым коэффициентом.
3. Уравнение прямой, проходящей через две точки.
4. Уравнение прямой в отрезках.
5. Полярное уравнение прямой.
6. Нормальное уравнение прямой.
7. Расстояние от точки до прямой на плоскости.
8. Угол между прямыми на плоскости.
9. Условие параллельности двух прямых.
10. Условие перпендикулярности двух прямых.
11. Уравнение плоскости, проходящей через данную точку, перпендикулярно заданному вектору.
12. Общее уравнение плоскости.
13. Уравнение плоскости, проходящей через три точки.
14. Уравнение плоскости в отрезках.
15. Нормальное уравнение плоскости.
16. Угол между двумя плоскостями.
17. Условие перпендикулярности двух плоскостей.
18. Условие параллельности двух плоскостей.
19. Расстояние от точки до плоскости.
20. Параметрические уравнения прямой в пространстве.
21. Канонические уравнения прямой в пространстве.
22. Общие уравнения прямой в пространстве.
23. Угол между прямыми в пространстве.
24. Угол между прямой и плоскостью.
Задания
1. Написать уравнения прямых, проходящих через точку М(х0; y0), одна из которых параллельна, а другая – перпендикулярна заданной прямой l. Выполнить чертеж.
| № | (х0; y0) | Уравнение прямой l | № | (х0; y0) | Уравнение прямой l |
| (– 2; 1) | 3x + 2y + 12 = 0 | (– 2; 2) | 4x + y – 3 = 0 | ||
| (2; – 1) | x – y + 1 = 0 | (3; – 1) | 3x – y + 2 = 0 | ||
| (3; – 3) | x + 2y – 4 = 0 | (– 2; 2) | x + 5y – 2 = 0 | ||
| (– 1; 4) | 2x – 5y + 2 = 0 | (1; – 5) | 3x + 3y + 2 = 0 | ||
| (– 5; 0) | – x + 2y + 9 = 0 | (2; – 3) | – 2x + 5y – 4 = 0 | ||
| (4; – 1) | x + 4y – 3 = 0 | (– 3; – 4) | x – 3y – 5 = 0 | ||
| (1; – 1) | 2x + 2y + 1 = 0 | (5; 1) | – 2x + 5y – 2 = 0 | ||
| (2; 0) | – 4x + y + 2 = 0 | (– 2; 4) | 4x + 2y + 12 = 0 | ||
| (6; – 1) | 2x – 3y + 4 = 0 | (1; 6) | – 2x + y = 0 | ||
| (1; – 3) | – 3x – y + 2 = 0 | (0; – 3) | 2x – 5y + 21 = 0 | ||
| (1; 1) | x – y + 10 = 0 | (2; 4) | – x – 5y – 12 = 0 | ||
| (3; – 2) | 2x – 3y – 2 = 0 | (– 4; 4) | x + 5y + 13 = 0 | ||
| (– 1; 1) | x + y + 12 = 0 | (– 3; 0) | 4x – y + 13 = 0 | ||
| (2; 2) | 3x + y + 4 = 0 | (3; 3) | – 4x + y – 2 = 0 | ||
| (2; 1) | x + 4y + 1 = 0 | (1; 4) | – 2x + 5y – 2 = 0 |
2. Написать уравнения прямой, которая проходит через точку М(х0; y0)и через точку пересечения прямых l1 и l2. Выполнить чертеж.
| № | (х0; y0) | Уравнения прямых l1 и l2 | № | (х0; y0) | Уравнения прямых l1 и l2 |
| (1; – 2) | l1: 2x – y – 1 = 0 l2: x – y – 1 = 0 | (3; – 2) | l1: x – 2y + 3 = 0 l2: 3x – y – 1 = 0 | ||
| (– 4; 0) | l1: x + y – 2 = 0 l2: x – 3y + 2 = 0 | (0; 1) | l1: x + 3y – 7 = 0 l2: – x + y – 1 = 0 | ||
| (1; – 1) | l1: 7x – 2y – 5 = 0 l2: x – 5y + 4 = 0 | (1; 0) | l1: 4x – y – 5 = 0 l2: x + 2y – 8 = 0 | ||
| (4; 3) | l1: 5x – 2y – 1 = 0 l2: 2x – 3y + 4 = 0 | (– 1; – 4) | l1: 2x – y – 5 = 0 l2: x + y + 7 = 0 | ||
| (3; 3) | l1: x – 2y – 1 = 0 l2: x – 7y + 4 = 0 | (2; – 4) | l1: 3x – y + 10 = 0 l2: – x – y – 2 = 0 | ||
| (4; 4) | l1: 2x + 2y – 2 = 0 l2: x – 3y + 5 = 0 | (2; – 5) | 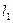 : 3x – 4y – 5 = 0
l2: 4x + 3y – 15 = 0 : 3x – 4y – 5 = 0
l2: 4x + 3y – 15 = 0
| ||
| (0; – 3) | 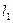 : x + 4y – 3 = 0 : x + 4y – 3 = 0
 : x + 5y + 4 = 0 : x + 5y + 4 = 0
| (2; 1) | l1: – 2x + y – 1 = 0
 : 2y + 1 = 0 : 2y + 1 = 0
| ||
| (2; – 2) | l1: 3x + 2y – 1 = 0 l2: x – 3y – 4 = 0 | (1; – 4) | l1: – 2x + 2y – 11 = 0 l2: 2x + 3 = 0 | ||
| (– 2; 0) | l1: 2x + 3y + 5 = 0 l2: – x + 4y + 3 = 0 | (– 2; 4) | l1: – x + 2y – 1 = 0 l2: – 7x – 4y + 11 = 0 | ||
| (1; – 2) | l1: 2x + y + 6 = 0 l2: 3x + 5y – 15 = 0 | (2; 3) | l1: – x + y – 4 = 0 l2: – 7x – 4y – 6 = 0 | ||
| (2; 1) | l1: 2x – y + 3 = 0 l2: 3x + 5y + 11 = 0 | (1; – 4) | l1: 3x – 2y – 8 = 0 l2: – 3x + 4y + 4 = 0 | ||
| (– 1; – 3) | l1: 3x + 2y – 5 = 0 l2: x – 2y + 1 = 0 | (3; 2) | l1: – 3x + 4y + 1 = 0 l2: 7x – 9y – 3 = 0 | ||
| (– 1; 1) | l1: 3x + 2y – 5 = 0 l2: x – 2y + 1 = 0 | (– 3; 3) | l1: – 3x + 4y + 14 = 0 l2: 7x – 4y – 6 = 0 | ||
| (2; – 3) | l1: x + y – 2 = 0 l2: x – 2y – 1 = 0 | (1; 7) | l1: – 2x + 5y + 9 = 0 l2: 3x – 4y – 6 = 0 | ||
| (4; 0) | l1: x + 2y – 5 = 0 l2: x – 2y + 2 = 0 | (– 1; 5) | l1: 5x + 3y – 1 = 0 l2: 4x + 5y + 7 = 0 |
3. Найти расстояние от точки Р(х0; y0) до прямой l:
| № | (х0; y0) | Уравнение прямой l | № | (х0; y0) | Уравнение прямой l |
| (2; 2) | 
| (–2; 1) | 
| ||
| (–2; 2) | 
| (3; –2) | 
| ||
| (2; 3) | 
| (–3; 0) | 
| ||
| (3; 2) | 
| (–2; 1) | 
| ||
| (2; 4) | 
| (0; –1) | 
| ||
| (–1; –1) | 
| (0; 2) | 
| ||
| (3; –1) | 
| (1; –4) | 
| ||
| (1; 1) | 
| (–2; 0) | 
| ||
| (–2; 1) | 
| (1; 2) | 
| ||
| (–3; 1) | 
| (1; –2) | 
| ||
| (–1; 3) | 
| (–2; 1) | 
| ||
| (–1; –2) | 
| (–3; 1) | 
| ||
| (1; 1) | 
| (2; 3) | 
| ||
| (3; 1) | 
| (–2; 1) | 
| ||
| (–3; 1) | 
| (3; 4) | 
|
3. Даны координаты вершин пирамиды ABCD.
Составить:
1) канонические уравнения прямой AB;
2) общее уравнение плоскости ABC;
3) канонические уравнения высоты DO,проведенной из вершины D на основание ABC.
Найти:
4) угол между ребром AD и гранью ABC;
5) длину высоты DO.
| № | A | B | C | D |
| (4; 2; 5) | (0; 7; 2) | (0; 2; 7) | (1; 5; 0) | |
| (4; 4; 10) | (4; 10; 2) | (2; 8; 4) | (9; 6; 4) | |
| (4; 6; 5) | (6; 9; 4) | (2; 10; 10) | (7; 5; 9) | |
| (3; 5; 4) | (8; 7; 4) | (5; 10; 4) | (4; 7; 8) | |
| (10; 6; 6) | (– 2; 8; 2) | (6; 8; 9) | (7; 10; 3) | |
| (1; 8; 2) | (5; 2; 6) | (5; 7; 4) | (4; 10; 9) | |
| (6; 6; 5) | (4; 9; 5) | (4; 6; 11) | (6; 9; 3) | |
| (7; 2; 2) | (5; 7; 7) | (5; 3; 1) | (2; 3; 7) | |
| (8; 6; 4) | (10; 5; 5) | (5; 6; 8) | (8; 10; 7) | |
| (7; 7; 3) | (6; 5; 8) | (3; 5; 8) | (8; 4; 1) | |
| (8; 4; 10) | (0; 14; 4) | (0; 4; 14) | (2; 10; 0) | |
| (8; 8; 20) | (8; 20; 4) | (4; 16; 8) | (18; 12; 8) | |
| (8; 12; 10) | (12; 18; 8) | (4; 20; 20) | (14; 10; 18) | |
| (6; 10; 8) | (16; 14; 8) | (10; 20; 8) | (8; 14; 16) | |
| (20; 12; 12) | (– 4; 16; 4) | (12; 16; 18) | (14; 20; 6) | |
| (2; 16; 4) | (10; 4; 12) | (10; 14; 8) | (8; 20; 18) | |
| (12; 12; 10) | (8; 18; 10) | (8; 12; 22) | (12; 18; 10) | |
| (14; 4; 4) | (10; 14; 14) | (10; 6; 14) | (4; 6; 14) | |
| (16; 12; 8) | (20; 10; 10) | (10; 12; 14) | (16; 20; 14) | |
| (14; 14; 6) | (12; 10; 16) | (6; 10; 16) | (16; 8; 2) | |
| (5; 2; 4) | (2; 7; 0) | (7; 2; 0) | (0; 5; 1) | |
| (10; 4; 4) | (2; 10; 4) | (4; 8; 2) | (4; 6; 9) | |
| (5; 6; 4) | (4; 9; 6) | (10; 10; 2) | (9; 5; 7) | |
| (4; 5; 3) | (4; 7; 8) | (4; 10; 5) | (8; 7; 4) | |
| (6; 6; 10) | (2; 8; – 2) | (9; 8; 6) | (3; 10; 7) | |
| (2; 8; 1) | (6; 2; 5) | (4; 7; 5) | (9; 10; 4) | |
| (5; 6; 6) | (5; 9; 4) | (11; 6; 4) | (3; 9; 6) | |
| (2; 2; 7) | (7; 7; 5) | (1; 3; 2) | (7; 3; 2) | |
| (4; 6; 8) | (5; 5; 10) | (8; 6; 5) | (7; 10; 8) | |
| (3; 7; 7) | (8; 5; 6) | (8; 5; 3) | (1; 4; 8) |
Справочный материал
к 5-й лабораторной работе
1. Уравнения прямой на плоскости:
Ø общее уравнение прямойl: Ax + By + C = 0, где A, B, С – числа, A2 + B2 ¹ 0; нормальный вектор прямой N = {A; B} ^ l; направляющий вектор прямой а= {B; – A} || l; N ^ l;
Ø уравнение прямой, проходящей через точкуМ(x0;y0)перпендикулярно вектору N = {A; B}: A(x – х0) + B(y – y0)= 0;
Ø уравнение прямой, проходящей через точкуМ(x0;y0) с заданным направляющим вектором a = {ax; ay}(каноническое уравнение прямой):  ;
;
Ø уравнение прямой, проходящей через две точки М1(x1; y1) и М2(x2; y2) при x1 ¹ x2 и y1 ¹ y2:
 или
или  = 0
= 0
(при x1 = x2 и y1 ¹ y2 уравнение прямой имеет вид x = x1, а при y1 = y2 и x1 ¹ x2 – вид y = y1);
Ø уравнение прямой с угловым коэффициентом k = tg j , где j – угол между прямой и положительным направлением оси х, отсчитываемый от этой оси против часовой стрелки: y = k×x + b, число b – ордината точки пересечения прямой с координатной осью y;
Ø уравнение прямой с угловым коэффициентомk, проходящей через точку М(x0; y0):
y – y0= k×(x – x0);
Ø 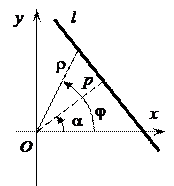 уравнение прямой в отрезках, не проходящей через начало координат:
уравнение прямой в отрезках, не проходящей через начало координат:  , где а – абсцисса точки пересечения прямой с координатной осью х, b – ордината точки пересечения прямой с координатной осью y;
, где а – абсцисса точки пересечения прямой с координатной осью х, b – ордината точки пересечения прямой с координатной осью y;
Ø нормальное уравнение прямой:х×cos a + y×sin a – p = 0,
где p – расстояние от начала координат до прямой, a – угол
между осью Ох и перпендикуляром к прямой из начала коор-
динат (длиной р ³ 0); чтобы составить нормальное уравнение
прямой, заданной общим уравнением Ax + By + C = 0, доста-
точно разделить данное уравнение на  , причем верх-
, причем верх-
ний знак берется, когда С > 0, а нижний – когда С < 0; если же
С = 0, то выбор знака не имеет значения;
Ø полярное уравнение прямой: r(j)= р/cos(j – a), где р ¹ 0;
Ø параметрические уравнения прямой с направляющим вектором a = {ax; ay}, проходящей через точку М(x0; y0): 
2. Расстояние от точкиР(x0; y0)до прямойAx + By + C = 0(т.е. длина перпендикуляра, опущенного из точки Р(x0; y0) на прямую):  .
.
3.Косинус острого угла a между прямымиA1x + B1y + C1= 0иA2x + B2y + C2= 0на плоскости (угол между векторами N1 = {A1; B1} и N2 = {A2; B2}):  .
.
4. Уравнения плоскости:
Ø общее уравнение плоскости:Ax + By + Cz + D = 0, где A, B, С, D –числа, A2 + B2 + С2 ¹ 0; нормальный вектор плоскости N = {A; B; С} ^ плоскости;
Ø уравнение плоскости, проходящей через точку М(x0; y0; z0) перпендикулярно вектору N = {A; B; С}: A×(x – х0) + B×(y – y0) + С×(z – z0) = 0;
Ø уравнение плоскости в отрезках – уравнение плоскости, не проходящей через начало координат:  , где а – абсцисса точки пересечения плоскости с координатной осью х, b – ордината точки пересечения плоскости с координатной осью y, с – аппликататочки пересечения плоскости с координатной осью z;
, где а – абсцисса точки пересечения плоскости с координатной осью х, b – ордината точки пересечения плоскости с координатной осью y, с – аппликататочки пересечения плоскости с координатной осью z;
Ø уравнение плоскости, проходящей через три точки М1(x1; y1; z1), М2(x2; y2; z2) и М3(x3; y3; z3), не лежащих на одной прямой:  = 0;
= 0;
Ø нормальное уравнение плоскости:x×cos a + y×cos b+ z×cos g – p = 0, где cos a, cos b, cos g – направляющие косинусы нормального вектора плоскости N = {A; B; С}, исходящего из начала координат, т.е. косинусы углов между указанным вектором N и положительными направлениями координатных осей x, y, z соответственно; чтобы найти нормальное уравнение плоскости, заданной общим уравнением Ax + By + Cz + D = 0, достаточно разделить данное уравнение на  , причем верхний знак берется, когда D > 0, а нижний – когда D < 0; если же D = 0, то выбор знака не имеет значения.
, причем верхний знак берется, когда D > 0, а нижний – когда D < 0; если же D = 0, то выбор знака не имеет значения.
| Уравнение плоскости Q | Ориентация плоскости Q в пространстве |
| Ax + By + Cz = 0 | плоскость Q проходит через начало координат |
| By + Cz + D = 0 | плоскость Q параллельна координатной оси х |
| Ax + Cz + D = 0 | плоскость Q параллельна координатной оси y |
| Ax + By + D = 0 | плоскость Q параллельна координатной оси z |
| x = a | плоскость Q ^оси х (т.е.параллельна координатной плоскости yz)и пересекает ось x в точке x = a |
| y = b | плоскость Q ^оси у (т.е.параллельна координатной плоскости xz)и пересекает ось y в точке y = b |
| z = с | плоскость Q ^оси z (т.е.параллельна координатной плоскости xy)и пересекает ось z в точке z = с |
| x = 0 | плоскость Q – координатная плоскость yz |
| y = 0 | плоскость Q – координатная плоскость xz |
| z = 0 | плоскость Q – координатная плоскость xy |
5. Расстояние от точкиР(x0; y0; z0)до плоскости Ax + By + Cz + D = 0:  .
.
6. Косинус острого угла j между плоскостямиA1x + B1y + C1z + D1 = 0и A2x + B2y + C2z + D2 = 0:
 ,
,
где N1 = {A1; B1; С1} и N2 = {A2; B2; С2} – нормальные векторы 1-й и 2-й плоскости, соответственно.
7. Уравнения прямой в пространстве:
Ø общие уравнения прямой в пространстве (уравнения прямой как линии пересечения двух непараллельных плоскостей) A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2= 0: 
направляющий вектор этой прямой а = N1´N2 =  , а точка на прямой определяется решением системы при фиксированном значении одной из переменных, например, при z0 = 0 значения x0, y0 являются решением системы
, а точка на прямой определяется решением системы при фиксированном значении одной из переменных, например, при z0 = 0 значения x0, y0 являются решением системы 
Ø канонические уравнения прямой – уравнения прямой, проходящей через точку М(x0; y0; z0), с заданным направляющим вектором a = {ax; ay; az}:  ;
;
Ø уравнения прямой, проходящей через две точки М1(x1; y1; z1), М2(x2; y2; z2):  ;
;
Ø параметрические уравнения прямой, проходящей через точку М(x0; y0; z0), с заданным направляющим вектором a = {ax; ay; az}: х = х0 +t·ax; y = y0 +t·ay; z = z0 + t·az.
8. Угол между прямой и плоскостью – острый угол qмежду прямой и ее проекцией на плоскость; если прямая задана каноническими уравнениями  , а плоскость – общим уравнением Ax + By + Cz + D = 0, то sin q =
, а плоскость – общим уравнением Ax + By + Cz + D = 0, то sin q =  , где N = {A; B; С} – нормальный вектор плоскости, a = {ax; ay; az} – направляющий вектор прямой.
, где N = {A; B; С} – нормальный вектор плоскости, a = {ax; ay; az} – направляющий вектор прямой.
9. Угол между двумя прямыми в пространстве: если известны направляющие векторы a1 и a2 двух прямых в пространстве соответственно, то косинус острого угла a между этими прямыми:
cos a=  .
.
|
из
5.00
|
Обсуждение в статье: Лабораторная работа № 5. Прямая и плоскость |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

