Математические модели сложных измерительных сигналов

В средствах измерений используется большое число измерительных сигналов, имеющих самые раз­нообразные формы. Рассмотрим некоторые из них, наиболее часто встречающиеся на практике.

Прямоугольные импульсы. Одиночный идеальный прямоугольный импульс (рис. 2.6, а) описывается уравнением

(3.28)

т.е. он формируется как разность двух единичных функций, сдвинутых во времени на величину — дли­тельность импульса.

Последовательность прямоугольных импульсов есть сумма одиночных импульсов:

Для ее описания необходимо знать три параметра: амплитуду , длительность и период 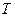(рис. 3.6, б). Отношение периода к длительности прямоугольного импульса называется скважностью, а обратная вели­чина — коэффициентом заполнения. При скважности, равной двум, последовательность импульсов называ­ют меандром (см. рис. 2.6, б).

Идеальные прямоугольные импульсы в природе не встречаются. В реальных импульсах время измене­ния сигнала от нулевых до амплитудных значений (и обратно) всегда имеет конечную длительность, т.е. фронт и спад 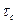(рис. 3.6, в). Следовательно, у ре­альных импульсов форма близка к трапецеидальной.

Трапецеидальный импульс также является идеа­лизации реальных импульсов, которые имеют гораздо более сложную форму. Она отличается от трапеции спадом вершины импульса, выбросами на вершине и в паузе и другими особенностями, учтенными в сис­теме параметров реального прямоугольного импульса по ГОСТ 16465-70.

Рис. 3.6. а) – формирование идеального прямоугольного импульса; б) – последовательность прямоугольных импульсов; в) – последовательность трапецеидальный импульс

Модулированные сигналы. Модулированным назы­вается сигнал, являющийся результатом взаимодей­ствия двух или более сигналов, т.е. модуляции. Мо­дуляция — это воздействие измерительного сигнала на какой-либо параметр стационарного сигнала 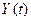, обладающего такими физической природой и характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала, именуемого не­сущим, обычно выбирают синусоидальное (гармони­ческое) колебание или последовательность импуль­сов.

Амплитудно-модулированные сигналы описываются формулой:

(3.30)

Физический процесс, обратный модуляции, на­зывается демодуляцией, или детектированием, и за­ключается в получении из модулированного сигнала другого сигнала, пропорционального модулирующе­му. Задача демодуляции — по возможности полное восстановление информации, содержащейся в моду­лирующем сигнале .

Вид модуляции и способ детектирования зависят от требований, предъявляемых к точности передачи информации. Наиболее простым модулированным гармоническим сигналом является амплитудно-модулированный сигнал, в котором измерительная информа­ция содержится в амплитуде несущего синусоидаль­ного сигнала (рис. 3.7).

Амплитудно-модулированные сигналы описыва­ются формулой

где m — глубина амплитудной модуляции (всегда мень­ше единицы).

При частотной модуляции измеритель­ная информация содержится в частоте модулирован­ного сигнала, т. е.

(3.31)

где — наибольшее изменение частоты модулиро­ванного сигнала, т.е. девиация частоты, пропорцио­нальная амплитуде модулирующего сигнала.

При фазовой модуляции модулирующий сигнал X(t) воздействует на фазу несущего колебания:

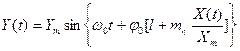, (3.32)

где m_ф коэффициент фазовой модуляции.

Для того чтобы при детектировании можно было восстановить модулирующий сигнал, необходимо иметь сигнал вида (2.7), называемый опорным. Отно­сительно него наблюдают, как меняется фаза модули­рованного сигнала.

Если модулируемым сигналом является периоди­ческая последовательность прямоугольных импуль­сов, то возможны три вида модуляции (рис. 3.8): ам­плитудно-импульсная (АИМ); частотно-импульсная (ЧИМ); широтно-импульсная (ШИМ).

При этом параметром, несущим измерительную информацию, соответственно являются амплитуда, частота и длительность импульсов.

Рис. 3.8. Несущая последовательность прямоугольных импульсов (a), модулирующий {б}, амплитудно-модулированный (в), частотно-модулированный (г) и широтно-модулированный (д) сигналы