 |
Главная |
Квантование и дискретизация измерительных сигналов
|
из
5.00
|
По характеру изменения информативного параметра сигналы делятся на четыре группы;
1. Сигналы, непрерывные по времени и размеру, — наиболее распространенные (см. рис. 3.2, а, 3.9). Они чаще всего встречаются в практике измерений, поскольку все первичные природные сигналы макромира непрерывны по времени и размеру. Такие сигналы определены в любой момент времени существования сигнала и могут принимать любые значения в диапазоне его изменения.
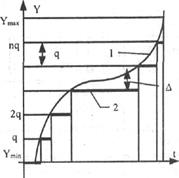
Рис. 3.9. Исходный непрерывный
сигнал (1) и сигнал непрерывный по времени и квантованный по размеру (2}
Сигналы, непрерывные по времени и квантованные по размеру, получаются из сигнала, непрерывного по времени и размеру, посредством его квантования.
Квантование — измерительное преобразование непрерывно изменяющейся величины в ступенчато изменяющуюся с заданным размером ступени q — квантом. В результате проведения этой операции непрерывное множество значений сигнала Y(t) в диапазоне от Ymin до Ymax преобразуется в дискретное множество значений YM(t) Квантование широко применяется в измерительной технике. Существует большая группа естественно квантованных физических величин. К ним относятся электрический заряд, квантом которого является заряд электрона, масса тела, квантом которой является масса молекулы или атома, составляющих данное тело, и др.
Процесс квантования описывается уравнением
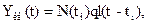 (3.33)
(3.33)
где N(ti) — число квантов; l(t-ti) — единичная функция,
Любой процесс измерения по сути своей есть процесс квантования. Например, при измерении длины тела линейкой с миллиметровыми делениями определяется целое число миллиметров, наиболее близкое к истинному размеру тела. В данном случае в роли кванта выступает миллиметр. При использовании микрометра квантом является величина, равная 1СГ6м.
Погрешность квантования∆ — методическая погрешность отражения непрерывной величины ограниченным по числу разрядов числом. Она равна разности между значением непрерывной функции и значением, полученным в результате квантования;
Погрешность квантования подчиняется равномерному, закону распределения с основанием, равным q. Ее СКО при всех видах равномерного квантования σ(∆)=q/(2√3).
Сигналы, дискретизированные по времени и непрерывные по размеру, получаются из непрерывных по времени и размеру сигналов посредством дискретизации. Дискретизация— измерительное преобразование непрерывного во времени сигнала 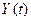 в последовательность мгновенных значений этого сигнала
в последовательность мгновенных значений этого сигнала 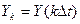 ,соответствующих моментам времени
,соответствующих моментам времени 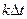 ,где
,где 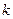 = 1, 2... Интервал времени
= 1, 2... Интервал времени 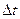 называется шагом дискретизации, а обратная ему величина
называется шагом дискретизации, а обратная ему величина 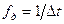 – частотой дискретизации.
– частотой дискретизации.
Процесс дискретизации непрерывного сигнала показан на рисунке
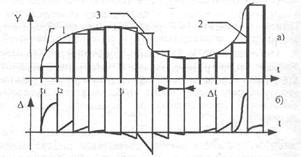
Рис. 3.10. Дискретизация непрерывного сигнала (а): исходный непрерывный сигнал (1), сигнал, дискретизированный по времени и непрерывный по размеру (2), и восстановленный при помощи полинома Лагрэкжа нулевой степени непрерывный во времени сигнал (3) и погрешность восстановления (б)
Математически он описывается с помощью дельта функции 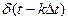 , которая, как известно, обладает стробирующим действием. Идеальный дискретизированный сигнал
, которая, как известно, обладает стробирующим действием. Идеальный дискретизированный сигнал 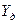 является последовательностью импульсов нулевой длительности и аналитически может быть представлен в виде
является последовательностью импульсов нулевой длительности и аналитически может быть представлен в виде
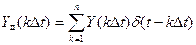 (3.34)
(3.34)
где Y(k∆t) — значение непрерывного сигнала в каждой точке дискретизации.
Дискретизация бывает равномерной 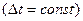 и неравномерной(
и неравномерной( 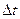 — переменная величина). Частота дискретизации выбирается на основе априорных сведений о характеристиках дискретизируемого сигнала. На практике наибольшее распространение получила равномерная дискретизация. Это объясняется тем, что алгоритмы дискретизации и последующего восстановления сигнала и реализующая их аппаратура относительно просты. Однако при недостаточности априорных данных о характеристиках сигнала возможна значительная избыточность отсчетов.
— переменная величина). Частота дискретизации выбирается на основе априорных сведений о характеристиках дискретизируемого сигнала. На практике наибольшее распространение получила равномерная дискретизация. Это объясняется тем, что алгоритмы дискретизации и последующего восстановления сигнала и реализующая их аппаратура относительно просты. Однако при недостаточности априорных данных о характеристиках сигнала возможна значительная избыточность отсчетов.
В дискретизированном сигнале отсутствуют промежуточные значения, которые содержались в исходном непрерывном сигнале. Однако часто принципиально необходим непрерывный сигнал. Поэтому во многих случаях дискретизированный сигнал требуется преобразовать в непрерывный, т. е. восстановить его промежуточные значения. Задача восстановления дискретизированных сигналов в общем случае аналогична задаче интерполирования функций. При восстановлении исходного сигнала 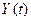 по совокупности выборок
по совокупности выборок 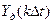 формируется обобщенный многочлен
формируется обобщенный многочлен
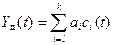 (3.35)
(3.35)
где 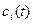 — система базисных функций, которая обычно является ортогональной или ортонормированной;
— система базисных функций, которая обычно является ортогональной или ортонормированной; 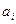 — коэффициенты ряда. Его значения в точках дискретизации совпадают со значениями непрерывной функции. В ряде случаев при формировании восстанавливающего многочлена накладывается условие совпадения производных до заданного порядка п включительно.
— коэффициенты ряда. Его значения в точках дискретизации совпадают со значениями непрерывной функции. В ряде случаев при формировании восстанавливающего многочлена накладывается условие совпадения производных до заданного порядка п включительно.
При восстановлении непрерывный сигнал на каждом из участков между соседними дискретными значениями заменяется кривой, вид которой определяется выбранными базисными функциями. Восстановление непрерывного сигнала из дискретизированного должно проводиться с возможно меньшей заданной погрешностью. Для этого необходимо соответствующим образом выбрать для данного участка сигнала восстанавливающую базисную функцию.
Коэффициенты ряда и базисные функции могут выбираться на основе различных критериев, например: наибольшего отклонения, минимума погрешности или совпадения значений восстанавливаемого непрерывного сигнала с мгновенными значениями дискретизированного сигнала. В измерительной технике наиболее широко используется последний критерий, так как он удобен для аналитического восстановления с помощью компьютера на основе результатов измерения мгновенных значений дискретизированного сигнала, отличается простотой реализации и достаточно высокой точностью.
Восстановление сигнала в данном случае регулируется теоремой Котельникова, которая формулируется следующим образом: если функция Y(t), удовлетворяющая условиям Дирихле — ограничена, кусочно-непрерывна, имеет конечное число экстремумов — и обладающая спектром с граничной частотой 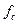 , дискретизирована циклически с периодом
, дискретизирована циклически с периодом 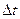 , меньшим или равным
, меньшим или равным 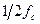 т. е.
т. е. 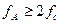 , то она может быть восстановлена по всей этой совокупности ее мгновенных значений без погрешности.
, то она может быть восстановлена по всей этой совокупности ее мгновенных значений без погрешности.
Если теорема Котельникова выполняется, то непрерывный сигнал 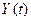 может быть восстановлен как сумма базисных функций — рядом Котельникова:
может быть восстановлен как сумма базисных функций — рядом Котельникова:
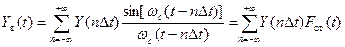 (3.36)
(3.36)
где 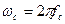 — круговая граничная частота спектра непрерывного сигнала
— круговая граничная частота спектра непрерывного сигнала 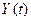 ;
; 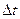 — период дискретизации;
— период дискретизации; 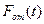 - функция отсчетов.
- функция отсчетов.
Ряд Котельникова является одним из примеров обобщенного ряда Фурье и замечателен тем, что его коэффициенты равны мгновенным дискретизированным значениям сигнала 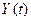 и поэтому определяются наиболее простым способом.
и поэтому определяются наиболее простым способом.
Погрешность восстановления дискретизированных сигналов равна разности между значениями непрерывной исходной функции и восстанавливающей функции. Она существенным образом зависит от вида используемой базисной функции.
Погрешность восстановления зависит от закона изменения дискретизируемой функции, выбранных восстанавливающих полиномов и величины шага или частоты дискретизации. Чем менее гладкой и монотонной является дискретизируемая функция (т. е, чем больше в ее спектральном составе высших гармоник), тем больше, при прочих равных условиях, погрешность восстановления.
Погрешность восстановления доводят до требуемой величины главным образом соответствующим выбором шага дискретизации. Очевидно, что при его уменьшении погрешность восстановления снижается.
Методика расчета зависит от применяемых базисных функций. При использовании ряда Котельникова частота дискретизации рассчитывается по формуле 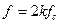 , где
, где 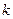 — коэффициент запаса, выбираемый из диапазона (1,5—6) и учитывающий неограниченность спектра реальных сигналов;
— коэффициент запаса, выбираемый из диапазона (1,5—6) и учитывающий неограниченность спектра реальных сигналов; 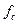 — максимальная частота в спектре сигнала.
— максимальная частота в спектре сигнала.
Сигналы, дискретизированные по времени и квантованные по размеру, согласно приведенной классификации являются цифровым сигналами. На практике они формируются цифроаналоговыми преобразователями. Последние фактически являются управляемыми цифровым кодом мерами, выходной сигнал которых подвергнут дискретизации. Следовательно, в этих устройствах параллельно осуществляются два процесса преобразования измерительной информации: дискретизация и квантование. Их совместное действие описывается математическим выражением
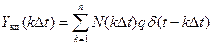 (3.37)
(3.37)
где 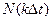 — цифровой код (число квантов), соответствующий моменту
— цифровой код (число квантов), соответствующий моменту 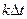 .
.
. 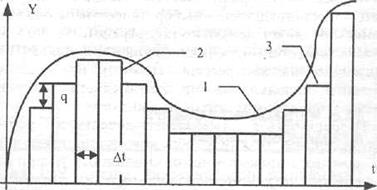
Рис. 3.11. Исходный непрерывный сигнал (1), сигнал,дискретизированный по времени и квантованный по уровню (2),
и восстановленный непрерывный сигнал (3)
Значения сигнала, дискретизированного по времени и квантованного по уровню, определены только в моменты, кратные периоду дискретизации ∆t. Поэтому имеет место задача формирования непрерывного сигнала по данным значениям. Эта задача аналогична рассмотренной задаче восстановления дискретизированного сигнала. Отличие состоит в том, что последний равен исходному непрерывному сигналу, а квантованный и дискретизированный сигналы отличаются от него, но не более чем на величину кванта q. Вследствие этого погрешность состоит из двух составляющих, обусловленных процессами дискретизации и квантования.
|
из
5.00
|
Обсуждение в статье: Квантование и дискретизация измерительных сигналов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

