 |
Главная |
СПЕКТРАЛЬНЫЙ И КОРЕЛЛЯЦИОННЫЕ АНАЛИЗ СЛУЧАЙНОГО ПРОЦЕССА. ТЕОРЕМА ХИНЧЕНА–ВИННЕРА
|
из
5.00
|
В отличие от детерминированных сигналов, формы которых мы знаем точно, мгновенные значения случайных сигналов заранее не известны и могут быть представлены лишь с некоторой вероятностью меньше единицы. Характеристики таких сигналов являются статистическими, т.е. имеют вероятностный вид. В информационных технологиях существуют два основных класса сигналов, нуждающихся в вероятностных описаниях. Во-первых, это шумы (помехи) – хаотически изменяющиеся во времени параметры какого-либо процесса. Во-вторых, случайными являются все сигналы несущие информацию. Поэтому для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.
Ансамбль реализаций
Математическая модель изменяющегося во времени случайного сигнала называется случайным процессом. По определению случайный процесс X(t) – это функция особого вида, характеризующаяся тем, что значения, принимаемые ею, в любой момент времени 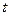 , являются случайной величиной. В технической литературе случайный сигнал и случайный процесс понимаются как синонимы.
, являются случайной величиной. В технической литературе случайный сигнал и случайный процесс понимаются как синонимы.
До регистрации (до приема) случайного сигнала, его рассматривают как случайный процесс, представляющий собой совокупность (ансамбль) функций времени  , подчиняющаяся некоторой общей для них статистической закономерности. Одна из этих функций
, подчиняющаяся некоторой общей для них статистической закономерности. Одна из этих функций  ставшая полностью известной после приема и обработки сообщения называется реализацией случайного процесса. Эта реализация является не случайной, а детерминированной функцией времени.
ставшая полностью известной после приема и обработки сообщения называется реализацией случайного процесса. Эта реализация является не случайной, а детерминированной функцией времени.
Для анализа свойств и характеристик случайного процесса, а также для различных его преобразований нужно знать его математическую модель.
В качестве примера случайного процесса можно использовать модель, представляющую собой гармонические колебания с детерминированными амплитудой и частотой, но со случайной начальной фазой
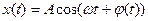
на рис.5.1. представлена эта реализация с дискретными значениями  .
.
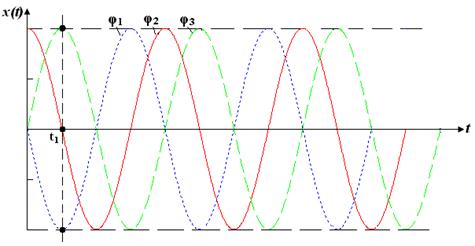
Рис.5.1.Реализация гармонического сигнала со случайной начальной фазой.
 –ансамбль реализаций процесса
–ансамбль реализаций процесса 
Хотя начальная фаза  случайная, но мы знаем, что она распределена в интервале 0-2π. Если она распределена равномерно на этом интервале, то плотность вероятности проявления того или иного значения начальной фазы
случайная, но мы знаем, что она распределена в интервале 0-2π. Если она распределена равномерно на этом интервале, то плотность вероятности проявления того или иного значения начальной фазы

Случайные процессы, конкретный вид реализаций которых определяется значениями конечного числа параметров (случайных величин) называются квазидетерминированными.
В любом случайном процессе, заданном n - параметрами ансамбля реализаций  , i=1,n выбирается произвольный момент времени
, i=1,n выбирается произвольный момент времени 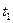 , в котором фиксируются все значения, принимаемых всеми реализациями
, в котором фиксируются все значения, принимаемых всеми реализациями 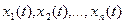 . Совокупность этих значений, как было указано, образует одномерное сечение случайного процесса и представляют собой случайную величину
. Совокупность этих значений, как было указано, образует одномерное сечение случайного процесса и представляют собой случайную величину  .
.
Описание случайных процессов, как известно, возможно с помощью следующих операторов.
 -математическое ожидание (среднее отклонение),
-математическое ожидание (среднее отклонение),
 - среднеквадратическое отклонение,
- среднеквадратическое отклонение,
 - дисперсия (флуктуация отклонения от математического ожидания).
- дисперсия (флуктуация отклонения от математического ожидания).
Дисперсия характеризует среднюю мощность отклонения случайного процесса от его математического ожидания, т. е. его среднее отклонение. Среднеквадратическое отклонение служит амплитудной мерой разброса случайного процесса в момент времени 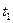 относительно математического ожидания.
относительно математического ожидания.
В нашем случае можно выделить два вида распределения случайной величины : это равномерное (модель шума) и нормальное (модель сигнала). Рис.5.2.
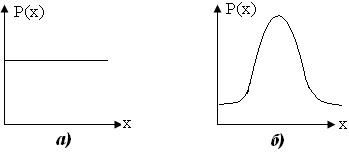
Рис.5.2. Плотность вероятности случайной величины при а) равномерном распределении, б) нормальном распределении
Широкое распространение нормального распределения в природе объясняется тем, что при суммировании достаточно большого числа равномощных статистических независимых случайных величин, имеющих произвольные плотности распределения вероятности, плотность распределения стремится к нормальной. Это положение носит название центральной предельной теоремы.
Весьма полезным для математического анализа свойств нормального распределения является то, что из некоррелированности гауссовых случайных величин следует их статистическая независимость.
Одномерная плотность вероятности и связанные с ней числовые характеристики позволяют получить важную информацию. Однако для решения многих задач информационных технологий таких сведений не достаточно, т. к. они дают вероятностное представление о случайном процессе  только в отдельные моменты времени
только в отдельные моменты времени  и не дают информацию об их изменении во времени.
и не дают информацию об их изменении во времени.
Для описания временных характеристик  необходимо использовать корреляционную функцию или привлечь для этого спектральные характеристики случайного процесса.
необходимо использовать корреляционную функцию или привлечь для этого спектральные характеристики случайного процесса.
Сначала рассмотрим корреляционный анализ детерминированных
функций дающих представление о скорости изменения сигнала во времни.
В качестве такой «временной» характеристики широко используется автокор еляционная функция сигнала. Для детерменированного сигнала 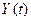 конечной длительности автокорреляционная функция имеет вид
конечной длительности автокорреляционная функция имеет вид
Функциональная схема ее реализации представлена на рис.
| |||
 | |||
|
|
 | ||||||||||
 |  | |||||||||
 | ||||||||||
 | ||||||||||
 |
Рис. Модель реализаций корреляционной функции
л.з.- линия задержки, &-умножит.
Корреляционная функция детерминированного сигнала с конечной энергией представляет собой интеграл от произведения двух копий сигнала, сдвинутых друг относительно друга за время т. е.корреляционная функция представляет собой интегральное преобразование сигнала.

Рис.5.2. Геометрическое построение автокорреляционной функции.
Модуль автокорреляционной функции будет зависеть только от  .
.
Корреляционная функция показывает степень сходства между сигналом и ее сдвинутой копией. Чем больше значение корреляционной функции, тем это сходство сильнее.
Корреляционная функция обладает следующими свойствами:
1. Значение корреляционной функции при  равно энергии сигнала, т.е. интегралу от квадрата этих функций.
равно энергии сигнала, т.е. интегралу от квадрата этих функций.
 (5.1)
(5.1)
2. Корреляционная функция является четной функцией своего аргумента, т. е.  .
.
3. Значение корреляционной функции при  является максимально возможным значением. С ростом абсолютного значения
является максимально возможным значением. С ростом абсолютного значения  , корреляционная функция с конечной энергией затухает.
, корреляционная функция с конечной энергией затухает.
4. Если сигнал – напряжение [В], то корреляционная функция имеет размерность [В2• сек].
В случае периодического сигнала или в случае любого сигнала с бесконечной энергией пользуются преобразованием за один период, т.е.
 (5.2)
(5.2)
В этом случае значения корреляционной функции при  равно не энергии, а средней мощности анализируемого сигнала. Свойство четности сохраняется. Значение корреляционной функции при
равно не энергии, а средней мощности анализируемого сигнала. Свойство четности сохраняется. Значение корреляционной функции при  является максимально возможным значением. Размерность корреляционной функции периодического сигнала равна квадрату размерности сигнала.
является максимально возможным значением. Размерность корреляционной функции периодического сигнала равна квадрату размерности сигнала.
Распределение вероятностей для суммы независимых случайных величин с произвольным законом распределения вероятностей, с ростом числа слагаемых стремится к нормальному закону распределения Гаусса

Нормальный закон распределения случайных величин чаще других встречается в природе. Он очень удобен для анализа, поэтому случайные процессы, распределение которых не слишком сильно отличается от нормальных, часто заменяют нормальными процессами. Особенно это актуально для описания помех каналов связи (канал, обеспечивающий прохождение сигнала).
Среди случайных сигналов можно выбрать стационарные, а из стационарных – эргодичные.
Эргодичный сигнал – сигнал, у которого мощность сигнала по одной реализации равна мощности сигнала по одной из составляющих за неограниченное время.
Подразумевая под случайным процессом ансамбль случайных функций, необходимо иметь в виду, что отдельным функциям, обладающим различной формой (закон изменения во времени) соответствуют различные спектральные характеристики. При этом среднее значение спектральной характеристики сигнала по всем реализациям будет равно нулю из-за случайности и независимости фаз спектральных составляющих во всех реализациях. Если использовать спектральную плотность среднего квадрата функции, то спектральная характеристика не равна нулю, т. к. она не зависят от фазировки суммируемых гармоник. Эту величину можно рассматривать как среднюю мощность, причем эта мощность распределена по частотам (гармоникам) в некоторой полосе, зависящей от механизма образования случайного процесса и от формы частотной характеристики измерительного преобразователя. Поэтому можно считать, что под спектральной плотностью средней мощности понимается мощность, приходящаяся на 1 Гц при заданной частоте 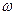 .
.
 - энергетический спектр функции
- энергетический спектр функции
Связь между корреляционной функцией и спектром:
Поскольку как корреляционная функция (  ), так и спектральная функция
), так и спектральная функция  являются интегральными преобразованиями анализируемого сигнала. Можно предположить, корреляционная функция спектральная связана между собой. Если к корреляционной функции применить преобразование Фурье, получим
являются интегральными преобразованиями анализируемого сигнала. Можно предположить, корреляционная функция спектральная связана между собой. Если к корреляционной функции применить преобразование Фурье, получим
 (5.3)
(5.3)
т.е. корреляционная функция связана преобразованием Фурье с квадратом модуля спектральной функции или, что то же самое, с энергетическим спектром сигнала.
Теорема Винера - Хинчена:
 – прямое преобразование Фурье (5.4)
– прямое преобразование Фурье (5.4)
 –обратное преобразование Фурье (5.5)
–обратное преобразование Фурье (5.5)
Корреляционная функция характеризует корреляцию функций, разделенных промежутком времени  . Чем медленнее изменяется во времени функция, тем больше промежуток
. Чем медленнее изменяется во времени функция, тем больше промежуток  , в пределах которого наблюдается статистическая связь между мгновенными значениями случайной функции. С другой стороны, изменение функции зависит от его спектра. Медленноменяющейся функции соответствует узкий спектр, а быстроменяющейся - широкий спектр. Из этого следует, что между автокорреляционной функцией и энергетическим спектром случайного процесса существует тесная связь.
, в пределах которого наблюдается статистическая связь между мгновенными значениями случайной функции. С другой стороны, изменение функции зависит от его спектра. Медленноменяющейся функции соответствует узкий спектр, а быстроменяющейся - широкий спектр. Из этого следует, что между автокорреляционной функцией и энергетическим спектром случайного процесса существует тесная связь.
Отсюда вытекает положение: чем шире энергетический спектр случайного процесса, тем меньше время корреляции и, соответственно, чем больше время корреляции, тем уже спектр процесса.
|
из
5.00
|
Обсуждение в статье: СПЕКТРАЛЬНЫЙ И КОРЕЛЛЯЦИОННЫЕ АНАЛИЗ СЛУЧАЙНОГО ПРОЦЕССА. ТЕОРЕМА ХИНЧЕНА–ВИННЕРА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

