 |
Главная |
Определение периодических несинусоидальных токов и напряжений
|
из
5.00
|
Периодическими несинусоидальными токами и напряженияминазывают токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону.
Они возникают при четырех различных режимах работы электрических цепей (и при сочетаниях этих режимов):
1) когда источник ЭДС (источник тока) дает несинусоидальную ЭДС (несинусоидальный ток), а все элементы цепи — резистивные, индуктивные и емкостные - линейны, т. е. от тока не зависят;
2) если источник ЭДС (источник тока) дает синусоидальную ЭДС (синусоидальный ток), но один или несколько элементов цепи нелинейны;
3) когда источник ЭДС (источник тока) дает несинусоидальнуюЭДС (несинусоидальный ток), а в состав электрической цепи входят один или несколько нелинейных элементов;
4) если источник ЭДС (тока) дает постоянную или синусоидальную ЭДС (ток), а один или несколько элементов цепи периодически изменяются во времени.
В данной главе рассматриваются методика расчета и особенности работы линейных электрических цепей при воздействии на них несинусоидальных ЭДС и токов - первый из перечисленных режимов работы.
Изображение несинусоидальных токов и напряжений с
помощью рядов Фурье.
Из курса математики известно, что любую периодическую функцию 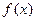 с периодом 2π, удовлетворяющую условиям Дирихле, можно разложить в тригонометрический ряд Фурье.
с периодом 2π, удовлетворяющую условиям Дирихле, можно разложить в тригонометрический ряд Фурье.
Функциональный ряд вида:
 (4.1)
(4.1)
называется тригонометрическим рядом, а постоянные  (n = 1, 2,…) называются коэффициентами тринонометрического ряда (4.1).
(n = 1, 2,…) называются коэффициентами тринонометрического ряда (4.1).
Частичные суммы  тригонометрического ряда (4.1) являются линейными комбинациями функций из системы функций
тригонометрического ряда (4.1) являются линейными комбинациями функций из системы функций  которая называется тригонометрической сиситемой. Так как членами этого ряда являются периодические функции с периодом 2π, то в случае сходимости ряда (1) его сумма
которая называется тригонометрической сиситемой. Так как членами этого ряда являются периодические функции с периодом 2π, то в случае сходимости ряда (1) его сумма  будет периодической функцией с периодом
будет периодической функцией с периодом  :
: 
 (-∞ +∞).
(-∞ +∞).
Определение.Разложить периодическую функцию 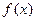 с периодом
с периодом 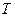 =2π в тригонометрический ряд (4.1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции
=2π в тригонометрический ряд (4.1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции 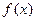 . Ортогональность тригонометрической системы
. Ортогональность тригонометрической системы
Определение.Функции 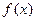 и
и  , непрерывные на отрезке [a, b], называются ортогональными на этом отрезке, если выполнено условие
, непрерывные на отрезке [a, b], называются ортогональными на этом отрезке, если выполнено условие  (4.2) Например, функции f(x) = x и g(x) =
(4.2) Например, функции f(x) = x и g(x) =  ортогональны на отрезке [-1, 1], так как
ортогональны на отрезке [-1, 1], так как

Нами было введено определение. Конечная или бесконечная система функций
 где
где 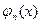 ≠ 0 (n = 1, 2,…), интегрируемых на отрезке [a, b], если для любых номеров m и n таких, что m ≠ n, выполняется равенство
≠ 0 (n = 1, 2,…), интегрируемых на отрезке [a, b], если для любых номеров m и n таких, что m ≠ n, выполняется равенство
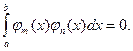
Теорема 1. Тригонометрическая система
1, cos x, sin x, cos 2x, sin 2x, …, cos nx, sin nx,…
ортогональна на отрезке [-π,π].
При любом целом n ≠ 0 имеем
 = 0,
= 0,  (4.3)
(4.3)
С помощью известных формул тригонометрии

 для любых натуральных m и n, m ≠ n, находим:
для любых натуральных m и n, m ≠ n, находим:
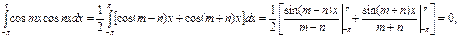
 Наконец, в силу формулы
Наконец, в силу формулы  для любых целых m и n получаем
для любых целых m и n получаем
 При m = n имеем
При m = n имеем


 (4.7)
(4.7)
Тригонометрический ряд Фурье
Поставим себе задачей вычислить коэффициенты  (n = 1, 2,…) тригонометрического ряда (1), зная функцию f(x).
(n = 1, 2,…) тригонометрического ряда (1), зная функцию f(x).
Теорема 2.Пусть равенство

имеет место для всех значений для всех значений х, причем ряд в правой части равенства сходится равномерно на отрезке [-  ]. Тогда справедливы формулы
]. Тогда справедливы формулы
 (n=0, 1, 2, …), (4.8)
(n=0, 1, 2, …), (4.8)
 (n=0, 1, 2, …) (4.9)
(n=0, 1, 2, …) (4.9)
Из равномерной сходимости ряда (1) вытекает непрерывность, а значит, и интегрируемость функции 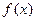 . Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать. Имеем
. Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать. Имеем
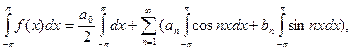 (4.10)
(4.10)
или

откуда и следует первая из формул (4.10) для n=0.
Умножим теперь обе части равенства (1) на функцию cos mx, где m – произвольное натуральное число:
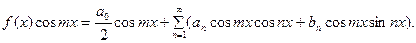 (3)
(3)
Ряд (3), как и ряд (1), сходится равномерно. Поэтому его можно интегрировать почленно,
 Все интегралы в правой части, кроме одного, который получается при n=m, равны нулю в силу ортогональности тригонометрической системы. Поэтому
Все интегралы в правой части, кроме одного, который получается при n=m, равны нулю в силу ортогональности тригонометрической системы. Поэтому
 (4.11)
(4.11)
откуда
 m=1, 2, … (4.12)
m=1, 2, … (4.12)
Аналогично, умножая обе части равенства (1) на sin mx и интегрируя от -  до
до  , получим
, получим

откуда
 m=1, 2, … (4.13)
m=1, 2, … (4.13)
Пусть дана произвольная периодическая функция 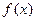 периода 2
периода 2  , интегрируемая на отрезке [-
, интегрируемая на отрезке [-  ]. Можно ли ее представить в виде суммы некоторого сходящегося тригонометрического ряда, заранее неизвестно. Однако по формулам (2) можно вычислить постоянные
]. Можно ли ее представить в виде суммы некоторого сходящегося тригонометрического ряда, заранее неизвестно. Однако по формулам (2) можно вычислить постоянные  и
и  .
.
Определение.Тригонометрический ряд

коэффициенты  которого определяются через функцию
которого определяются через функцию 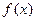 по формулам
по формулам
 n=0, 1, 2, …, (4.14)
n=0, 1, 2, …, (4.14)
 n=1, 2, …, (4.15)
n=1, 2, …, (4.15)
называется тригонометрическим рядом Фурье функции 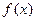 , а коэффициенты
, а коэффициенты  ,
,  , определяемые по этим формулам, называются коэффициентами Фурье функции
, определяемые по этим формулам, называются коэффициентами Фурье функции 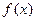 .
.
Каждой интегрируемой на отрезке [-  ] функции
] функции 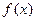 можно поставить в соответствие ее ряд Фурье
можно поставить в соответствие ее ряд Фурье

т.е. тригонометрический ряд, коэффициенты которого определяются по формулам (2). Однако если от функции f (x) не требовать ничего, кроме интегрируемости на отрезке  , то знак соответствия в последнем соотношении, вообще говоря, нельзя заменить знаком равенства.
, то знак соответствия в последнем соотношении, вообще говоря, нельзя заменить знаком равенства.
Замечание. Часто требуется разложить в тригонометрический ряд функцию f (x), определенную только на отрезке  и, следовательно, не являющуюся периодической. Так как в формулах (4.10) для коэффициентов Фурье интегралы вычисляются по отрезку
и, следовательно, не являющуюся периодической. Так как в формулах (4.10) для коэффициентов Фурье интегралы вычисляются по отрезку  , то для такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию f (x) периодически на всю ось Ox, то получим функция F(x), периодическую с периодом 2
, то для такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию f (x) периодически на всю ось Ox, то получим функция F(x), периодическую с периодом 2  , совпадающую с f (x) на интервале
, совпадающую с f (x) на интервале 
|
из
5.00
|
Обсуждение в статье: Определение периодических несинусоидальных токов и напряжений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

