Повторный отбор Бесповторный отбор

При определении

среднего размера

ошибки признака

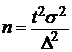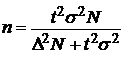(5); (6);

При определении

ошибки доли признака

 

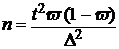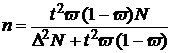(7); (8).

1) Известно, что N = 500; 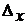= 0,5 млн. руб.; s² = 3,13; Р = 0,997; t = 3.

Найдем объем выборки для расчета ошибки средней:

при повторном отборе (по формуле 5) –

 

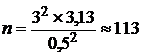заводов;

при бесповторном отборе (по формуле 6) –

 

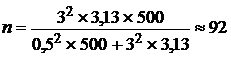завода.

2) Известно, что N = 500; 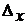= 0,5 млн. руб.; s² = 3,13; Р = 0,954; t = 2.

Определим объем выборки при бесповторном отборе (по формуле 6):

 

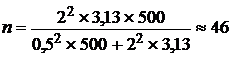завода.

3) Известно, что N = 500; 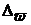= 0,5 млн. руб.; ω = 0,66; Р = 0,954; t = 2.

Объем выборки для расчета ошибки доли будет: при повторном отборе (по формуле 7) –

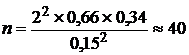заводов;

при бесповторном отборе (по формуле 8) –

 

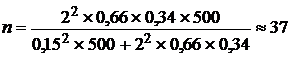заводов.

Выводы: 1) численность выборки увеличится, если при прочих равных условиях уменьшить предельную ошибку; 2) численность выборки уменьшится, если при прочих рав­ных условиях уменьшить вероятность, с которой требуется гарантировать результат выборочного обследования; 3) чис­ленность выборки уменьшится, если при прочих равных ус­ловиях увеличить предельную ошибку.

Пример 3. На заводе 1000 рабочих вырабатывают одноимен­ную продукцию. Из них со стажем работы до пяти лет тру­дятся 400 чел., а более пяти лет —600 чел. Для изучения среднегодовой выработки и установления доли квалифици­рованных рабочих проведена 10%-ная типическая выборка с отбором единиц пропорционально численности рабочих по указанным группам (внутри групп применялся случайный метод отбора).

На основе обследования получены следующие данные:

Группы рабочих со стажем работы	Об­щая чис­лен­ность рабочих, чел., N	Число обследо­ванных рабочих, чел., п	Средне­дневная выработ­ка, шт.,	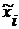Диспер­сия вы­работки, Число	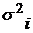Число квали­фициро­ванных рабочих в выработке, чел., m	Доля квали­фициро­ванных рабочих,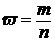
До 5 лет (включительно)						0,8
Свыше 5 лет						0,9
Итого

Определим: 1) с вероятностью 0,954 предельную ошибку выработки и границы, в которых будут находиться среднедневная выработка всех рабочих завода; 2) с той же вероятностью пределы удельного веса квалифицированных рабочих в общей численности рабочих завода.

Решение. 1) Средняя ошибка типической выборки определяется по формуле:

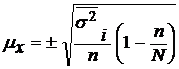(9)

где 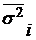– средняя из внутригрупповых дисперсий.

Она исчисляется по формуле:

;

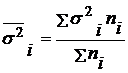Тогда

.

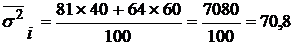Определим среднюю ошибку выборки при бесповторном отборе (по формуле 9) :

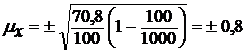шт.

Техника расчета предельной ошибки при типической вы­борке аналогична вышеизложенному расчету предельной ошибки при случайном отборе:

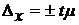или ;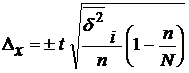

Подставив данные, получим: 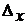= ± 2 × 0,83 = ± 1,6 шт.

Для определения возможных пределов среднедневной вы­работки всех рабочих завода первоначально нужно исчис­лить среднедневную выработку в выборочной совокупности по средней арифметической взвешенной:

 

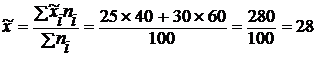шт.

Пределы среднедневной выработки всех рабочих завода: 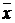= 28 ± 1,6 шт.

 

С вероятностью 0,954 можно утверждать, что среднеднев­ная выработка всех рабочих завода находится в пределах 26,4 шт. ≤ 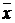≤ 29,6 шт.

2) Средняя ошибка репрезентативности для доли исчис­ляется по формуле:

 

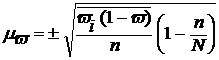(10)

где 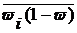– дисперсия доли ( 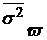) является средней из внутри групповых дисперсий.

Эта величина исчисляется по формуле:

 

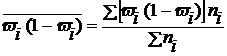
Технику расчета покажем в таблице:

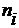
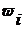
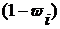
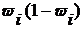
Группы рабочих со стажем работы	Чис­лен­ность рабо­чих,	Доля квали­фициро­ванных рабочих,	Доля малоквалифицированных рабочих,	Диспер­сия доли	Взвешен­ный пока­затель дис­персии,
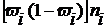
До 5 лет		0,8	0,2	0,16	6,4
Свыше 5 лет		0,9	0,1	0,09	5,4
Итого					11,8

 

Тогда

.

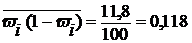Определим среднюю ошибку репрезентативности для доли (по формуле 10):

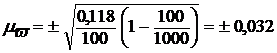, или ± 3,2%.

Исчислим среднюю ошибку выборочной доли с вероятностью 0,954:

 

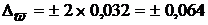, или 6,4%.

Расчет предела при установлении доли в общем виде представляется следующим образом:

.

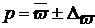Определим среднюю долю для выборочной совокупности:

 

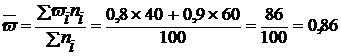, или 86%.

Отсюда: р = 86% ± 6,4%.

Вывод: с вероятностью 0,954 можно утверждать, что доля квалифицированных рабочих на заводе будет находить­ся в пределах 79,6% ≤ р ≤ 92,4%.

 

Пример 4. С целью определения среднего эксплуатационного пробега 10000 шин легковых автомобилей, распределенных, на партии по 100 шт., проводится серийная 4%-ная беспов­торная выборка. Результаты испытания отобранных шин ха­рактеризуются следующими данными:

Показатели	Партии
Средний эксплуатационный пробег шин, тыс. км
Доля шин с пробегом не ме­нее 42 тыс. км	0,80	0,85	0,90	0,95

 

Определите: 1) средние ошибки репрезентативности: а) эксплуатационного пробега шин; б) удельного веса шин с пробегом не менее 42 тыс. км; 2) с вероятностью 0,954 пределы, в которых будет находиться: а) средний эксплуа­тационный пробег всех обследуемых шин; б) доля шин, про­бег которых не менее 42 тыс. км в генеральной совокупности.

Решение. 1) При бесповторном отборе серий средняя ошибка репрезентативности определяется по формулам:

для средней –

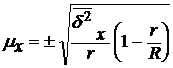(11)

для доли –

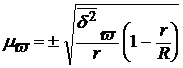(12)

где R – число серий в генеральной совокупности;

r – число отобранных серий;

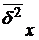– межсерийная дисперсия средних;

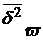– межсерийная дисперсия доли.

Сначала исчислим обобщающие показатели.

Средний эксплуатационный пробег шин:

 

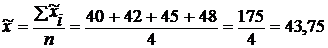тыс. км.

Средний удельный вес шин с пробегом не менее 42 тыс. км равен:

 

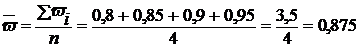(или 87,5%)

Межсерийная дисперсия определяется по формулам: для средней –

для средней –

;

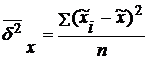для доли –

.

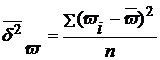Для ее расчета построим вспомогательную расчетную таб­лицу:

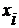
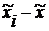
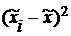
№ партии	Средний пробег шин, тыс. км.,			Доля шин с пробегом не менее 42 тыс. км.,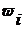
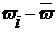
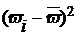
		-3,75	14,06	0,8	-0,075	0,005625
		-1,76	3,06	0,85	-0,025	0,000625
		1,25	1,56	0,90	0,025	0,000625
		4,25	18,06	0,95	0,075	0,005625
Итого			36,74			0,012500

 

Тогда

; .

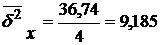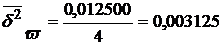Определим средние ошибки репрезентативности:

для средней (по формуле 11) –

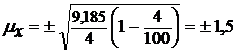тыс. км.;

для доли (по формуле 12) –

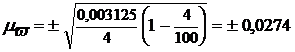, или ± 2,74%.

2) Определим с вероятностью 0,954 предельные ошибки репрезентативности для средней и для доли:

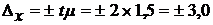тыс. км.;

%.

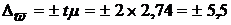Отсюда средний эксплуатационный пробег всех обсле­дуемых шин будет находиться в пределах:

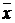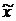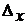= ± = 43,75 ± 3,0, или 40,75 тыс. км ≤ х ≤ 46,75 тыс. км.

Средний удельный вес шин с пробегом не менее 42 тыс. км в генеральной совокупности будет находиться в пределах:

p = 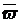± 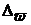= 87,5% ± 5,5%, или 82,0% ≤ р ≤ 93,0%.

 

Пример 5. Используя условие и решение предыдущей задачи, определите вероятность того, что: а) предельная ошибка выборки при установлении среднего эксплуатационного про­бега шин не превышает 4,0 тыс. км; б) доля шин с пробегом не менее 42 тыс. км будет находиться в пределах от 83% До 92%.

Решение. При определении вероятности используется формула предельной ошибки:

.

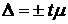В нашем примере следует использовать формулу пре­дельной ошибки серийного отбора.

а) Дано: R = 100; r = 4; 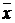= 43,75 тыс. км; 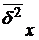= 9,185; 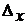= 4,0 тыс. км.

Требуется определить вероятность того, что разница сред­них величин эксплуатационного пробега шин в выборочной и генеральной совокупности не превысит ± 4,0 тыс. км, т. е.

р | 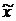– 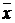| ≤ 4,0 тыс. км.

Подставляем данные в формулу:

;

 

;

 

.

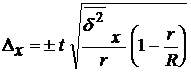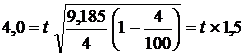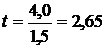По таблице значений вероятностей находим, что при t = 2,67 вероятность будет 0,992.

Следовательно, с вероятностью 0,992 можно гарантиро­вать, что средний эксплуатационный пробег шин легковых автомобилей в генеральной совокупности будет находиться в пределах 39,75 тыс. км ≤ 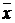≤ 47,75 тыс. км;

б) Дано: R = 100; r = 4; 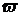= 87,5%; 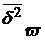= 0,003125; 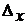= 4,5%.

Требуется определить: p | 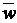– р | ≤ 4,5%, т. е. вероятность того, что доля шин с пробегом не менее 42 тыс. км в вы­борочной совокупности не будет отклоняться от доли гене­ральной совокупности более чем на 4,5%.

Подставив данные в формулу

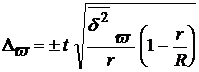
(см. решение выше), получим 4,5% = t × 2,74%;

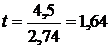, тогда Р = 0,899.

Следовательно, вероятность того, что удельный вес шин с пробегом не менее 42 тыс. км будет находиться в преде­лах от 83% до 92%, равна 0,899.