Тема 4. ПОКАЗАТЕЛИ ВАРИАЦИИ

ЗАДАЧИ

№ 1. По данным задачи № 1 темы «Средние величины» определите по какой бригаде: а) размах вариации; б) средний квадрат отклонения; в) среднее квадратическое отклонение; г) коэффициент вариации.

Сравните полученные показатели и сделайте выводы.

 

№ 2. Имеются следующие данные о работниках организации сферы обслуживания населения:

 

Рабочие, № п/п	Месячная заработная плата, руб.	Стаж работы, лет	Рабочие, № п/п	Месячная заработная плата, руб.	Стаж работы, лет

 

Определите по каждому признаку коэффициенты вариации. Сравните исчисленные показатели и сделай­те выводы.

 

№ 3. В лаборатории хлебозавода проведена контрольная проверка пористости хлеба. В результате получены следую­щие данные:

Пористость хлеба, %	Число проб
I партия	II партия	III партия	IV партия	V партия
2,5
3,5
4,0
5,0
Итого

 

Определите по каждой партии показатели вариации пористости хлеба: дисперсию; среднее квадратическое от­клонение; коэффициент вариации. При расчете дисперсии ис­пользуйте формулу:

 

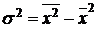
№ 5. По данным условия задачи № 7 темы «Средние величины» определите по каждому району показатели вариации распределения вкладов населения в сберегатель­ных кассах: дисперсию; среднее квадратическое отклонение; коэффициент вариации. При расчете дисперсии используйте способ моментов.

№ 6. Имеются следующие данные по двум группам ра­бочих:

Группы рабочих	Число рабо­чих, чел.	Средняя часо­вая выработка, шт.	Дисперсия выработки
Квалифицированные		5,5	0,23
Малоквалифицированные		3,5	0,38
Итого

 

Используя метод дисперсионного анализа, определи­те тесноту связи между квалификацией и средней выработ­кой рабочих, исчислив: а) коэффициент детерминации; б) эм­пирическое корреляционное отношение. Поясните полу­ченные результаты.

№ 7. По данным условия задачи № 7 темы «Средние ве­личины» исчислите по каждому району коэффициент асим­метрии распределения вкладов населения в сберегатель­ные кассы. Постройте график распределения.

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

Пример 1. Имеются следующие данные о распределении рабо­чих по тарифным разрядам:

Тарифный разряд
Число рабочих

 

Определите: а) дисперсию; б) среднее квадратическое отклонение; в) коэффициент вариации.

Решение. Дисперсия s², или средний квадрат для рядов распределения, исчисляется по формуле:

,

 

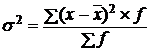т. е. является средней арифметической квадратов отклонений каждого значения признака от общей средней.

Корень квадратный из дисперсии называется средним квадратическим отклоноением:

.

 

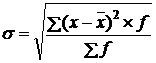Выражается он в единицах измерения изучаемого признака.

Коэффициент вариации – относительный показатель колеблемости, равный процентному отношению среднего квадратического отклонения к средней арифметической:

.

 

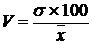Как величина относительная, выраженная в процентах, коэффициент вариации применяется для сравнения степени вариации различных признаков.

Как видно из формул, для расчета показателей вариации необходимо предварительно определить среднюю величину. Исчислим указанные выше показатели вариации, представив необходимые расчеты в таблице:

 

Тариф­ный раз­ряд, х	Число ра­бочих, чел., f	x f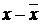
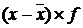
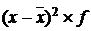
			- 2,5	- 2,5	6,25
			- 1,5	- 3,0	4,5
			- 0,5	3,0	1,5
			0,5	4,0	2,0
			1,5	4,5	6,75
Итого			-	-	21,0

 

Определим показатели:

.

 

.

 

.

 

.

 

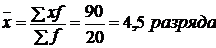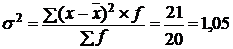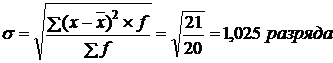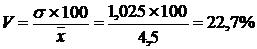Пример 2. По данным условия предыдущей задачи исчислим дисперсию по формуле:

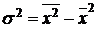
Решение. Все расчеты представим в таблице:

 

Тариф­ный раз­ряд, х	Число ра­бочих, чел., f	x f	х2	х2 f
Итого

 

Дисперсия равна:

 

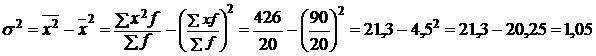
Среднее квадратическое отклонение:

 

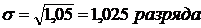
Пример 3. Имеются следующие данные о распределении ра­ботников организации сферы обслуживания населения по размеру средней месячной заработной платы:

Группы работников по размеру заработной платы, у.е.	Численность работников, чел.
До 100
100 – 120
120 – 140
140 – 160
160 – 180
180 – 200
Свыше 200
Итого

 

Определим дисперсию заработной платы по способу мо­ментов.

 

Решение. Способ моментов основан на математических свойствах дисперсии, применение которых значительно упро­щает технику ее вычисления, а для рядов распределения с равными интервалами приводит к формуле:

 

,

 

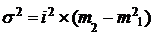где ; .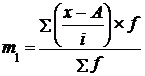

 

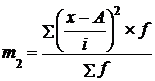Определим дисперсию по этой формуле, представив не­обходимые расчеты в таблице:

Группы работников по размеру заработной платы, у.е., x	Численность работников, чел., f	Середина интервала, x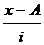
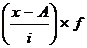
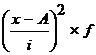
До 100			- 3	- 6
100 – 120			- 2	- 24
120 – 140			- 1	- 15
140 – 160
160 – 180
180 – 200
Свыше 200
Итого		-	-

 

Исчислим моме6нты первого и второго порядков (т₁ и т₂):

 

;

 

;

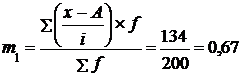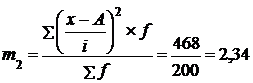i = 20 (величина интервала).

Затем вычислим средний квадрат отклонений (диспер­сию):

 

 

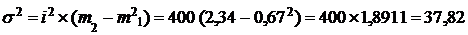
Пример 4. При обследовании произведенных 1000 единиц изделий 800 имели сертификат качества. Определите дисперсию и среднее квадратическое отклонение доли продукции с сертификатом качества.

Решение. Дисперсия альтернативного признака (или дисперсия доли) исчисляется по формуле:

,

 

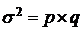где p – доля единиц, обладающих изучаемым признаком;

q – доля единиц, не обладающих этим признаком.

Следовательно, p + q = 1; q = 1 – p.

В нашем примере доля единиц, обладающих изучаемым признаком, т. е. доля продукции с сертификатом качества, равна: p = 800 : 1000 = 0,80, или 80%. Следовательно, 20% единиц не имели сертификат качества, т. е. не обладали изучаемым признаком. Эту величину можно получить двояко:

а) ;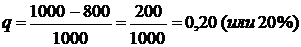

б) .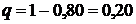

Следовательно, дисперсия доли продукции с сертификатом качества:

.

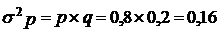Среднее квадратическое отклонение:

 

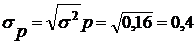
Пример 5. Для изучения взаимосвязи между стажем работы и производительностью труда (часовой выработкой) произве­дена следующая группировка рабочих:

 

Группа, №	Группы рабо­чих по стажу, лет	Число рабочих, чел.	Среднечасовая выработ­ка продукции одного рабочего, шт.
I	До 3		2; 2; 3; 3; 4
II	3 - 5		2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 4; 4;

 

Определите:

1) среднюю часовую выработку продукции по каждой группе рабочих и по двум группам вместе;

2) дисперсию по каждой группе рабочих (групповые дисперсии) и среднюю из групповых дисперсий;

3) дисперсию групповых средних от общей средней (меж­ групповую дисперсию);

4) общую дисперсию по правилу сложения дисперсий;

5) коэффициент детерминации;

6) эмпирическое корреляционное отношение.

Решение. 1. Определим среднюю выработку по каждой группе рабочих и по двум группам.

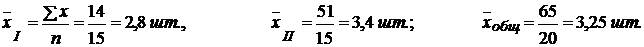
2. Исчислим дисперсии по каждой группе рабочих по формуле:

 

 

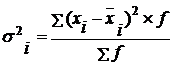
Предварительно строим по каждой группе рабочих ряды распределения по выработке. Затем исчислим групповые дисперсии.

 

 

Первая группа

Выработка, шт., х	Число рабочих, чел., f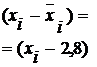
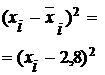
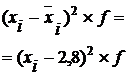
		- 0,8	0,64	1,28
		0,2	0,04	0,08
		1,2	1,44	1,44
Итого				2,80

 

Дисперсия для первой группы:

.

 

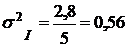Вторая группа

Выработка, шт., х	Число рабочих, чел., f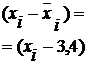
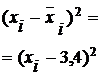
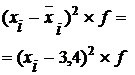
		- 1,4	1,96	3,92
		- 0,4	0,16	0,80
		0,6	0,36	2,88
Итого				7,60

 

Дисперсия для второй группы:

.

 

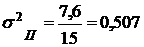Исчисли» среднюю из грушах (частных) дисперсий по формуле:

 

.

.

 

 

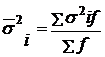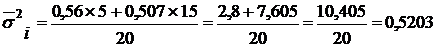3. Межгрупповая дисперсия:

;

 

.

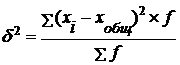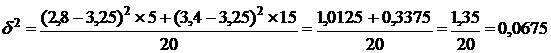4. Определим общую дисперсию по правилу сложения дисперсий:

 

;

 

.

 

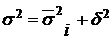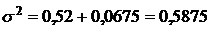5. Определяем коэффициент детерминации:

 

.

 

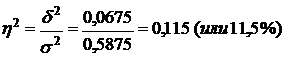Коэффициент детерминации показывает, что вариация среднечасовой выработки рабочих обусловлена вариацией стажа лишь на 11,5%.

6. Исчислим эмпирическое корреляционное отношение:

 

.

 

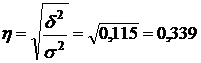Оно показывает, что для данной группы рабочих связь между производственным стажем и среднечасовой выработ­кой незначительная.

Пример 6. По данным условия задачи № 3 требуется опреде­лить коэффициент асимметрии по формуле:

.

 

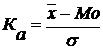Дисперсия известна по результатам задачи № 3: s² = 37,82. Следовательно, s = 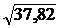= 6,15 руб.

Используя данные задачи № 3, исчислим:

а) среднюю заработную плату работников по способу мо­ментов:

 

 

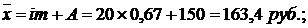
б) моду:

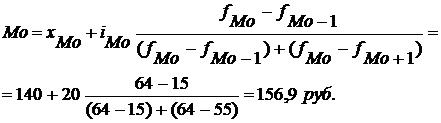
Отсюда коэффициент асимметрии равен:

.

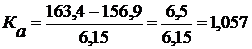Вывод: в данном ряду распределения имеется право­сторонняя асимметрия.

 

 

Тема 5. РЯДЫ ДИНАМИКИ

ЗАДАЧИ

№ 1. Имеются данные о розничном товарообороте района (млн. руб.):

Товарооборот района						200х
В старых границах				-	-	-
В новых границах	-	-

 

Приведите ряды динамики к сопоставимому виду (сомкните ряды). Укажите вид полученного ряда динамики. Начертите линейный график.

 

№ 2. Имеются следующие данные о производстве продукции предприятия за первое полугодие 2005 г. (млн. руб.):

Январь	Февраль	Март	Апрель	Май	Июнь

 

Исчислите среднемесячное производство продукции предприятия за первый квартал, за второй квартал и за полугодие в целом.

 

№ 3. Численность рабочих предприятия в течение 2004 г. характеризовалась следующими данными (чел.):

 

На 1/I На 1/III На 1/VII На 1/VIII На 1/I-2005 г.

520 510 530 505 524

Исчислите среднегодовую численность рабочих предприятия за 2004 г.

№ 4. Имеются следующие данные об остатках вкладов в сберегательном банке в первом полугодии 2005 г. (млн. руб.):

 

На 1/I	На 1/II	На 1/III	На 1/IV	На 1/V	На 1/VI	На 1/VII

 

Исчислите средние остатки вкладов в сберегательном банке: а) за первый квартал; б) за второй квартал; г) за полугодие в целом.

№ 5. Имеются следующие данные о производстве продукции промышленного предприятия за 2000 – 2005 гг. (в сопоставимых ценах; млн. руб.):

18,0	19,0	20,5	21,5	23,0	25,0

 

Для анализа динамики производства продукции предприятия исчислите:

1) среднегодовое производство продукции за двенадцатую пятилетку;

2) ежегодные и базисные абсолютные приросты, темпы роста и темпы прироста;

3) абсолютное значение одного процента прироста;

4) среднегодовой абсолютный прирост;

5) среднегодовой темп роста и среднегодовой темп прироста;

6) среднее значение одного процента прироста.

 

№ 6. Имеются следующие данные о ежесуточной выплавке чугуна по области в первой половине октября (тыс. т):

Дни	Выплавка	Дни	Выплавка	Дни	Выплавка
	30,3		35,3		36,5
	31,5		35,4		36,9
	33,0		35,1		39,3
	31,8		37,0		37,8
	32,1		34,5		36,9

 

Произведите сглаживание методом пятидневной скользящей средней.

 

№ 7. Реализация картофеля на колхозных рынка города за три года составила (тыс. т):

Месяцы	Годы
I	II	III
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь

 

Измерить сезонные колебания реализации картофеля, исчислив индексы сезонности методом отношений средних месячных к постоянной средней.

Постройте график сезонной волны продажи картофеля.

Объясните, для чего измеряют сезонные колебания.

 

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

 

Пример 1. В 2001 г. были изменены границы района. Данные о поголовье крупного рогатого скота в районе за 1999 – 2005 гг. приведены ниже (тыс. голов):

Поголовье скота
До изменения границ	45,0	48,0	50,0	-	-	-	-
После изменения границ	-	-	70,0	71,3	73,2	74,1	75,0

 

Требуется привести ряды динамики к сопоставимому виду.

Решение. Предварительно определим коэффициент пере­счета уровней в 2001г., в котором произошло изменение гра­ниц района: К = 70 : 50 = 1,4.

Умножая на этот коэффициент уровни ряда динамики в старых границах, получаем их сопоставимыми с уровнями в новых границах.

В 1999 г. …………………………………………………. 45 × 1,4 = 63,0 (тыс. голов).

В 2000 г. …………………………………………………. 48 × 1,4 = 67,2 (тыс. голов).

 

Теперь представим полученные данные о поголовье крупного рогатого скота в виде ряда динамики:

63,0	67,2	70,0	71,3	73,2	74,1	75,0

 

Полученные сопоставимые данные характеризуют рост поголовья крупного рогатого скота в районе за 1999 – 2005 гг. они могут быть использованы для расчета аналитических показателей ряда динамики.

 

Пример 2. Имеются следующие данные о производстве про­дукции предприятием за 2002 – 200х гг.. (тыс. руб.):

				200х

Требуется исчислить среднегодовое производство про­дукции за двенадцатую пятилетку.

Решение. Для интервального ряда динамики средний уро­вень исчислим по формуле средней арифметической простой:

 

 

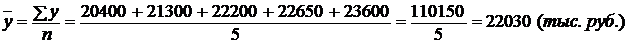
Пример 3. Имеются следующие данные об остатках сырья и материалов на складе предприятия (тыс. руб.):

 

На 1/I ………………………………………….400

На 1/II ………………………………………....455

На 1/III ………………………………………...465

На 1/IV …………………………………………460

 

Требуется определить среднемесячный остаток сырья и материалов на складе предприятия за I квартал.

Решение. По условию задачи имеем моментный ряд ди­намики с равными интервалами, поэтому средний уровень ряда будет исчислен по формуле средней хронологической:

 

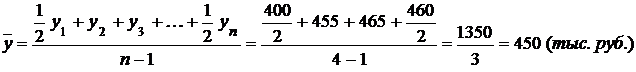
Пример 4. Имеются следующие данные о товарных запасах розничного торгового предприятия (млн. руб.):

На 1/I – 2004 г.	На 1/V – 2004 г.	На 1/VIII – 2004 г.	На 1/I – 2005 г.
61,1	57,5	51,3	74,7

 

Требуется исчислить среднегодовой товарный запас розничного торгового предприятия за 2004 г.

Решение. Имеем моментный ряд динамики с неравными интервалами. Средний уровень товарных запасов за год ис­числим по формуле:

 

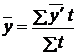
где 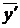– средние уровни в интервале между датами;

t – величина интервала времени (число месяцев между моментами времени).

Так, средний уровень товарных запасов равен:

 

с 1/I по 1/V ………………………………………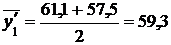

с 1/V по 1/VIII …………………………………... 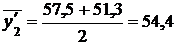и т.д.

 

Число месяцев (t) между моментами времени равно 4, 3, 5. Следовательно, средний уровень товарных запасов за год составит:

 

 

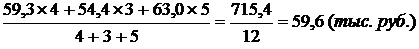
Пример 5. Автотранспортное предприятие по состоянию на 1 января 2005 г. имело 200 автомашин, 1 марта выбыло 5 автомашин, 1 сентября в распоряжение автотранспортного предприятия поступило 15 автомашин.

Требуется вычислить среднегодовую численность ав­томашин предприятия.

Решение. Представим вышеприведенные данные в виде моментного ряда динамики. Численность автомашин соста­вила (шт.) :

 

На 1/I …………………………………………...200

На 1/III ………………………………………....195

На 1/IX …………………………………………210

 

Представленный моментный ряд динамики имеет нерав­ные интервалы (2, 6, 4 месяца). Для такого типа задач средний уровень будет исчислен по формуле средней ариф­метической взвешенной:

 

 

 

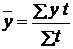
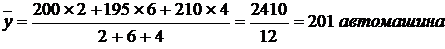
Пример 6. Имеются следующие данные о продукции промышленного предприятия за 2001 – 200х гг. (в сопоставимых ценах, млн. руб.):

					200х
8,0	8,4	8,9	9,5	10,1	10,8

 

Требуется исчислить аналитические показатели ря­да динамики производства продукции предприятия за годы двенадцатой пятилетки: абсолютные приросты, темпы роста, темпы прироста, абсолютное значение одного процента прироста, а также средние обобщающие показатели ряда динамики.

Решение. В зависимости от задачи исследования абсо­лютные приросты (∆у), темпы роста (Т) и темпы прироста (Т∆) могут быть исчислены с переменной базой сравнения (цепные) и с постоянной базой сравнения (базисные).

1. Абсолютный прирост (∆у) – это разность между пос­ледующим уровнем ряда и предыдущим (или базисным). Так, в 2002 г. прирост продукции равен: 8,4 – 8,0 = 0,4 млн. руб. Аналогично исчисляются абсолютные приросты за лю­бой год. В общем виде абсолютный прирост равен:

цепной базисный

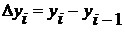
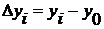
Результаты расчета показателей в табл. 1, гр. 2, 3.

Средний абсолютный прирост исчисляется двумя способами:

а) как средняя арифметическая простая годовых (цепных) приростов

 

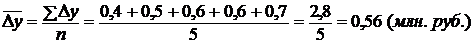
б) как отношение базисного прироста к числу периодов

 

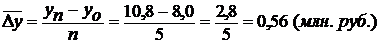
2. Темп роста (Т) – относительный показатель, харак­теризующий интенсивность развития явления. Он равен от­ношению изучаемых уровней и выражается в коэффициентах и процентах. Цепной темп роста исчисляют отношением последующего уровня к предыдущему: 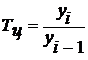, базисный – отношением каждого последующего уровня к одному уровню, принятому за базу сравнения: .

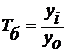Цепные темпы роста составили:

в 2002 г. по сравнению с 2001 г.

;

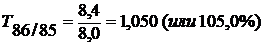в 2003 г. по сравнению с 2002 г.

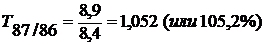и т.д.

Базисные темпы за эти же периоды равны:

;

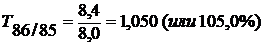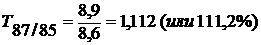т.д. (см. табл. 1, гр. 4, 5).

Между цепными и базисными темпами роста имеется взаимосвязь: произведение соответствующих цепных темпов роста равно базисному. Зная базисные темпы, можно ис­числить цепные делением каждого последующего базисного темпа роста на каждый предыдущий.

3. Темп прироста (ТА) определяют двумя способами:

а) как отношение абсолютного прироста к предыдущему уровню ( 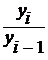– цепные) или базисному уровню ( 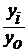– базисные):

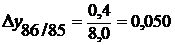(или 5,0%),

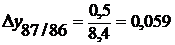(или 5,9%) и т.д.

(цепные – см. табл.1, гр. 6);

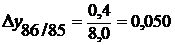(или 5,0%),

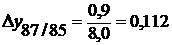(или 11,2%) и т.д.

(базисные – см. табл. 1, гр. 7);

б) как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах: Т∆=Т – 1; или как разность между темпами роста и 100%, если темпы ро­ста выражены в процентах: Т∆ = Т – 100%.

Следовательно, темп прироста в 2002 г. по сравнению с 2001 г. равен: 1,050 – 1 = 0,050, или 105% - 100% = 5,0% и т.д.

4. Абсолютное значение одного процента прироста равно отношению абсолютного прироста (цепного) к темпу прироста (цепному) (%):

 

.

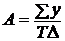Тогда

в 2002 г.

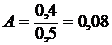(млн. руб.);

в 2003 г.

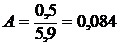(млн. руб.) и т.д.

Для наглядности единицы измерения удобнее записать в тыс. руб., т.е. 0,08 млн. руб. = 80 тыс. руб. и т.д.

Этот показатель может быть исчислен иначе: как одна сотая часть предыдущего уровня. Например, в 2003 г. по сравнению с 2002 г. абсолютное содержание, 1 % прироста составило: 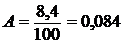(млн. руб.) = 84 (тыс. руб.) и т. д.

Расчет среднего абсолютного значения одного процента прироста за несколько лет производится по формуле:

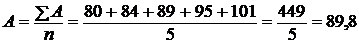(тыс. руб.)

Исчисленные выше аналитические показатели ряда ди­намики представим в таблице 1.

Таблица 1.