 |
Главная |
Реализация картофеля на колхозных рынках города за три года
|
из
5.00
|
| Месяцы | Реализация картофеля, т | Индексы сезонности, %
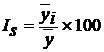
| ||||
Первый год, 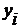
| Второй год, 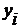
| Третий год, 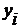
| Всего за три года, 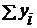
| В среднем за три года, 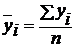
| ||
| А | ||||||
| Январь | 26,3 | |||||
| Февраль | 27,6 | |||||
| Март | 28,7 | |||||
| Апрель | 96,9 | |||||
| Май | 129,1 | |||||
| Июнь | 178,5 | |||||
| Июль | 110,0 | |||||
| Август | 41,0 | |||||
| Сентябрь | 243,3 | |||||
| Октябрь | 201,0 | |||||
| Ноябрь | 69,7 | |||||
| Декабрь | 47,9 | |||||
| Итого | 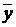 = 261 = 261
| 100,0 |
По индексам сезонности можно наблюдать рост или снижение продажи картофеля в различное время года. Так, наименьший спрос приходится на январь – февраль, а наибольший – на сентябрь – октябрь. Для наглядности можно построить график сезонной волны реализации картофеля.
Пример 10. Имеются следующие данные о внутригодовой динамике заголовок сельскохозяйственной продукции области по кварталам за три года:
| Месяцы | Заготовлено продукции, тыс. руб. | ||
| Первый год | Второй год | Третий год | |
| I | |||
| II | |||
| III | |||
| IV |
Для анализа внутригодовой динамики заготовок сельскохозяйственной продукции области требуется исчислить индексы сезонности.
Решение. Вычисление индексов сезонности в рядах динамики с тенденцией развития (к переменной средней).По аналогии с предыдущим примером для каждого года квартальные уровни укрупним до годовых и по ним исчислим темпы роста:
| Годы | Годовые уровни, тыс. руб. | Темпы роста, % | |
| к предыдущем году | к первому году | ||
| Первый год | - | ||
| Второй год | 105,8 | 105,8 | |
| Третий год | 106,3 | 112,4 |
Можно заметить, что ряд динамики имеет четкую тенденцию роста заготовок, это подтверждают довольно высокие цепные и базисные темпы роста.
Для анализа рядов внутригодовой динамики, в которых наблюдается тенденция роста, изучение сезонности основано на методе переменной средней.
Для расчета индекса сезонности в таких рядах динамики применяется формула:
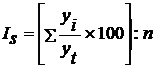
где 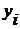 – фактические (эмпирические) уровни ряда;
– фактические (эмпирические) уровни ряда;
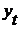 – выравненные (теоретические) уровни ряда;
– выравненные (теоретические) уровни ряда;
п – число лет.
Определим теоретические значения ( 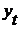 ) по уравнению:
) по уравнению:
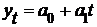 .
.
Для расчета параметров 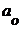 и
и 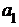 составим таблицу 6.
составим таблицу 6.
Таблица 6
Расчет параметров 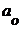 и
и 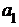
| Период | Эмпирические уровни ряда, 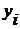
| Обозначения времени, t | t2 | yt | 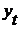
| 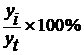
|
| А | ||||||
| Первый год | ||||||
| I квартал | - 5,5 | 30,25 | - 891,0 | 162,6 | 99,6 | |
| II » | - 4,5 | 20,25 | - 765,0 | 164,8 | 103,2 | |
| III » | - 3,5 | 12,25 | - 619,5 | 167,1 | 195,9 | |
| IV » | - 2,5 | 6,25 | - 377,5 | 169,4 | 89,1 | |
| Второй год | ||||||
| I квартал | - 1,5 | 2,25 | - 238,5 | 171,6 | 92,7 | |
| II » | - 0,5 | 0,25 | - 96,5 | 173,9 | 111,0 | |
| III » | 0,5 | 0,25 | 89,0 | 176,1 | 101,1 | |
| IV » | 1,5 | 2,25 | 252,0 | 178,4 | 94,2 | |
| Третий год | ||||||
| I квартал | 2,5 | 6,25 | 395,0 | 180,7 | 87,4 | |
| II » | 3,5 | 12,25 | 787,5 | 182,9 | 123,0 | |
| III » | 4,5 | 20,25 | 841,5 | 185,2 | 101,0 | |
| IV » | 5,5 | 30,25 | 946,0 | 187,3 | 91,8 | |
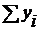 = 2100 = 2100
| å t = 0 | å t2 = 143,00 | å yt = 323 | å yt = 2100 |
Исчислим параметры:
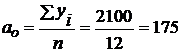 ;
;
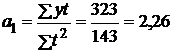
ледовательно,стема нормативных управлений примет вид:
ваемого периода:
.
Следовательно, уравнение прямой примет вид:
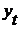 = 175 + 2,26 t.
= 175 + 2,26 t.
Подставив в полученное уравнение значения t (квартальные), получим выравненные значения ряда:
Для первого года
I квартал....... . 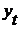 = 175 + 2,26 х (- 5,5) = 175 – 12,43 = 162,6;
= 175 + 2,26 х (- 5,5) = 175 – 12,43 = 162,6;
II квартал...... . 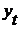 = 175 + 2,26 х (- 4,5) = 175 – 10,17 = 164,8;
= 175 + 2,26 х (- 4,5) = 175 – 10,17 = 164,8;
III квартал...... 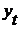 = 175 + 2,26 х (- 3,5) = 175 – 7,91 = 167,1
= 175 + 2,26 х (- 3,5) = 175 – 7,91 = 167,1
и т. д. (см. табл. 6, гр. 5).
Далее необходимо найти для каждого квартала процентные отношения эмпирических уровней ряда ( 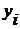 ) к теоретическим уровням (
) к теоретическим уровням ( 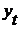 ), т. е.
), т. е. 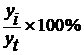 .
.
Тогда, для первого года
I квартал ………...… 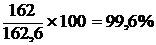 .
.
II квартал …… 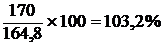 и т.д.
и т.д.
Для третьего года
IV квартал ……….… 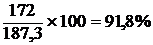 .
.
После этого нужно просуммировать полученные процентные отношения ( 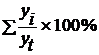 ) за три года по одноименным кварталам (см. табл. 7):
) за три года по одноименным кварталам (см. табл. 7):
I квартал…….99,6 + 92,7 + 87,4 = 279,7;
II квартал……103,2 +111,0 +123,0 = 337,2 и т.д.
Затем следует исчислить индексы сезонности (см. табл. 7, гр. 11).
| Квар талы | Фактические
данные, 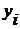
| Выравненные данные, 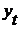
| Фактические данные в процентах к выравненным, 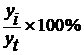
| Сумма процентных отношений (гр. 7 + гр. 8 + гр.9) | Индексы
сезонности, %,
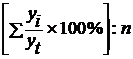
| ||||||
| Пер вый год | Вто рой год | Тре тий год | Пер вый год | Вто рой год | Тре тий год | Пер вый год | Вто рой год | Тре тий год | |||
| А | |||||||||||
| I | 162,6 | 171,6 | 180,8 | 99,6 | 92,7 | 87,4 | 279,7 | 93,2 | |||
| II | 164,8 | 173,9 | 182,9 | 103,2 | 111,0 | 123,0 | 337,2 | 112,4 | |||
| III | 167,1 | 176,1 | 185,2 | 105,9 | 101,1 | 101,0 | 308,0 | 102,7 | |||
| IV | 169,4 | 178,4 | 187,3 | 89,1 | 94,2 | 91,8 | 275,1 | 91,7 | |||
| Итого | - | - | - | - | - | - | - | 100,0 |
Индексы сезонности характеризуют размеры заготовок сельскохозяйственной продукции в зависимости от времени года. Наибольший удельный вес заготовок сельскохозяйственной продукции приходится на второй квартал. Чтобы наглядно представить сезонную волну, индексы сезонности наносят на график.
Тема 6. ИНДЕКСЫ
ЗАДАЧИ
№ 1. Имеются следующие данные о количестве произведенной продукции и ее себестоимости по предприятию:
| Продукция | Количество произведенной продукции, тыс. шт. | Себестоимость единицы продукции, руб. | ||
| 2003 г. | 2005 г. | 2003 г. | 2005 г. | |
| КС | 3,0 | 3,2 | 1,0 | 1,0 |
| МП | 4,0 | 5,0 | 2,0 | 1,8 |
| КМ | 5,0 | 6,0 | 0,8 | 0,6 |
Вычислить: 1) индивидуальные индексы себестоимости и количества произведенной продукции; 2) общие индексы: а) затрат на продукцию; б) физического объема продукции; в) себестоимости и экономический эффект от снижения себестоимости продукции.
Покажите взаимосвязь между исчисленными индексами.
№ 2. Имеются следующие данные о реализации товаров:
| Товар | Товарооборот в ценах соответствующего года, тыс. руб. | Изменение цен в 2005 г. к 2003 г., % | |
| 2003 г. | 2005 г. | ||
| Шерстяные ткани | - 10 | ||
| Одежда | + 5 | ||
| Обувь | + 8 |
Вычислить: 1) общий индекс товарооборота; 2) общий индекс цен; 3) общий индекс физического объема товарооборота.
№ 3. Имеются следующие данные о продаже товаров в магазинах города:
| Товарная группа | Продано в2004 г., тыс. руб. | Изменение количества проданных товаров в 2005 г. к 2004 г., % |
| Трикотажные изделия | + 12 | |
| Швейные изделия | + 20 | |
| Обувь | - 5 |
Вычислить: 1) общий индекс физического объема товарооборота в 2005 г. по сравнению с 2004 г.; 2) общий индекс цен, если известно, что товарооборот в фактических ценах за этот период вырос на 12%.
№ 4. Товарооборот республики в 2005 г. по сравнению с 2004 г. вырос на 6%, розничные цены в среднем повысились на 4%. Как изменился физический объем товарооборота?
№ 5. Как в среднем изменились цены, если известно, что товарооборот вырос на 18%, а физический объем товарооборота увеличился на 16%?
№ 6.имеются следующие данные о производстве однородной продукции по двум заводам:
| Завод | Выработано продукции «А», тыс. шт. | Затраты на продукцию, тыс. шт. | ||
| 2003 г. | 2005 г. | 2003 г. | 2005 г. | |
| № 1 | ||||
| № 2 |
Вычислить: 1) индекс себестоимости переменного состава; 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов.
Покажите взаимосвязь исчисленных индексов. Поясните полученные результаты.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Пример 1.Имеются данные о продаже товаров на колхозных рынках города в январе месяце:
| Товар | Продано товара, тыс. ед. | Средняя цена единицы товара, руб. | ||
| 2003 г. | 2005 г. | 2003 г. | 2005 г. | |
| Морковь, кг | 15,0 | 16,2 | 8,0 | 7,0 |
| Яблоки, кг | 50,0 | 51,0 | 25,0 | 35,0 |
Вычислить: 1) индивидуальные индексы цен и количества проданного товара; 2) общий индекс товарооборота; 3) общий индекс физического объема товарооборота; 4) общей индекс цен и сумму экономии или перерасхода от изменения цен; 5) прирост товарооборота за счет изменения цен и количества продаж товаров.
Покажите взаимосвязь между исчисленными индексами.
Решение. 1. Индивидуальные индексы (однотоварные) равны:
а) цен
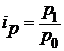 .
.
б) количества проданных товаров
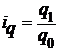 .
.
Так, для моркови 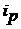 = 7,0 : 8,0 = 0,875 (87,5%). Следовательно, цена на морковь снизилась на 12,5%.
= 7,0 : 8,0 = 0,875 (87,5%). Следовательно, цена на морковь снизилась на 12,5%.
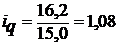 т. е. количество проданной моркови выросло на 8%. Соответствующие индексы для яблок будут равны
т. е. количество проданной моркови выросло на 8%. Соответствующие индексы для яблок будут равны 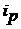 = 1,4 и
= 1,4 и 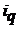 = 1,02.
= 1,02.
2. Общий индекс товарооборота исчисляется по формуле:
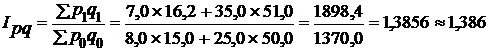 (138,6%).
(138,6%).
Товарооборот в январе 1988 г. вырос на 38,6% по сравнению с январем 2003г.
3. Общий индекс физического объема товарооборота (количества проданных товаров) исчисляется по следующей агрегатной форме индекса:
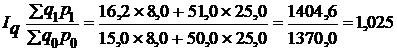 ,
,
или 102,5%. Это значит, что количество проданного товара в отчетном периоде было на 2,5% больше, чем в базисном периоде.
4. Общий индекс цен равен:
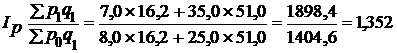 , (135,2%)
, (135,2%)
т. е. цены на оба товара в среднем выросли на 35,2%.
Экономический эффект или иначе сумма сэкономленных или перерасходованных денег за счет изменения цен исчисляется по данным общего индекса цен и равна разнести числителя и знаменателя индекса: 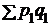 –
– 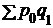 = 1898,4 – 1404,6 = 493,8 тыс. руб. Следовательно, в связи с ростом цен на 35,2%'население в отчетном периоде дополнительно израсходовало 493,8 тыс. руб. на покупку данного товара.
= 1898,4 – 1404,6 = 493,8 тыс. руб. Следовательно, в связи с ростом цен на 35,2%'население в отчетном периоде дополнительно израсходовало 493,8 тыс. руб. на покупку данного товара.
5. Прирост товарооборота исчисляется как разность между числителем и знаменателем индекса товарооборота: 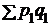 –
– 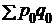 = 1898,4 – 1370,0 = 528,4 тыс. руб. Этот прирост обусловлен изменением цен на товары и изменением количества проданных товаров. Прирост за счет изменения цен составил: 1898,4 – 1404,6 = 493,8 тыс. руб. и за счет изменения количества проданных товаров: 1404,6 – 1370,0 = 34,6 тыс.руб. Следовательно, увеличение товарооборота на 528,4 тыс. произошло за счет роста цен на 493,8 тыс. руб. и роста количества проданного товара на 34,6 тыс. руб. (493,8 + 34,6 = 528,4 тыс. руб.).
= 1898,4 – 1370,0 = 528,4 тыс. руб. Этот прирост обусловлен изменением цен на товары и изменением количества проданных товаров. Прирост за счет изменения цен составил: 1898,4 – 1404,6 = 493,8 тыс. руб. и за счет изменения количества проданных товаров: 1404,6 – 1370,0 = 34,6 тыс.руб. Следовательно, увеличение товарооборота на 528,4 тыс. произошло за счет роста цен на 493,8 тыс. руб. и роста количества проданного товара на 34,6 тыс. руб. (493,8 + 34,6 = 528,4 тыс. руб.).
Между исчисленными индексами существует взаимосвязь:
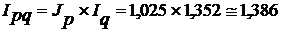 .
.
Пример 2. Имеются следующие данные о продаже товаров в универсаме города:
| Товарные группы | Продано в 2004 г., тыс. руб., 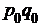
| Индексы количества проданных товаров в 2005 г. к 2004 г., %, 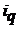
|
| Обувь | 0,98 | |
| Ткани | 1,05 | |
| Галантерея | 1,2 |
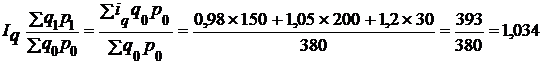 (103,4%).
(103,4%).
Пример 3. Имеются следующие данные о продаже товаров магазина потребительской кооперации за два квартала 2005 г.:
| Товары | Товарооборот в действующих ценах, тыс. руб. | Изменение средних цен во II квартале по сравнению с I кварталом, % | |
| I квартал | II квартал | ||
| Овощи | - 20 | ||
| Мясо и мясопродукты | + 10 | ||
| Зерно | без изменения |
Вычислить: 1) общий индекс товарооборота; 2) общий индекс цен; 3) сумму экономии (или перерасхода), полученную населением от изменения цен; 4) общий индекс физического объема товарооборота.
Решение. Общий индекс товарооборота равен:
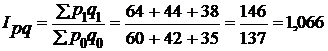 (106,6%)
(106,6%)
Товарооборот во II квартале вырос по сравнению с первым кварталом на 6,6%.
Общий индекс цен исчислим по формуле среднегарионического индекса, который тождествен агрегатной форме индекса:
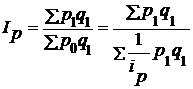 .
.
Для вычисления этого индекса определим предварительно индивидуальные индексы цен:
для овощей
100 – 20 = 80 %, или 0,80 в коэффициентах;
мяса и мясопродуктов
100 + 10 =110 %, или 1,10 в коэффициентах;
зерна
100%, или 1.
Следовательно,
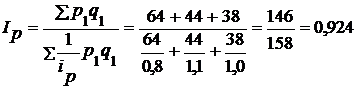
или 92,4 %, т.е. цены в среднем снизились на 7,6 %.
Сумма экономии, полученная населением от снижения цен, составила: 146 – 158 = -12 тыс. руб.
Общий индекс физического объема товарооборота (количества проданного товара) может быть исчислен с помощью взаимосвязи индексов:
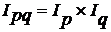
Следовательно, 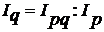 = 1,066 : 0,924 = 1,153 (115,3%),
= 1,066 : 0,924 = 1,153 (115,3%),
Пример 4. Имеются следующие данные о продаже товаров на колхозных рынках города в I квартале 2005 г.
| Товар | Продано, тыс. ед., q | Цена единицы товара, руб., р | ||||
| январь (1) | февраль (2) | март (3) | январь (1) | февраль (2) | март (3) | |
| соль «Экстра | ||||||
| соль иодированная | 2,5 | 3,0 | 3,3 |
Вычислить: 1) индивидуальные цепные и базисные индексы цен на соль иодированную; 2) общие цепные и базисные индексы цен и физического объема товарооборота.
Решение. 1. Цепные и базисные индексы цен:
а) цепные 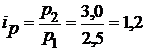 ;
; 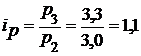 ;
;
б) базисные 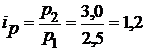 ;
; 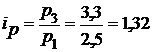 .
.
Между цепными и базисными индивидуальными индексами существует связь – произведение цепных индексов равно базисному:
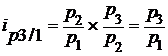
Зная базисные индексы, можно вычислить цепные, разделив последующий базисный индекс на предыдущий. Например,
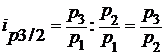
Аналогично исчисляются индивидуальные индексы количества проданных товаров.
2. Исчислим общие индексы цен:
а) цепные 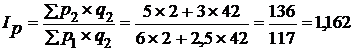 , или 116,2%,
, или 116,2%,
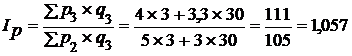 , или 105,7%.
, или 105,7%.
б) базисные 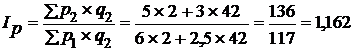 , или 116,2%,
, или 116,2%,
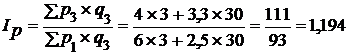 , или 119,4%.
, или 119,4%.
Как видно из вычислений, цепные общие индексы цен имеют переменные веса на уровне отчетного периода. Для таких индексов нет взаимосвязи между цепными и базисными индексами, что характерно для всех качественных индексов.
Исчислим общие индексы физического объема товарооборота:
а) цепные 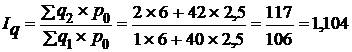 , или 110,4%,
, или 110,4%,
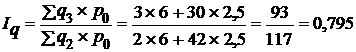 , или 79,5%,
, или 79,5%,
б) базисные 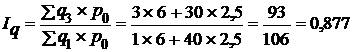 , или 87,7%,
, или 87,7%,
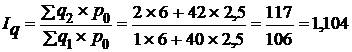 , или 110,4%,
, или 110,4%,
Данные примера показывают, что цепные и базисные индексы количественных показателей взвешиваются по постоянным весам, следовательно, между ними имеется связь:
произведение цепных индексов равно базисному:
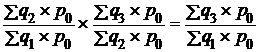 ,
,
или 1,104 × 0,795 = 0,877
От базисных индексов можно перейти к цепным, как это показано выше.
Пример 5. Имеются следующие данные о выпуске продукции «А» по двум заводам:
| № завода | Базисный период | Отчетный период | ||||
| произведено продукции, тыс. шт. | себестоимость единицы, руб. | удельный вес продукции, % | произведено продукции, тыс. шт. | себестоимость единицы, руб. | удельный вес продукции, % | |
| q0 | z0 | d0 | q1 | z1 | d1 | |
| - | - |
Вычислить: 1) индекс себестоимости переменного состава; 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов.
Решение. 1. вычислим индекс себестоимости переменного состава, который равен соотношению средней себестоимости продукции по двум заводам:
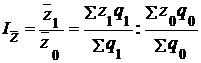 ;
;
Средняя себестоимость продукции по двум заводам в отчетном и базисном периодах равна:
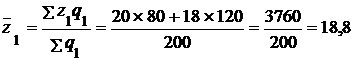 руб.
руб.
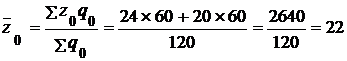 руб.
руб.
Следовательно, индекс себестоимости переменного состава равен:
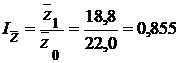 , или 85,5%.
, или 85,5%.
Индекс показывает, что средняя себестоимость изделия по двум заводам снизилась на 14,5%. Это снижение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры продукции (удельного веса продукции заводов). Выявим влияние каждого из этих факторов на динамику средней себестоимости, исчислив индексы себестоимости постоянного состава и структурных сдвигов.
2. Индекс себестоимости постоянного состава (индекс в постоянной структуре):
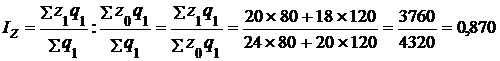 .
.
Себестоимость продукции по двум заводам в среднем снизилась на 13%.
3. Индекс структурных сдвигов равен:
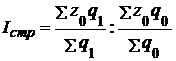 .
.
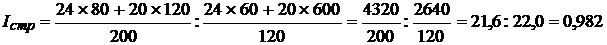 ,
,
или 98,2%.
Средняя себестоимость изделия в отчетном периоде снизилась дополнительно на 1,8% за счет увеличения доли продукции 2-го завода с 50 до 60%, на котором уровень себестоимости продукции был ниже по сравнению с первым заводом.
Исчисленные выше индексы можно вычислить по удельным весам продукции заводов, выраженных в коэффициентах:
а) индекс себестоимости переменного состава –
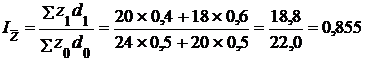 ;
;
б) индекс себестоимости постоянного состава –
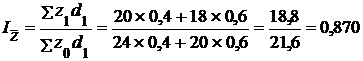 ;
;
в) индекс структурных сдвигов –
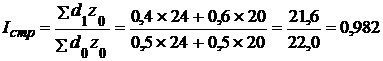 .
.
Индекс структурных сдвигов может быть вычислен также с помощью взаимосвязи индексов. Известно, что индекс переменного состава равен произведению индексов постоянного состава и структурных сдвигов:

Следовательно, 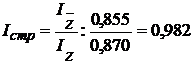 .
.
|
из
5.00
|
Обсуждение в статье: Реализация картофеля на колхозных рынках города за три года |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

