Различие безрисковых ставок кредитования и инвестирования

Рассмотрим теперь - как изменятся наши выводы, если мы ослабим некоторые из принятых нами предположений, приблизив тем самым нашу модели к реальности. Предположение о существовании единой безрисковой ставки как по кредитам, так и по инвестициям является, естественно, сильным упрощением. В реальности мы, как правило, наблюдаем, что ставки доходности, по которым мы можем инвестировать средства, отличаются от ставок кредитования. Причем, часто ставки доходности инвестиций для отдельного инвестора меньше ставок, по которым он может взять средства в долг. Обозначим m0с - безрисковая ставка по займам, m0i - безрисковая ставка доходности по инвестициям, причем m0с > m0i .

Эффективное множество при этом существенно изменится. Пусть, как и прежде EE’ - граница допустимого множества комбинаций риска и доходности для рискованных активов. В случае сочетания рискованных и безрисковых инвестиций, достижимые комбинации риска и доходности лежат на отрезке O1M1, где M1 - это точка касания луча опущенного из точки O1 (значение m_0i) к кривой EE’. Если же инвестор стремится к большему доходу, чем обеспечивает портфель М1 и, соответственно, готов идти на больший риск, его выбором может стать инвестирование исключительно в один из рискованных портфелей, риск и доходность которых лежит на участке M1M2 кривой EE’. Наконец, еще более агрессивный инвестор выберет решение, при котором инвестиции будут производится в портфель M2 за счет кредитования по ставке m0с. Возможные сочетания риска и дохода в последнем случае лежат на участке касательной, проведенной из точки O к кривой EE’, начиная с точки M2 (рисунок 6-9).

Таким образом, если ставки доходности безрисковых инвестиций и кредитов различаются, множество эффективности состоит из 3-х участков, и портфель рискованных активов не будет для всех одинаковым. В зависимости от степени несклонности к риску, инвесторы будут выбирать различные портфеиь рискованных активов, риск и доходность которых лежат на участке M₁M₂ кривой EE’.

Модель Марковица

Модель поведения инвестора, согласно которой инвестиции оцениваются исключительно по двум параметрам - ожидаемой доходности и риску, измеряемому как величина стандартного отклонения доходности, позволяет сформулировать единое правило формирования портфеля, которому следуют все без исключения инвесторы: независимо от индивидуальных предпочтений, все инвесторы стремятся сформировать эффективный портфель - такой, который обеспечивает минимальную степень риска для выбранного уровня дохода, либо, что то же самое, максимальный ожидаемый доход при заданной степени риска. Этот подход, и сама задача, выбора эффективного портфеля носит название модели Марковица.

Пусть, как и прежде, существует n активов, каждый из которых обеспечивает случайную величину доходности xi­ (i=1,...,n), mi - ожидаемая (средняя) доходность i-го актива (математическое ожидание случайной величины xi):

,

- стандартное отклонение доходности i-го актива:

,

- ковариация между доходностями i-го и j-го активов:

,

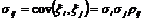(rij - коэффициент корреляции случайных величин xi и xj).

Модель Марковица можно сформулировать следующим образом: необходимо найти такие пропорции распределения средств между доступными активами: x1,x2,...,xn (где xi - доля средств, инвестируемых в i-й актив), чтобы риск портфеля при заданном уровне доходности был бы минимальным. Математически модель можно сформулировать так: найти

, (6.20)

при ограничениях

(6.21)

В приведенной формулировке модели, - заданный уровень средней доходности,

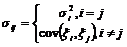
(согласно принятым обозначениям).

Модель можно записать в матричной форме, обозначив: x - вектор распределения средств между рискованными активами: x={xi}i=1,...,n; - вектор доходности активов, V - ковариационная матрица (квадратная матрица, состоящая из значений sij, i=1,...,n; j=1,...,n ). Тогда необходимо найти

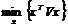, (6.22)

при ограничениях

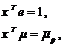(6.23)

где e - единичный вектор:

,

T - знак транспонирования вектора.

Для модели (6.22), (6.23) легко найти аналитическое решение

,

где и - множители Лагранжа ограничений (6.23).

Если существует безрисковый актив, модель можно записать

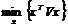, (6.24)

, (6.25)

, (6.26)

где m0 - безрисковая ставка, x0 - доля богатства, инвестируемая в безрисковый актив. От ограничения (6.26) можно избавиться, сделав замену:

. (6.27)

Тогда ограничение (6.25) будет выглядеть как

, (6.28)

и решение задачи (6.24)-(6.26) можно записать

,

где j - множитель Лагранжа ограничения (6.28).