Гомоморфизм и изоморфизм алгебр

Дипломная работа специалиста

студент 5 курса специальности математика _________________________________   НАУЧНЫЕ РУКОВОДИТЕЛИ: ассистент каф. алгебры и функционального анализа _________________________________   профессор, доктор физико-математических наук _________________________________   РЕШЕНИЕ О ДОПУСКЕ К ЗАЩИТЕ: зав. кафедрой, профессор, д.ф.м.н. _________________________________

 

 

СИМФЕРОПОЛЬ

2003

 

 

СОДЕРЖАНИЕ

 

Введение……………………………………………………………………………..4

Глава I . Основные понятия и определения…………………………………….6

§ 1. * - алгебры……………………………………………………………………...6

1.1. Определение * - алгебры……………………………………………………….6

1.2. Примеры…………………………………………………………………………7

1.3. Алгебры с единицей…………………………………………………………….7

1.4. Простейшие свойства * - алгебр……………………………………………….9

1.5. Гомоморфизм и изоморфизм алгебр…………………………………………11

§ 2. Представления ……………………………………………………………….13

2.1. Определение и простейшие свойства представлений……………………….13

2.2. Прямая сумма представлений ………………………………………………..15

2.3. Неприводимые представления………………………………………………..16

2.4. Конечномерные представления……………………………………………….19

2.5. Интегрирование и дезинтегрирование представлений ……………………..20

§ 3. Тензорные произведения……………………………………………………26

3.1. Тензорные произведения пространств……………………………………….26

3.2. Тензорные произведения операторов………………………………………..28

Глава II . Задача о двух ортопроекторах………………………………………..31

§ 1. Два ортопроектора в унитарном пространстве…………………………..31

1.1. Постановка задачи……………………………………………………………..31

1.2. Одномерные *-представления *-алгебры  P₂……………………………….31

1.3. Двумерные *-представления *-алгебры  P₂……………………………….32

1.4. n-мерные *-представления *-алгебры  P₂…………………………………35

1.5. Спектральная теорема…………………………………………………………37

§ 2. Два ортопроектора в сепарабельном гильбертовом пространстве……39

2.1. Неприводимые *-представления *-алгебры  P₂…………………………...39

2.2. Спектральная теорема…………………………………………………………41

Глава III . Спектр суммы двух ортопроекторов ……………………………...45

§ 1. Спектр суммы двух ортопроекторов в унитарном пространстве……...45

1.1. Спектр ортопроектора в гильбертовом пространстве……………………….45

1.2. Постановка задачи……………………………………………………………..45

1.3. Спектр в одномерном пространстве………………………………………….45

1.4. Спектр в двумерном пространстве……………………………………….…..46

1.5. Спектр в n-мерном пространстве……………………………………………..47

1.6. Линейная комбинация ортопроекторов………………………………………49

Спектр суммы двух ортопроекторов в сепарабельном

гильбертовом пространстве …………………………………………………….52

2.1. Спектр оператора А = Р₁ +Р₂ …………………………………………………52

2.2. Спектр линейной комбинации А = аР₁ + bР₂ (0<а< b ) ……………………..53

Заключение………………………………………………………………………..55

Литература ………………………………………………………………………..56

 

ВВЕДЕНИЕ

Пусть Н – гильбертово пространство, L (Н) – множество непрерывных линейных операторов в Н. Рассмотрим подмножество А в L (Н), сохраняющееся при сложении, умножении, умножении на скаляры и сопряжении. Тогда А – операторная *-алгебра. Если дана абстрактная *-алгебра А, то одна из основных задач теории линейных представлений (*-гомоморфизмов А в L (Н)) – перечислить все ее неприводимые представления (с точностью до эквивалентности).

Теория унитарных представлений групп восходит к XIX веку и связана с именами Г.Фробениуса, И.Шура, В.Бернсайда, Ф.Э. Молина и др. В связи с предложениями к квантовой физике теория унитарных представлений топологических групп, групп Ли, С*-алгебр была разработана И.М.Гельфандом, М.А. Наймарком, И.Сигалом, Ж.Диксмье, А.А. Кирилловым и др. в 60-70-х годах XX века. В дальнейшем интенсивно развивается теория представлений *-алгебр, заданных образующими и соотношениями.

Дипломная работа посвящена развитию теории представлений (конечномерных и бесконечномерных) *-алгебр, порожденных двумя проекторами.

Глава I в краткой форме содержит необходимые для дальнейшего сведения из теории представлений и функционального анализа. В §1 дано определение *-алгебры и приведены простейшие свойства этих алгебр. В §2 излагаются основные свойства представлений, вводятся следующие понятия: неприводимость, эквивалентность, прямая сумма, интегрирование и дезинтегрирование представлений. В §3 определяются тензорные произведения пространств, тензорные произведения операторов и др. (см. [2], [3], [4], [8], [9])

В Главе II изучаются представления *-алгебры P₂

P₂= С < p ₁ , p ₂ | p ₁ ² = p ₁ * = p ₁ , p ₂ ² = p ₂ * = p ₂ >,

порожденной двумя самосопряженными идемпотентами, то есть проекторами (см., например, [12]). Найдены все неприводимые *-представления *-алгебры P₂, с точностью до эквивалентности., доказаны соответствующие спектральные теоремы.

В §1 рассматриваются только конечномерные *-представления π в унитарном пространстве Н. Описаны все неприводимые и неэквивалентные *-представления *-алгебры P₂ . Неприводимые *-представления P₂ одномерны и двумерны:

4 одномерных: π_0,0( p ₁ ) = 0, π_0,0( p ₂ ) = 0; π_0,1( p ₁ ) = 0, π_0,1( p ₂ ) = 1;

π_1,0( p ₁ ) = 1, π_1,0( p ₂ ) = 0; π_1,1( p ₁ ) = 1, π_1,1( p ₂ ) = 1.

И двумерные:  ,   τ  (0, 1).

Доказана спектральная теорема о разложении пространства Н в ортогональную сумму инвариантных относительно π подпространств Н, а также получено разложение π на неприводимые *-представления. Результаты §1 относятся к математическому фольклору.

В §2 получены основные результаты работы. Для пары проекторов в сепарабельном гильбертовом пространстве Н приведено описание всех неприводимых представлений, доказана спектральная теорема. 

В Главе III спектральная теорема для пары проекторов Р_1, Р₂, применяется к изучению сумм Р₁+Р₂, аР₁+ b Р₂ (0 < a < b ). Получены необходимое и достаточное условие на самосопряженный оператор А для того чтобы А = Р₁+Р₂ или А = аР₁+ b Р₂, 0 < a < b , (этот частный случай задачи Г.Вейля (1912 г.) о спектре суммы пары самосопряженных операторов).

 

Глава I . Основные понятия и определения

§ 1. - алгебры

1.1. Определение - алгебры.

Определение 1.1. Совокупность А элементов x , y , … называется алгеб-
рой, если:

1) А есть линейное пространство;

2) в А введена операция умножения (вообще некоммутативного), удовлет-
воряющая следующим условиям:

α (x y) = ( α x) y,

x ( α y) = α (x y),

(x y) z = x (y z),

(x + y) = xz +xy,

x ( y + z ) = xy + xz для любых x , y , z  А и любых чисел α.

Два элемента x , y алгебры А называются перестановочными, если xy = yx. Алгебра А называется коммутативной, если все ее элементы попарно пере-
становочны.

Определение 1.2. Пусть А – алгебра над полем С комплексных чисел. Инволюцией в А называется такое отображение x → x * алгебры А в А, что

(i) (x*)* = x;

(ii) (x + y)* = x* + y*;

(iii) ( α x)* =  x*;

(iv) ( x y )* = y * x *   для любых x , y  С.

Алгебра над С, снабженная инволюцией, называется инволютивной алгеброй или *- алгеброй. Элемент х* называют сопряженным к х. Подмножество А, сохраняющееся при инволюции, называется само-
сопряженным.

Из свойства ( i ) следует, что инволюция в А необходимо является биекцией А на А.

Примеры

1) На А = С отображение z →  (комплексное число, сопряженное к z) есть инволюция, превращающая С в коммутативную *- алгебру.

2) Пусть Т – локально компактное пространство, А = С(Т) – алгебра непре-
рывных комплексных функций на Т, стремящихся к нулю на бесконечности (то есть для любого ε > 0 множество {t T: |f ( t )|  ε} компактно, f ( t )  А. Снабжая А отображением f →  получаем коммутативную *- алгебру. Если Т сводится к одной точке, то возвращаемся к примеру 1).

3) Пусть Н – гильбертово пространство. А = L ( H ) – алгебра ограниченных линейных операторов в Н. Зададим инволюцию как переход к сопряженному оператору. Тогда А - *- алгебра.

4) Обозначим через К(Н) совокупность всех компактных операторов в гильбертовом пространстве Н; операции сложения, умножения на число и умножения определим как соответствующие действия с операторами. Тогда К(Н) будет *- алгеброй, если ввести инволюцию А→А* (А К(Н)). Алгебра К(Н) в случае бесконечного Н есть алгебра без единицы. Действительно, если единичный оператор I принадлежит К(Н), то он переводит открытый единичный шар S H в себя. Значит I не может быть компактным оператором.

5) Обозначим через W совокупность всех абсолютно сходящихся рядов .

Алгебра W есть *- алгебра, если положить . ( )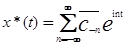

Алгебры с единицей

Определение 1.3. Алгебра А называется алгеброй с единицей, если А содержит элемент е, удовлетворяющий условию

ех = хе = х для всех х 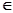А                                                                  (1.1.)

Элемент е называют единицей алгебры А.

Теорема 1.1. Алгебра А не может иметь больше одной единицы.

Доказательство. Действительно, если е΄ - также единица в А, то

е΄х = хе΄ = х, для всех х 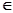А                                                                  (1.2.)

Полагая в (1.1.) х = е΄, а в (1.2.) х = е, получим:

ее΄ = е΄е = е΄ и е΄е = ее΄ =е, следовательно е΄ = е.

Теорема 1.2. Всякую алгебру А без единицы можно рассматривать как подалгебру некоторой алгебры А΄ с единицей.

Доказательство. Искомая алгебра должна содержать все суммы х΄=αе + х, х 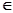А; с другой стороны, совокупность всех таких сумм образует алгебру А΄, в которой основные операции определяются формулами:

β(αе + х) = βαе + βх, (α₁е + х₁) + (α₂е + х₂) = (α₁ + α₂)е + (х₁ + х₂),

(α₁ е + х₁)(α₂ е+ х₂ )=α₁ α₂ е +α₁ х₂ +α₂ х₁ + х₁ х₂                                                                (1.3.)

Каждый элемент х΄ из А΄ представляется единственным образом в виде

х΄ = αе + х, х 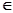А, так как по условию А не содержит единицы. Поэтому А΄ можно реализовать как совокупность всех формальных сумм х΄ = αе + х, х 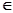А, в которой основные операции определяются формулами (1.3.); сама алгебра А получится при α = 0.

Алгебру А΄ можно также реализовать как совокупность всех пар (α, х), х А, в которой основные операции определяются по формулам:

β (α, х) = (βα, βх), (α₁, х₁) + (α₂, х₂) = (α₁ + α₂, х₁ + х₂),

(α₁, х₁)(α₂, х₂) = (α₁α₂, α₁х₂ + α₂ х₁ + х₁х₂),                                                       (1.4.)

аналогично тому, как определяются комплексные числа. Саму алгебру А можно тогда рассматривать как совокупность всех пар (0, х), х 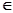А и не делать различия между х и (0, х). Полагая е = (0, х), мы получим:

(α, х) = α(1, 0) + (0, х) = αе + х,

так что вторая реализация алгебры А΄ равносильна первой.

Переход от А к А΄ называется присоединением единицы.

Определение 1.4. Элемент y называется левым обратным элемента х, если xy = e. Элемент z называется правым обратным элемента х, если xz = e.

Если элемент х имеет и левый, и правый обратные, то все левые и правые обратные элемента х совпадают. Действительно, умножая обе части равенства yx = e справа на z, получим

z = (yx)z = y(xz) = ye,

В этом случае говорят, что существует обратный х^-1 элемента х.

 

1.4. Простейшие свойства 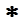- алгебр

Определение 1.5. Элемент х *-алгебры А называется эрмитовым или самосопряженным, если х* = х, нормальным, если хх* = х*х. Идемпотентный эрмитов элемент называется проектором. Элемент алгебры называется идемпотентным, если все его (натуральные) степени совпадают.

Каждый эрмитов элемент нормален. Множество эрмитовых элементов есть вещественное векторное подпространство А. Если х и y эрмитовы, то ( xy )*= y * x * = yx; следовательно, xy эрмитов, если x и y перестановочны. Для каждого х А элементы хх* и х*х эрмитовы. Но, вообще говоря, эрмитов элемент не всегда представим в этом виде, как показывает пример 1 из пункта 1.2. Действительно, для любого z C , но если z действительно отрицательное число, то его нельзя представить в виде .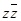

Теорема 1.3. Всякий элемент х *-алгебры А можно представить, и притом единственным образом, в виде х = х₁ + i х₂, где х₁, х₂ – эрмитовы элементы.

Доказательство. Если такое представление имеет место, то х* = х₁ + i х₂, следовательно:

,                                                                             (1.5.)

Таким образом, это представление единственно. Обратно, элементы х₁, х₂, определенные равенством (1.5.), эрмитовы и х = х₁ + i х₂.

Эти элементы х₁, х₂ называются эрмитовыми компонентами элемента х.

Заметим, что          хх* = х₁² + х₂² + i (х₂х₁ – х₁х₂),

хх* = х₁² + х22 - i (х₂х1 – х1х2)

так что х нормален тогда и только тогда, когда х₁ и х₂ перестановочны.

Так как е*е = е* есть эрмитов элемент, то е* = е , то есть единица эрмитов элемент.

Если А - *-алгебра без единицы, а А΄ - алгебра, полученная из А присоединением единицы, то, положив  при х А, мы определим инволюцию в А΄, удовлетворяющую всем требованиям определения 2. Так что А΄ станет *-алгеброй. Говорят, что А΄ есть *-алгебра, полученная из А присоединением единицы.

Теорема 1.4. Если х^-1 существует, то (х*)^-1 также существует и

(х*)^-1 = (х^-1)*

Доказательство. Применяя операцию * к обеим частям соотношения

х^-1х = хх^-1 = е,

получим х*(х^-1)*= (х*)^-1х*=е.

Но это означает, что (х^-1)* есть обратный к х*.

Подалгебра А₁ алгебры А называется *-подалгеброй, если из х А₁  следует, что х* А₁ .

Непустое пересечение *-подалгебр есть также *-подалгебра. В частности, пересечение всех *-поалгебр, содержащих данное множество S  А, есть минимальная *-подалгебра, содержащая S .

Коммутативная *-алгебра называется максимальной, если она не содержится ни в какой другой коммутативной *-подалгебре.

Теорема 1.5. Если В – максимальная коммутативная *-подалгебра, содержащая нормальный элемент х , и если х^-1 существует, то х^-1 В.

Доказательство. Так как х т х* перестановочны со всеми элементами из В, то этим же свойством обладают х^-1 и (х*)^-1 = (х^-1)*. В силу максимальности В отсюда следует, что х^-1 В.

Определение 1.6. Элемент х А - *-алгебры называется унитарным, если хх* = х*х = е, иначе говоря, если х обратим и х = (х*)^-1.

В примере 1 п.1.2. унитарные элементы – комплексные числа с модулем, равным 1.

Унитарные элементы А образуют группу по умножению – унитарную группу А. Действительно, если x и y – унитарные элементы *-алгебры А, то

((х y )*)^-1 = (у*х*)^-1 =(х*)^-1 (y *)^-1 = xy,

поэтому xy унитарен, и так как ((х^-1)*)^-1= ((х*)^-1)^-1 = х^-1, то х^-1 унитарен.

 

Гомоморфизм и изоморфизм алгебр

Определение 1.7. Пусть А и В – две *-алгебры. Назовем гомоморфизмом (*-гомоморфизмом) А в В такое отображение f множества А в В, что

f (x + y) = f (x) + f (y),

f (αx) = α f (x),

f (xy) = f (x) f (y),

f (x*) = f (x)*

для любых х, y А, α С. Если отображение f биективно, то f называют изоморфизмом (*-изоморфизмом).

Определение 1.8. Совокупность I элементов алгебры А называется левым идеалом, если:

(i) I ≠ A;

(ii) Из х, y I следует x + y I;

(iii) Из х I, аα А следует  α х I .

Если I = А, то I называют несобственным идеалом.

Аналогично определяется и правый идеал. Идеал, являющийся одновременно и левым, и правым, называется двусторонним.

Всякий идеал автоматически оказывается алгеброй.

Пусть I – двусторонний идеал в алгебре А. Два элемента х, y из А назовем эквивалентными относительно идеала I, если х- y I. Тогда вся алгебра А разбивается на классы эквивалентных между собой элементов. Обозначим через А совокупность всех этих классов. Введем в А₁ операции сложения, умножения на число и умножения, производя эти действия над представителями классов. Так как I – двусторонний идеал, то результат операций не зависит от выбора этих представителей.

Следовательно, А₁  становится алгеброй. Эта алгебра называется фактор-алгеброй алгебры А по идеалу I и обозначается A / I.

*-гомоморфизм алгебр описывается при помощи так называемых самосопряженных двусторонних идеалов.

Определение 1.9. Идеал I (левый, правый или двусторонний) называется самосопряженным, если из х I следует х* I.

Самосопряженный идеал автоматически является двусторонним. Действительно, отображение х → х* переводит левый идеал в правый и правый идеал в левый; если поэтому отображение х → х* переводит I в I, то I есть одновременно и левый и правый идеал.

В фактор-алгебре A / I по самосопряженному двустороннему идеалу I можно определить инволюцию следующим образом. Если х- y I, то х*- y * I. Поэтому при переходе от х к х* каждый класс вычетов х по идеалу I переходит в некоторый другой класс вычетов по I. Все условия из определения 1.2. выполнены; следовательно, A / I есть *-алгебра.

Если х → х΄ есть *-гомоморфизм А на А΄, то полный прообраз I нуля (то есть ядро данного гомоморфизма) есть самосопряженный двусторонний идеал в А. Фактор-алгебра A / I *-изоморфна *-алгебре А΄.

Обратно, отображение х → [х]  каждого элемента х А в содержащий его класс вычетов по I есть *-гомоморфизм алгебра А на A / I.

 

Представления