 |
Главная |
Спектр суммы двух ортопроекторов в сепарабельном гильбертовом пространстве
|
из
5.00
|
2.1. Спектр оператора А = Р1 + Р2. Изучим оператор Р1 + Р2 в сепарабельном гильбертовом пространстве.
Теорема 2.1. Самосопряженный оператор А представим в виде суммы двух ортопроекторов А = Р1 + Р2 тогда и только тогда, когда  (А) = [0, 2] и пространство Н можно разложить в ортогональную сумму инвариантных относительно А пространств
(А) = [0, 2] и пространство Н можно разложить в ортогональную сумму инвариантных относительно А пространств
Н = Н0 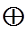 Н1
Н1 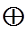 Н2
Н2  (
(  (С2
(С2  L2((0,
L2((0,  ), dρк))) (2.1.)
), dρк))) (2.1.)
и меры ρк инвариантны относительно преобразования 1+х → 1-х.
Доказательство. Пусть А = Р1 +Р2. Н0=Н0,0 , Н1=Н1,0 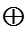 Н0,1 , Н2=Н1,1
Н0,1 , Н2=Н1,1
Поставим в соответствие φ→ε cosφ, где φ  (0,
(0,  ). Тогда, как было найдено выше, спектр
). Тогда, как было найдено выше, спектр  (А)
(А) 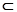 [0, 2] и Н можно разложить (опираясь на спектральную теореме 2.3. главы II) в ортогональную сумму (2.1.)
[0, 2] и Н можно разложить (опираясь на спектральную теореме 2.3. главы II) в ортогональную сумму (2.1.)
Н = Н0 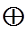 Н1
Н1 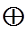 Н2
Н2  (
(  (С2
(С2  L2((0, 2), dρк)))
L2((0, 2), dρк)))
Поскольку собственные подпространства, соответствующие собственным значениям А 1+ε , 1-ε, 0<ε<1 входят одновременно в спектр и их значения совпадают, то каждая мера ρк (к = 1, 2, …) должна быть инвариантной относительно преобразования 1 + х → 1- х.
Обратно. Пусть имеет место (2.1.) и  (А)
(А) 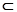 [0, 2]. Тогда зададим ортопроекторы Р1΄ Р2΄ равенствами
[0, 2]. Тогда зададим ортопроекторы Р1΄ Р2΄ равенствами
Р1΄ = P1  P2
P2  (
(  (
( 
 Iк ))
Iк ))
Р2΄ = P2  (
( 

 Iк ))
Iк ))
где Pi: Н→Нi (i = 0, 1, 2) ортопроектор, Ik – единичный оператор в L2((0, 2), dρк)). Тогда А =Р1΄ + Р2΄ - самосопряженный оператор, спектр которого содержится в [0, 2], так как Рк΄ (к = 1, 2) является суммой ортопроекторов на взаимно ортогональные пространства.
2.2. Спектр линейной комбинации А = aР1 + bР2 (0<a<b). Рассмотрим теперь случай, когда А = aР1 + bР2 (0<a<b).
Теорема 2.2. Самосопряженный оператор А представим в виде линейной комбинации двух ортопроекторов А = aР1 + bР2, 0<a<b тогда и только тогда, когда  (А)
(А) 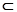 [0, a]
[0, a] 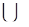 [b, a+ b] и Н можно представить в виде ортогональной суммы инвариантных относительно А пространств
[b, a+ b] и Н можно представить в виде ортогональной суммы инвариантных относительно А пространств
Н = Н0  Н a
Н a  Н b
Н b  Н a+ b
Н a+ b  (
(  (С2
(С2  L2([0, a]
L2([0, a] 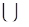 [b, a+ b], dρк)))) (2.2.)
[b, a+ b], dρк)))) (2.2.)
и меры ρк инвариантны относительно преобразования х→ a+ b.
Доказательство. Пусть А = aР1 + bР2 (0<a<b). Пусть Н0=Н0,0, На=Н0,1, Н b=Н1,0 , Н a+ b=Н1,1. Так как  (А)
(А) 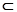 [0, a]
[0, a] 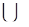 [b, a+ b] и собственные подпространства, отвечающие собственным значениям оператора А входят в Н одновременно (причем их размерности совпадают) то аналогично теореме 2.1. получаем
[b, a+ b] и собственные подпространства, отвечающие собственным значениям оператора А входят в Н одновременно (причем их размерности совпадают) то аналогично теореме 2.1. получаем
Н = Н0  Н a
Н a  Н b
Н b  Н a+ b
Н a+ b  (
(  (С2
(С2  L2([0, a]
L2([0, a]  [b, a+ b], dρк))))
[b, a+ b], dρк))))
где меры ρк (к = 1, 2, …) инвариантны относительно преобразования х → a+ b-х.
Обратно, пусть  (А)
(А) 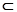 [0, a]
[0, a] 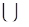 [b, a+ b] и имеется разложение Н (2.2.). Тогда зададим Р1 и Р2 следующим образом
[b, a+ b] и имеется разложение Н (2.2.). Тогда зададим Р1 и Р2 следующим образом
P1 = Pa  Pa+b
Pa+b  (
(  (
( 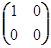
 I к ))
I к ))
Р 2 = Pb  Pa+b (
Pa+b ( 

 I к ))
I к ))
где Рα: Н→Н α , α = a, b, a+ b – ортопроекторы, Iк – единичный оператор в L2([0,a]  [b, a+ b]). Тогда
[b, a+ b]). Тогда
А = aР 1 + bР 2 = aР 1  bР 2
bР 2  (a+b)Pa+b
(a+b)Pa+b  (
(  (
( 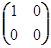
 I к ))
I к )) 
 (
( 

 Iк ))
Iк ))
ЗАКЛЮЧЕНИЕ
В дипломной работе изучена пара ортопроекторов в сепарабельном гильбертовом пространстве Н, приведено описание всех неприводимых и неэквивалентные *-представления *-алгебры P2 .
P2 = С <p1, p2 | pк2 = pк* =pк>.
А именно: 4 одномерных π0,0(p1) = 0, π0,0(p2) = 0; π0,1(p1) = 0, π0,1(p2) = 1; π1,0(p1) = 1, π1,0(p2) = 0; π1,1(p1) = 1, π1,1(p2) = 1.
И двумерные:  ,
,  τ
τ  (0, 1)
(0, 1)
Изучен спектр операторов Р1 + Р2, aР1 + bР2 (0<a<b), а также необходимые и достаточные условия представимости самосопряженного оператора А в виде А = Р1 + Р2 и А = aР1 + bР2 (0<a<b).
ЛИТЕРАТУРА
1. Ахиезер Н.И., Глазман И.М. Теория линейных операторов в гильбертовом пространстве, М., Наука, 1966.
2. Березенский Ю.М., Ус Г.Ф., Шефтель З.Г. Функциональный анализ, К., Выща школа, 1990.
3. Браттели У., Робинсон Д. Операторные алгебры и квантовая статистическая механика: С*- W* -алгебры. Группы симметрий. Разложение состояний., М., Мир, 1982.
4. Диксмье Ж. С*-алгебры и их представления. М., Наука, 1974.
5. Кириллов А.А. Элементы теории представлений. М., Наука, 1978.
6. Кужель А.В. Алгебры конечного ранга, С. СГУ, 1979.
7. Ленг С. Алгебра. М., Мир, 1968.
8. Мерфи Д. С*-алгебры и теория операторов. М., Мир, 1998.
9. Наймарк М.А. Нормированные кольца. М., Гостехиздат, 1956.
10. Рудин У. Функциональный анализ. М., Мир, 1975.
11. NishioK, Linear algebra and its applications 66: 169-176, Elsevier Science Publishing Co., Inc., 1985.
12. Samoilenko Y.S., Representation theory of algebras, Springer, 1998.
|
из
5.00
|
Обсуждение в статье: Спектр суммы двух ортопроекторов в сепарабельном гильбертовом пространстве |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

