 |
Главная |
Тензорные произведения пространств
|
из
5.00
|
3.1. Тензорные произведения пространств. Пусть  - конечная последовательность сепарабельных гильбертовых пространств,
- конечная последовательность сепарабельных гильбертовых пространств,  - некоторый ортонормированный базис в Нк.
- некоторый ортонормированный базис в Нк.
Образуем формальное произведение
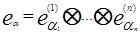 (3.1.)
(3.1.)
α = (α1,…, αn) 
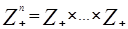 (n раз), то есть рассмотрим упорядо-
(n раз), то есть рассмотрим упорядо-
ченную последовательность (  ) и на формальные векторы (3.1.) натянем гильбертово пространство, считая, что они образуют его ортонормиро-
) и на формальные векторы (3.1.) натянем гильбертово пространство, считая, что они образуют его ортонормиро-
ванный базис. Полученное сепарабельное гильбертово пространство называется тензорным произведением пространств Н1,…, Н n и обозначается Н1  ,…,
,…,  Н n =
Н n = 
 . Его векторы имеют вид:
. Его векторы имеют вид:
f=  (f α
(f α  C), || f||2 =
C), || f||2 =  < ∞ (3.2.)
< ∞ (3.2.)
Пусть g= 


 , тогда скалярное произведение опреде-
, тогда скалярное произведение опреде-
ляется формулой
( f, g) =  (3.3.)
(3.3.)
Пусть f( k)= 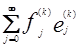

 (к = 1,…, n) – некоторые векторы. По определению
(к = 1,…, n) – некоторые векторы. По определению
f = f(1)  …
…  f(n) =
f(n) =  (3.4.)
(3.4.)
Коэффициенты f α =  разложения (3.4.) удовлетворяют условию (3.2.), поэтому вектор (3.4.) принадлежит
разложения (3.4.) удовлетворяют условию (3.2.), поэтому вектор (3.4.) принадлежит 
 , при этом
, при этом
|| f || =  (3.5.)
(3.5.)
Функция Н1  ,…,
,…,  Н n
Н n  <
<  >
> 



 линейна по каждому фрагменту, а линейная оболочка L векторов (3.4.) плотна в
линейна по каждому фрагменту, а линейная оболочка L векторов (3.4.) плотна в 
 - эта линейная оболочка называется алгебраическим (непополненным) тензорным произведением пространств Н1,…, Н n и обозначается α.
- эта линейная оболочка называется алгебраическим (непополненным) тензорным произведением пространств Н1,…, Н n и обозначается α. 

Приведенное определение тензорного произведения зависит от выбора ортогонального базиса  в каждом сомножителе
в каждом сомножителе  . При изменении базисов получаем тензорное произведение, изоморфное с сохранением своей структуры исходному произведению.
. При изменении базисов получаем тензорное произведение, изоморфное с сохранением своей структуры исходному произведению.
Пусть Н1 и Н2 – гильбертовы сепарабельные пространства. Тогда конструкция тензорного произведения означает следующее. Рассматривается линейная оболочка L формальных произведений f1  f2, причем считается, что
f2, причем считается, что
(f1 + g1)  f2 = f1
f2 = f1  f2 + g1
f2 + g1  f2 (3.6.)
f2 (3.6.)
f1  (f2 + g2) = f1
(f2 + g2) = f1  f2 + f1
f2 + f1  g2 (3.7.)
g2 (3.7.)
(λ f1) 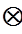 f2=λ (f1
f2=λ (f1  f2) (3.8.)
f2) (3.8.)
f1  λ (f2) = λ (f1
λ (f2) = λ (f1  f2) (3.9.)
f2) (3.9.)
f1, g1  Н1; f2, g2
Н1; f2, g2  Н2; λ
Н2; λ  С.
С.
Иными словами, линейное пространство L факторизируется по его линейному подмножеству, натянутому на всевозможные векторы, имеющие вид разностей между правыми и левыми частями равенств (3.6.) – (3.9.).
Затем вводится скалярное произведение в L.
(f1  f2 , g1
f2 , g1  g2 ) = (f1 g1)(f2 g2) (3.10.)
g2 ) = (f1 g1)(f2 g2) (3.10.)
f1, g1  Н1; f2, g2
Н1; f2, g2  Н2,
Н2,
а затем распространяется на другие элементы из факторизованного L билинейным образом.
3.2. Тензорные произведения операторов. Определим тензорное произведение ограниченных операторов.
Теорема 3.1. Пусть 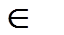 ,
,  - две последовательности гильбер-
- две последовательности гильбер-
товых пространств,  - последовательность операторов Ак
- последовательность операторов Ак  L(Нк, Gк). Определим тензорное произведение А1
L(Нк, Gк). Определим тензорное произведение А1  …
…  А n =
А n =  Ак формулой
Ак формулой
( 
 ) f =
) f = 
 (
(  ) =
) =  (3.11.)
(3.11.)
(f 

 ).
).
Утверждается, что ряд в правой части (3.11.) сходится слабо в 
 и определяет оператор
и определяет оператор 

 L (
L ( 
 ,
, 
 ), причем
), причем
|| 
 || =
|| =  ||
||  || (3.12.)
|| (3.12.)
Доказательство. Достаточно рассмотреть случай n=2, так как в силу равенства Н1  ,…,
,…,  Н n = (Н1
Н n = (Н1  ,…,
,…,  Н n-1)
Н n-1)  Н n общий случай получается по индукции.
Н n общий случай получается по индукции.
Пусть  - некоторый ортонормированный базис в Gк (к = 1, 2) и пусть g =
- некоторый ортонормированный базис в Gк (к = 1, 2) и пусть g = 
 G1
G1  G2. В качестве f возьмем вектор из Н1
G2. В качестве f возьмем вектор из Н1  Н2 с конечным числом отличных от нуля координат fα.
Н2 с конечным числом отличных от нуля координат fα.
Зафиксируем α2, β1  Z+ и обозначим через f(α2)
Z+ и обозначим через f(α2)  Н1 вектор f(α2) =
Н1 вектор f(α2) =  и через g(β1)
и через g(β1)  G2 – вектор g(β1) =
G2 – вектор g(β1) =  . Получим
. Получим
 =
= 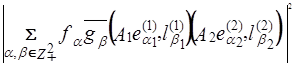 =
=
=  ≤
≤  =
=
=  ≤
≤  =
=
= 
Из этого неравенства следует слабая сходимость в G1  G2 ряда
G2 ряда  уже при произвольном c
уже при произвольном c  Н1
Н1  Н2 и оценка его нормы в G1
Н2 и оценка его нормы в G1  G2 сверху через ||A1|| ||A2|| ||f||. Таким образом, оператор A1
G2 сверху через ||A1|| ||A2|| ||f||. Таким образом, оператор A1  A2: Н1
A2: Н1  Н2 →G1
Н2 →G1  G2 определен посредством (3.11.) корректно, ограничен и его норма не превосходит ||A1|| ||A2||.
G2 определен посредством (3.11.) корректно, ограничен и его норма не превосходит ||A1|| ||A2||.
Из (3.5.) и (3.11.) следует
||(A1  A2) (f1
A2) (f1  f2)|| = ||A1 f1||||A2 f2|| (fк
f2)|| = ||A1 f1||||A2 f2|| (fк  Нк , к = 1, 2)
Нк , к = 1, 2)
Подбирая должным образом орты f1, f2 последнее произведение можно сделать сколь угодно близким к ||A1|| ||A2||, поэтому неравенство ||(A1  A2)|| ≤ ||A1|| ||A2|| не может выполняться, то есть (3.12.) при n=2 доказано.
A2)|| ≤ ||A1|| ||A2|| не может выполняться, то есть (3.12.) при n=2 доказано.
Из (3.11.) получаем для Ак  L(Hк, Gк), Вк
L(Hк, Gк), Вк  L(Hк, Gк) (к = 1,…, n) соотношения
L(Hк, Gк) (к = 1,…, n) соотношения
(  Вк) (
Вк) (  Ак) =
Ак) =  (Вк Ак) (3.13.)
(Вк Ак) (3.13.)
(  Ак)* =
Ак)* =  Ак* (3.14)
Ак* (3.14)
(  Ак) (f1
Ак) (f1  …
…  f n) = A1 f1
f n) = A1 f1  …
…  An fn (3.15.)
An fn (3.15.)
(fк  Hк; к = 1,…, n)
Hк; к = 1,…, n)
(3.15) однозначно определяет оператор  Ак.
Ак.
Приведем пример. Пусть Hк = L2(  (0,1), d (
(0,1), d (  mк)) = L2
mк)) = L2
Действительно, вектору вида (3.1.) 

 поставим в соответствие функцию
поставим в соответствие функцию 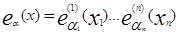
 L2. Такие функции образуют ортонормированный базис пространства L2, поэтому такое соответствие порождает требуемый изоморфизм между
L2. Такие функции образуют ортонормированный базис пространства L2, поэтому такое соответствие порождает требуемый изоморфизм между 
 и L2.
и L2.
|
из
5.00
|
Обсуждение в статье: Тензорные произведения пространств |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

