Конечномерные представления.

Теорема 2.7. Пусть π – конечномерное представление *-алгебры А. Тогда π = π₁ ….. π_n , где π_i неприводимы.

Доказательство. Если dimπ = 0 (n=0), то все доказано. Предположим, что dimπ = q и что наше предложение доказано при dimπ< q. Если π неприводимо, то предложение снова доказано. В противном случае π = π΄  π΄΄, причем dimπ΄<q, dimπ΄΄<q, и достаточно применить предположение индукции.

Разложение π = π₁ ….. π_n  не единственно. Тем не менее, мы получим некоторую теорему единственности.

Пусть ρ₁, ρ₂ – два неприводимых подпредставления π. Им отвечают инвариантные подпространства Н₁ и Н₂. Пусть Р₁ и Р₂ – проекторы Н на Н₁ и Н₂. Они коммутируют с π(А). Поэтому ограничение Р₂ на Н₁ есть оператор, сплетающий ρ₁ и ρ₂. Следовательно, если Н₁ и Н₂ не ортогональны, то из пункта 2.3. следует, что ρ₁ и ρ₂ эквивалентны. Это доказывает, что любое неприводимое подпредставление π эквивалентно одному из π_i . Итак, перегруп-
пировав π_i , получаем, что π = ν ₁ ….. ν _m, где каждое ν _i есть кратное ρ _i ν _i ΄ неприводимого представления ν _i ΄, и ν _i ΄ попарно эквивалентны. Если ρ – неприводимое представление π, то предыдущее рассуждение показывает, что соответствующее инвариантное подпространство Н΄ ортогонально всем инвариантным подпространствам Н_i, отвечающих ν _i, кроме одного. Поэтому Н΄ содержится в одном из Н_i. Это доказывает, что каждое пространство Н_i определяется однозначно: Н_i – это подпространство Н, порожденное пространствами подпредставлений π, эквивалентных ν _i ΄. Таким образом, доказано предложение.

Теорема 2.8. В разложении π = ρ₁ν ₁ ΄ ….. ρ_mν _m ΄ представления π, (где ν ₁ ΄,…, ν _m ΄ неприводимы и неэквивалентны) целые числа ρ _i и классы представлений ν _i ΄ определяются единственным образом, как и пространства представлений.

2.5. Интегрирование и дезинтегрирование представлений. Напомним определение борелевского пространства.

Определение 2.7. Борелевским пространством называется множество Т, снабженное множеством В подмножеств Т, обладающим следующими свойствами: Т В, Ø 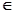В, В инвариантно относительно счетного объединения, счетного пересечения и перехода к дополнению.

Определение 2.8. Пусть Т₁, Т₂ – борелевские пространства. Отображение f : Т₁→Т₂ называется борелевским, если полный прообраз относительно f любого множества в Т₂ есть борелевское множество в Т₁.

Дадим несколько вспомогательных определений и утверждений.

Пусть Т – борелевское пространство и μ – положительная мера на Т.

Определение 2.9. μ – измеримое поле гильбертовых пространств на Т есть пара ε = ((H(t))_{t T}, Г), где (H(t))_{t T} – семейство гильбертовых пространств, индексы которых пробегают Т, а Г – множество векторных полей, удовлетворяющее следующим условиям:

(i) Г – векторное подпространство Н(t);

(ii) существует последовательность (х₁, х₂,…) элементов Г таких, что для любого t T элементы х _n ( t ) образуют последовательность H(t);

(iii) для любого х Г функция t →||x ( t )|| μ – измерима;

(iv) пусть х – векторное поле; если для любого y Г функция t →(x ( t ), y ( t )) μ – измерима, то х Г.

Пусть ε = ((H(t))_{t T}, Г) μ – измеримое поле гильбертовых пространств на Т. Векторное поле х называется полем с интегрируемым квадратом, если х Г и ||x( t)||² dμ( t) < +∞.

Если х, y – с интегрируемым квадратом, то х+ y и λх (λ С) – тоже и функция t →( x ( t ), y ( t )) интегрируема; положим

(x, y) = (x(t), y(t)) d μ (t)

Тогда векторные поля с интегрируемым квадратом образуют гильбертово пространство Н, называемое прямым интегралом Н( t ) и обозначаемое x ( t ) d μ( t ).

Определение 2.10. Пусть ε = ((H(t))_{t 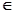T}, Г) – измеримое поле гильбер-
товых пространств на Т. Пусть для любого t 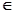T определен оператор S( t ) L(H( t )). Если для любого х T поле t →S( t ) x ( t ) измеримо, то t →S( t ) называется измеримым операторным полем.

Пусть Т – борелевское пространство, μ - положительная мера на Т, t →Н( t ) - μ - измеримое поле гильбертовых пространств на Т. Пусть для каждого t 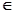T задано представление π( t ) *-алгебры А в Н( t ): говорят, что t →π( t ) есть поле представлений А.

Определение 2.11. Поле представлений t →π( t ) называется измеримым, если для каждого х А поле операторов t →π( t )х измеримо.

Если поле представлений t →π( t ) измеримо, то для каждого х А можно образовать непрерывный оператор π(х)= π( t ) ( x ) d μ( t ) в гильбертовом прост-
ранстве Н = Н( t ) dμ( t ).

Теорема 2.9. Отображение х→π(х) есть представление А в Н.

Доказательство. Для любых х, y 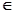А имеем

π(х+ y ) = π(t) (x+y) dμ( t ) = (π(t) (x) + π(t) (y)) dμ( t ) = π(t) (x )dμ( t ) +

+ π( t ) ( y ) d μ( t ) = π(х) +π( y )

Аналогично π(λх) = λπ(х), π(х y ) = π(х) π( y ), π(х*)=π(х)*

Определение 2.12. В предыдущих обозначениях  π называется прямым интегралом π( t ) и обозначается π = π(t) dμ( t ).

Определение 2.13. Операторное поле t →φ( t )I( t ) L ( H( t )) где I( t )-единичный оператор в H( t ), называется диагональным оператором в Н= Н( t )dμ( t ).

Пусть ε = ((H(t))_{t T}, Г) – μ-измеримое поле гильбертовых пространств на Т, μ₁ – мера на Т, эквивалентная μ (то есть каждая из мер μ₁, μ абсолютно непрерывна по другой), и ρ( t)= . Тогда отображение, которое каждому х Н== Н( t)dμ( t) составляет поле t→ρ( t^)-1/2х( t)Н₁= Н( t) dμ₁( t),

есть изометрический изоморфизм Н на Н₁, называемый каноническим.

Действительно,

|| ρ( t ^)-1/2х( t )dμ₁( t )||² = ||х( t )||²ρ( t ^)-1 dμ₁( t ) = ||х( t )||²dμ₁( t ) = ||х( t )||²

Теорема 2.10. Пусть Т – борелевское пространство, μ – мера на Т, t →Н( t ) – измеримое поле гильбертовых пространств на Т, t →π( t ) – измеримое поле представлений А в Н( t ),

Н = Н( t ) dμ( t ) , π₁== π(t )dμ( t ),

Д – алгебра диагональных операторов в Н. Пусть μ₁ – мера на Т, эквивалентная μ,

Н₁ = Н( t ) dμ₁( t ) , π₁ = π(t) dμ₁( t ),

Д₁ – алгебра диагональных операторов в Н₁. Тогда канонический изоморфизм преобразует π в π₁ и Д в Д₁.

Доказательство. Пусть ρ( t )= . Канонический изоморфизм из Н в Н₁ есть изометрический изоморфизм, который переводит х = x ( t ) d μ( t ) Н  в

Ux = ρ^-1/2х( t ) d μ₁( t ).

Пусть α А. Имеем

π₁ (α)Ux = π(t)(α) ρ^-1/2 х( t ) d μ₁( t ) = U π(t)(α) х( t ) d μ( t ) = Uπ(α)x,

поэтому и преобразуем π в π₁. Тогда если S Д, то аналогично SUx = USx, для любого х Н.

Определение 2.14. Пусть Т, Т₁ – борелевские пространства; μ, μ₁ – меры на Т и Т₁ соответственно; ε = ((H(t))_{t T}, Г), Z ₁ = ((H ₁(t ₁))_{t 1 T1}, Г), - μ-измеримое и μ₁-измеримое поля гильбертовых пространств. Пусть η: Т→Т₁ – борелевский изоморфизм, переводящий μ в μ₁; η-изоморфизм ε на ε₁ называется семейство (V(t))_{t T}, обладающееследующими свойствами:

(i) для любого t T отображение V( t ) является изоморфизмом Н( t ) на Н₁(η( t ));

(ii) для того, чтобы поле векторов t → x ( t ) H( t ) на Т было μ-измеримо, необходимо и достаточно, чтобы поле η( t )→V(t)х( t ) Н₁(η( t )) на Т₁ было μ₁-измеримо.

Отображение, переводящее поле х 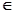Н = Н( t) dμ( t) в поле η( t))→V(t)х( t) Н₁ = Н₁( t) dμ₁( t) , есть изоморфизм Н на Н₁, обозначаемый V( t) dμ( t).

Теорема 2.11. Пусть Т – борелевское пространство; μ – мера на Т, t →H( t ) – μ- измеримое поле гильбертовых пространств на Т, t → π( t ) - μ- измеримое поле представлений А в H( t ),

Н = Н( t ) dμ( t ), π == π(t) dμ( t ),

Д – алгебра диагональных операторов в Н. Определим аналогичным образом Т₁, μ₁, t₁→H ₁( t₁), t₁→ π₁( t₁), Н₁,  π₁, Д₁.

Предположим, что существует:

1. N, N ₁ – борелевские подмножества Т и Т₁, такие что μ (N) = μ (N ₁) = 0;

2. борелевский изоморфизм η: T \ N →T \ N ₁, преобразует μ в μ₁;

3. η-изоморфизм t →V(t) поля t →Н(t) (t Z \ N) на поле t₁→Н₁(t₁) (t₁ Т₁\ N ₁) такой, что V(t) преобразует π( t ) в π₁(η( t )) для каждого t.

Тогда V = V( t)dμ( t) преобразует Д в Д₁ и π в π₁.

Доказательство. Обозначим через I_t, I_t1 единичные операторы в Н(t) и Н₁(t₁). Если f 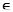L ^∞(T, μ) и если f₁ – функция на Т₁\ N ₁, получаемая из f|(T \ N) при помощи η, то V преобразует f ( t )I_t dμ( t ) в f₁( t₁) I_t1 dμ₁( t₁), поэтому V преоб-
разует Д в Д₁. С другой стороны, пусть α 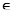А и х = х( t ) dμ( t ) Н.

Тогда 

Vπ(α)х = V π(t)(α) х( t ) d μ( t ) = V(η^-1(t₁)) π(η^-1(t₁))(α) х(η^-1(t₁)) d μ₁( t₁) = π₁(t₁)(α) V(η^-1(t₁)) х(η^-1(t₁)) d μ₁( t₁) = π₁ (α) V х

Поэтому V преобразует π в π₁.

Приведем примеры прямых интегралов.

1. Пусть имеется последовательность гильбертовых пространств  и дискретная мера μ на N, то есть μ( n )=1 для любого n N. Тогда

Н( n ) d μ( n ) = 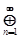Н( n ), то есть прямой интеграл сводится к ортогональ-
ной сумме.

2. Пусть Т=[0, 1] и в каждой точке t Т соответствует поле комплексных чисел С, и на Т задана линейная мера Лебега dt. Тогда С dt = L ₂ (0, 1).

Изоморфизм устанавливается отображением х = х( t) dt →х( t) L₂ (0, 1).

Разложения представления на неприводимые представления в прямой интеграл называют дезинтегрированием.