 |
Главная |
Два ортопроектора в унитарном пространстве
|
из
5.00
|
1.1. Постановка задачи. Пусть дана *-алгебра P2
P2 = С < р1, р2 | р12 = р1* = р1, р22 =р2* = р2 >
порожденная двумя проекторами, то есть двумя идемпотентными самосопряженными элементами.
Положим u = 2 p1 – 1, v = 2 p2 – 1, тогда u, v самосопряженные элементы.
u2 = (2p1 – 1)2 = 4p1 – 4p1 + 1 = 1, v2 = 1. Таким образом u, v – унитарные самосопряженные элементы.
Тогда *-алгебру P2 можно задать иначе:
P2 = С < p1*= p1, p2*=p2 | p12 = p1, p22 = p2 > = C <u* = u, v* = v | u2 = 1, v2 =1 >
Это групповая *-алгебра, порожденная двумя унитарными самосопряженными элементами.
Требуется найти все неприводимые представления *-алгебры P2 , с точностью до унитарной эквивалентности.
1.2. Одномерные *-представления *-алгебры P2 . Пусть π: P2 →L( H) - *-представление *-алгебры P2 . Рассмотрим сначала случай, когда dim H = 1, то есть dim π = 1.
P2 = С < р1, р2 | р12 = р1* = р1, р22 =р2* = р2 >
Обозначим через Рк = π(рк), к = 1,2. Поскольку рк2= рк* = рк (к = 1, 2) и π - *-представление, то Рк2 = Рк* = Рк (к =1, 2) – ортопроекторы в Н на подпространстве Нк = {y  H | Ркy = y } к = 1, 2.
H | Ркy = y } к = 1, 2.
Возможны следующие случаи:
1. Н1 = Н2 = {0}; тогда Р1 = 0, Р2 = 0.
2. Н1 = Н (то есть dim H1 =1), Н2 = {0}, тогда Р1 = 1, Р2 = 0.
3. Н1 = {0}, Н2 = Н (то есть dim H2 =1), тогда Р1 = 0, Р2 = 1.
4. Н1 = Н2 = Н (dim H1 = dim H2 =1), тогда Р1 = 1, Р2 = 1.
Так как dim H =1, то мы можем получить 4 одномерных неприводимых *-представлений P2, причем они неэквивалентны.
1.3. Двумерные *-представления *-алгебры P2 . Обозначим через Нк область значений оператора Рк при к = 1,2. Пусть Нк┴ - ортогональное дополнение подпространства Нк (к = 1,2) в Н. Тогда Н=H1  Н1┴ , Н=H2
Н1┴ , Н=H2  Н2┴
Н2┴
Введем дополнительные обозначения :
Н0,0 = Н1┴ ∩Н2┴, Н0,1 = Н1┴ ∩Н2, Н1,0 = Н1 ∩Н2┴, Н1,1 = Н1 ∩Н2. (1.1.)
Пусть dim H = 2. предположим, что существуют i и j такие, что Hij нетривиально, то есть dim Hij =1. Пусть, например, dim Н1,0 = 1 (остальные случаи аналогичны). Тогда в H существует ненулевой вектор h такой, что Н1,0 = л.о. {h}, но тогда P1h = h, P2h = 0; следовательно Н1,0 инвариантное подпространство. Значит в этом случае *-представление π не может быть неприводимым.
Будем считать, что Hij ={0} для любых i = 0, 1 и j =0, 1, (то есть Hij линейно независимы) и dim H1 = dim H2 =1. Тогда в Н можно найти два ортогональных базиса {e1, e2} и {g1, g2}, в которых матрицы операторов Р1 и Р2 имеют вид  . Найдем матрицу оператора Р2 в базисе {e1, e2}.
. Найдем матрицу оператора Р2 в базисе {e1, e2}.
 Пусть g1 = a11e1 + a12 e2
Пусть g1 = a11e1 + a12 e2
 g2 = a21e1 + a22e2
g2 = a21e1 + a22e2
e1 = b11g1 + b12g2
e2 = b21g1 + b22g2
Рассмотрим векторы h1 = eite1 и h2 = eile2, тогда
|| h1 || = || eite1 || = || e1 || = 1, || h2 || = || eile2 || = || e2 || = 1
(h1 , h2 ) = (eite1 , eile2) = ei( t- l)( e1, e2 ) = 0, то есть {h1 , h2} – ортонормированный базис.
Р1h1 =ei t Р1 e1 = h1, Р1h2 =eil Р1 e2 = 0.
Значит в базисе {h1 , h2} матрица оператора Р1 также имеет вид  . Тогда можно считать, что a11, a12 > 0 (так как, например, a11 e1=|a11| eite1 =|a11| h1)
. Тогда можно считать, что a11, a12 > 0 (так как, например, a11 e1=|a11| eite1 =|a11| h1)
(e1, e2 )= 0, значит a11 a21 = a12 a22 = 0 или 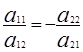 , тогда существует такое комплексное число r, что
, тогда существует такое комплексное число r, что
 a22 = - ra11
a22 = - ra11
a21 = ra12
Базис (e1, e2 ) ортонормированный; следовательно
 a112 + a122 = 1
a112 + a122 = 1
|a22 |2 + |a21 |2 = 0
тогда | r | = 1.
Р2 e1 = Р2 ( b11g1 + b12g2) = b11g1 = b11a11e1 + b11a12e2,
Р2 e2 = Р2 ( b21g1 + b22g2) = b21g1 = b21a11e1 + b21a12e2.
Найдем b11 и b21:
e1 = b11g1 + b12g2 = b11 (a11e1 + a12 e2) + b12 (a21e1 + a22e2) = (b11a11 + b12a12)e1 + (b11a12 + b12a22)e2,
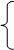 b11a11 + b12a12 = 1
b11a11 + b12a12 = 1
b11a12 + b12a22 = 0 или
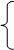 b11a11 + b12a12 r = 1
b11a11 + b12a12 r = 1
b11a12 - b12a11 r = 0,
Тогда b11 = a11.
Аналогично
E2 = b21g1 + b22g2 = (b21a11 + b22a21)e1 + (b21a12 + b22a22)e2,
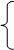 b21a11 + b22a21= 0
b21a11 + b22a21= 0
b21 a12 + b22 a22 = 1,
отсюда находим, что b21 = a12.
Тогда матрица оператора Р2 в базисе {e1, e2 } будет иметь вид (обозначим ее также через Р2)
Р2 =  , где a11>0, a12>0 и a112 + a122 =1
, где a11>0, a12>0 и a112 + a122 =1
А) Пусть a112 = τ, тогда a122 =1 – τ, a11a12 =  . Так как a11 a12 >0, то τ
. Так как a11 a12 >0, то τ  (0, 1).
(0, 1).
Тогда Р2 = 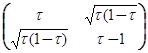 .
.
В) Положим a11 = cosφ,тогда a12 = sinφ и Р2 запишется следующим образом
Р2 =  .
.
Найдем коммутант π( P2). Пусть Т =  оператор перестановочный с Р1 и Р2, тогда
оператор перестановочный с Р1 и Р2, тогда
ТР1 = 
 =
= 
Р1Т = 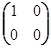
 =
= 
Следовательно b = c = 0.
ТР2 = 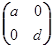
 =
= 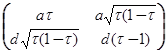
Р2Т= 
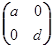 =
= 
Следовательно a = d. Тогда Т скалярный оператор и по лемме Шура (теорема 2.6. глава I) представление π неприводимо.
Покажем, что все эти представления неэквивалентны.
Пусть τ, ν  (0, 1), τ ≠ ν. Предположим, что существует унитарный оператор в Н, устанавливающий эквивалентность. Тогда
(0, 1), τ ≠ ν. Предположим, что существует унитарный оператор в Н, устанавливающий эквивалентность. Тогда
UР1 = Р1U, следовательно U=  , a, b
, a, b  C
C
UР2 (τ) = 
 =
= 
Р2 (ν) U = 
 =
=  .
.
Тогда τ = ν, следовательно U = 0 и представления неэквивалентны.
Теорема 1.1. Пусть π: P2 →L( H) - *-представление *-алгебры P2 .
Тогда:
( i) Все одномерные и неэквивалентные представления имеют вид: π0,0( p1) = 0; π0,0( p2) = 0; π1,0( p1) = 1; π1,0( p2) = 0; π0,1( p1) = 0; π0,1( p2) = 1; π1,1( p1) = 1; π1,1( p2) = 1;
( ii) Все двумерные неприводимые и неэквивалентные представления имеют вид: π( p1)  , π( p2)
, π( p2)  τ
τ  (0, 1).
(0, 1).
Доказательство следует из сказанного выше и в пункте (ii) можно положить π( p2) =  φ
φ  (0,
(0,  ).
).
1.4. n – мерные *-представления *-алгебры P2 . Рассмотрим случай нечетной размерности пространства Н. Если dimН=2n+1, где n>1 натуральное, то выполняется неравенство
max (dimН1, dimН1┴) + max (dimН2, dimН2┴) > 2n+1 (1.4.)
Тогда обязательно найдутся такие i = 0,1 и j= 0,1, что Н i, j ≠ {0}, следовательно, существует нетривиальное инвариантное подпространство относительно *-представления π, но тогда π приводимо.
Пусть теперь dimН=2n, n>1 натуральное. Будем считать, что dimН1 = n, dimН2 = n и Н i, j = {0} для любых i = 0,1 и j= 0,1, то есть Н i, j линейно независимы. Если это не так, то снова будет выполнятся неравенство (1.4.) и *-представление π окажется приводимым. При этих условиях справедлива лемма.
Лемма 1.1. Существует х ≠ 0, х 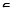 Н1 такой, что Р1Р2х = λх, где λ
Н1 такой, что Р1Р2х = λх, где λ  С.
С.
Доказательство. Пусть  ,
,  ортонормированный базисы в Н, в которых матрицы операторов Р1 и Р2 имеют вид
ортонормированный базисы в Н, в которых матрицы операторов Р1 и Р2 имеют вид  , где I – единичная матрица порядка n. Пусть базисы (е) и (g) связаны уравнениями
, где I – единичная матрица порядка n. Пусть базисы (е) и (g) связаны уравнениями

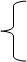


к = 1,…, n к = 1,…, n
Так как х  Н1, то
Н1, то  , gk
, gk  C, к = 1,…, n. Тогда
C, к = 1,…, n. Тогда
Р1Р2х = Р1Р2  = Р1Р2
= Р1Р2 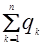
 = Р1
= Р1 
 =
=
= Р1 

 =
= 

 =
=  (
( 
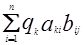 )
)  =
= 
Таким образом получаем систему линейных однородных уравнений относительно q1,…, qn:


 =
= 
j = 1,…, n
Подбирая λ  C так, чтобы определитель этой системы обратился в нуль, получим ненулевое решение q1,…, qn. Это доказывает лемму.
C так, чтобы определитель этой системы обратился в нуль, получим ненулевое решение q1,…, qn. Это доказывает лемму.
Лемма 1.2. Пусть элемент х удовлетворяет условиям леммы 15. Тогда L=л.о. {х, Р2х} – инвариантное подпространство в Н относительно Р1 и Р2.
Доказательство. Проверим инвариантность L. Для любых a, b  С имеем
С имеем
Р1 (aх + bР2х) = aх + λbх = (a + λb) х  L,
L,
Р2 (aх + bР2х) = aР2х + bР2х = (a + b) Р2х  L
L
dimL = 2, так как Н i, j = {0} (для всех i, j= 0,1).
Действительно, если aх + bР2х = 0, где, например, а ≠ 0, то х =  Р2х, значит
Р2х, значит  = 0 или 1 и х
= 0 или 1 и х  Н1,1; тогда Н1,1≠{0}.
Н1,1; тогда Н1,1≠{0}.
Итак, получаем предложение.
Теорема 1.2. Если dimН = n, n>2, то нет неприводимых *-пред-
ставлений *-алгебры P2 . Все неприводимые конечномерные *-представления одномерны и двумерны.
1.5. Спектральная теорема. Пусть dimН = n. В этом пункте мы получим разложение на неприводимые *-подпредставления исходного *-представления π *-алгебры P2, а также разложение пространства Н на инвариантные подпространства относительно π.
Теорема 3.1. (спектральная теорема). Существует единственное разложе-
ние Н в ортогональную сумму инвариантных относительно Р1 и Р2 подпространств
Н = Н0,0  Н0,1
Н0,1  Н1,0
Н1,0  Н1,1
Н1,1 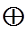 (
(  (С2
(С2  Нк)), (1.1.)
Нк)), (1.1.)
где каждому подпространству Нк соответствует одно φк  (0,
(0,  ), φк ≠ φ i при к≠i, dimНк = nк (к = 1,…, m). Пусть Рi,j: Н → Н i, j , Рφк: Н → С2
), φк ≠ φ i при к≠i, dimНк = nк (к = 1,…, m). Пусть Рi,j: Н → Н i, j , Рφк: Н → С2  Нк – ортопроекторы к = 1,…, m. Тогда существуют единственные разложения операторов
Нк – ортопроекторы к = 1,…, m. Тогда существуют единственные разложения операторов
I = P0,0 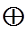 P0,1
P0,1 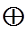 P1,0
P1,0 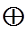 P1,1
P1,1 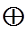 (
(  Рφк ), (1.2.)
Рφк ), (1.2.)
P1 = P1,0  P1,1
P1,1  (
(  (
( 
 Iк )) (1.3)
Iк )) (1.3)
Р 2 = P0,1 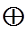 P1,1
P1,1  (
( 

 Iк )) (1.4)
Iк )) (1.4)
где Iк – единичный оператор на Нк (к = 1,…, m).
Доказательство. Пусть dimН i, j = ni, j. Сразу можем записать разложение
Н = Н0,0 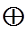 Н0,1
Н0,1 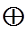 Н1,0
Н1,0 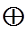 Н1,1
Н1,1  Н΄, где dimН΄ четное число. Используя лемму 1.2. и теорему 2.1. главы I можем написать разложение Н΄ в ортого-
Н΄, где dimН΄ четное число. Используя лемму 1.2. и теорему 2.1. главы I можем написать разложение Н΄ в ортого-
нальную сумму инвариантных двумерных подпространств, определяемых параметром φк  (0,
(0,  ):
):
Н΄ =  Нφк, (l = n -
Нφк, (l = n - 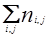 )
)
Собирая вместе все Нφк, у которых одно φк, получим изоморфизм
Нφк  …
…  Нφк ≈ С2
Нφк ≈ С2  Нк , где Нφк nк экземпляров, dim(Нφк
Нк , где Нφк nк экземпляров, dim(Нφк  …
…  Нφк )=2nк dim(С2
Нφк )=2nк dim(С2  Нк) = dimС2 dimНк = 2nк . Следовательно, получаем разложение (1.1.)
Нк) = dimС2 dimНк = 2nк . Следовательно, получаем разложение (1.1.)
Н = Н0,0  Н0,1
Н0,1  Н1,0
Н1,0  Н1,1
Н1,1  (
(  (С2
(С2  Нк))
Нк))
Пусть πi, j – сужение π на Н i, j ( i, j= 0,1), πк – сужение π на Нφк (к = 1,…, m), то есть πi, j и πк - *-подпредставления.
Учитывая кратности подпредставлений получаем
π = n0,0π0,0  n0,1π0,1
n0,1π0,1  n1,0π1,0
n1,0π1,0  n1,1π1,1
n1,1π1,1  (
(  nкπк) (1.5.)
nкπк) (1.5.)
В силу теоремы 2.8. главы I разложения (1.1.) и (1.5.) единственные.
Из (1.1.) следует разложение единичного оператора I (1.2.)
I = P0,0  P0,1
P0,1  P1,0
P1,0  P1,1
P1,1  (
(  Рφк)
Рφк)
Тогда ортопроекторы Р1 и Р2 примут вид
P1 = P1,0 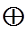 P1,1
P1,1 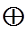 (
(  (
( 
 I к ))
I к ))
Р 2 = P0,1 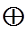 P1,1
P1,1  (
( 

 I к ))
I к ))
Причем n1,0π1,0(р 1) = P1,0 , n0,1π0,1(p2) = P0,1 , n1,1π1,1(р 1) = P1,1 , n0,0π0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно.
|
из
5.00
|
Обсуждение в статье: Два ортопроектора в унитарном пространстве |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

