 |
Главная |
Спектр ортопроектора в гильбертовом пространстве.
|
из
5.00
|
Теорема 1.1. Пусть Н – гильбертово пространство. Если Р – ортопроектор, то  (Р) =
(Р) =  р (Р) = {0, 1}, где
р (Р) = {0, 1}, где  р (Р) – точечный спектр при условии, что Р ≠ 0 и Р ≠ I.
р (Р) – точечный спектр при условии, что Р ≠ 0 и Р ≠ I.
Доказательство. Рассмотрим выражение Рх - λх = y, х, y 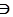 Н, λ
Н, λ 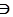 С. Тогда (1 - λ) Рх = Рy . Если λ ≠ 1, то Рх =
С. Тогда (1 - λ) Рх = Рy . Если λ ≠ 1, то Рх =  Рy. Если х ≠ 1, то х =
Рy. Если х ≠ 1, то х = 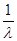 (
(  Рy - y), тогда
Рy - y), тогда  (Р) = {0, 1}.
(Р) = {0, 1}.
Так как Р ≠ 0 и Р ≠ I, то существует х ≠ 0 такой, что Рх ≠ 0. Тогда Р(Рх) = Рх, то есть 1 
 р (Р). Существует y ≠ 0: (I - Р)y ≠ 0, тогда Р(I - Р)y = 0 = 0 · (I - Р)y, то есть 0
р (Р). Существует y ≠ 0: (I - Р)y ≠ 0, тогда Р(I - Р)y = 0 = 0 · (I - Р)y, то есть 0 
 р (Р). Итак,
р (Р). Итак,  (Р) =
(Р) =  р (Р) = {0, 1}.
р (Р) = {0, 1}.
1.2. Постановка задачи. Пусть заданы два ортопроектора Р1 и Р2 в унитарном пространстве Н. Тогда мы знаем спектр каждого из них. Найдем спектр суммы Р1 + Р2 в неприводимых представлениях.
1.3. Спектр в одномерном пространстве. Пусть dimH =1. Пусть, как и выше, Нк – область значений оператора Рк к = 1,2. Обозначим через А = Р1 + Р2 и найдем  (А).
(А).
1) Р1 = Р2 = 0, то для любого х  Н Ах = 0 или Ах = 0 · х, то есть 0
Н Ах = 0 или Ах = 0 · х, то есть 0 
 (А).
(А).
2) Р1 = 0, Р2 = I, то для любого х  Н2 = Н Ах = х, то есть 1
Н2 = Н Ах = х, то есть 1 
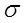 (А).
(А).
3) Р1 = I, Р2 = 0, то для любого х 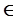 Н1 = Н Ах = х.
Н1 = Н Ах = х.
4) Р1 = Р2 = I, то для любого х  Н1 = Н2 = Н Ах = Р1х + Р2х = 2х, то есть 2
Н1 = Н2 = Н Ах = Р1х + Р2х = 2х, то есть 2 
 (А).
(А).
Таким образом, если dimH =1, то  (А)
(А)  {0, 1, 2}.
{0, 1, 2}.
1.4. Спектр в двумерном пространстве. Пусть dimH =2. Сохраним обозначения (1.1.) Главы II.
1) х  Н0,0 , тогда Ах = 0 и 0
Н0,0 , тогда Ах = 0 и 0 
 (А).
(А).
2) х  Н0,1 или х
Н0,1 или х  Н1,0 , тогда Ах = х и 1
Н1,0 , тогда Ах = х и 1 
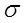 (А).
(А).
3) х  Н1,1, тогда Ах = 2х, то есть 2
Н1,1, тогда Ах = 2х, то есть 2 
 (А).
(А).
Если существуют i, j= 0,1 такие, что Н i, j ≠ {0}, то существуют k, l = 0,1 такие, что Н i, j  Н k, l = H. В этом случае
Н k, l = H. В этом случае  (А)
(А)  {0, 1, 2}.
{0, 1, 2}.
Пусть теперь Н k, l = {0} для любых k, l = 0,1. Допустим, что существует одномерное инвариантное подпространство L относительно Р1 и Р2, тогда АL  L. Пусть х
L. Пусть х  L, тогда Рkх = λкх (k = 1, 2 ). Так как Рk ортопроектор, то возможны случаи:
L, тогда Рkх = λкх (k = 1, 2 ). Так как Рk ортопроектор, то возможны случаи:
(i) λ1 = 0, λ2 = 0;
(ii) λ1 = 0, λ2 = 1;
(iii) λ1 = 1, λ2 = 0;
(iv) λ1 = 1, λ2 = 1;
Но это означает, что  k, l = 0,1 такие, что Н k, l ≠ {0} вопреки предположению. Тогда пара Р1, Р2 неприводима. Значит мы можем записать матрицы операторов Р1 и Р2 в некотором ортонормированном базисе, согласно теореме 1.1. главы II.
k, l = 0,1 такие, что Н k, l ≠ {0} вопреки предположению. Тогда пара Р1, Р2 неприводима. Значит мы можем записать матрицы операторов Р1 и Р2 в некотором ортонормированном базисе, согласно теореме 1.1. главы II.
Р1 =  , Р2
, Р2  τ
τ 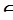 (0, 1)
(0, 1)
Найдем спектр линейной комбинации ортопроекторов aР1 + bР2, a и b 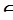 С. Для этого решим характеристическое уравнение det(aР1 + bР2 – λI) = 0.
С. Для этого решим характеристическое уравнение det(aР1 + bР2 – λI) = 0.

 (1.1.)
(1.1.)
Тогда  ,
,  (1.2)
(1.2)
Положим a = 1, b =1, ε =  , тогда λ1 = 1+ε , λ2 = 1-ε и 0<ε<1 (поскольку 0<τ<1.
, тогда λ1 = 1+ε , λ2 = 1-ε и 0<ε<1 (поскольку 0<τ<1.
Тогда  (А)
(А)  {0, 1, 2}
{0, 1, 2}  {1+ε , 1-ε}. Причем собственные значения 1+ε и 1-ε входят в спектр А одновременно.
{1+ε , 1-ε}. Причем собственные значения 1+ε и 1-ε входят в спектр А одновременно.
1.5. Спектр в n-мерном пространстве. Пусть dimH =n. Если Н =К  L, где К, L инвариантные подпространства относительно оператора А, то для любого х
L, где К, L инвариантные подпространства относительно оператора А, то для любого х  Н существует единственное разложение x = k +l, k
Н существует единственное разложение x = k +l, k  K, l
K, l  L. Пусть λ
L. Пусть λ 
 (А), тогда Ах = λх =λk +λl;, следовательно, если пространство Н разложено в ортогональную сумму инвариантных подпространств, то спектр оператора А можно найти как объединение спектров сужений оператора А на соответствующие инвариантные подпространства.
(А), тогда Ах = λх =λk +λl;, следовательно, если пространство Н разложено в ортогональную сумму инвариантных подпространств, то спектр оператора А можно найти как объединение спектров сужений оператора А на соответствующие инвариантные подпространства.
Используя лемму 1.2. главы II, представим Н в виде ортогональной суммы подпространств Н0 = Н0,0, Н1=Н0,1  Н1,0, Н2=Н1,1 и двумерных, инвариантных относительно А, подпространств Нφк φк
Н1,0, Н2=Н1,1 и двумерных, инвариантных относительно А, подпространств Нφк φк  (0,
(0,  ), (к = 1,…, s). При этом операторы Р1 и Р2 неприводимы в Нφк (к = 1,…, s), и собственные значения 1+εк, 1-εк входят одновременно в спектр А. Так как А*=А, то соответствующие собственные векторы ортогональны. Тогда имеет место разложение на собственные подпространства
), (к = 1,…, s). При этом операторы Р1 и Р2 неприводимы в Нφк (к = 1,…, s), и собственные значения 1+εк, 1-εк входят одновременно в спектр А. Так как А*=А, то соответствующие собственные векторы ортогональны. Тогда имеет место разложение на собственные подпространства
Нφк = Н1+εк  Н1-εк , причем dimН1+εк =dimН1-εк = 1 (1.3)
Н1-εк , причем dimН1+εк =dimН1-εк = 1 (1.3)
Если φк ≠ φ i, то εк ≠ εi (так как εк = 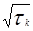 =cosφк и φк
=cosφк и φк  (0,
(0,  )). Объединим все Нφк , у которых одинаковые φк , в одно слагаемое, и обозначим его через Нφк. При этом, если dimНφк = 2qk, то есть Нφк состоит из qk экземпляров двумерных подпространств, отвечающих одному φк , то объединяя вместе все соответствующие одномерные собственные подпространства, получим Нφк = Н1+εк
)). Объединим все Нφк , у которых одинаковые φк , в одно слагаемое, и обозначим его через Нφк. При этом, если dimНφк = 2qk, то есть Нφк состоит из qk экземпляров двумерных подпространств, отвечающих одному φк , то объединяя вместе все соответствующие одномерные собственные подпространства, получим Нφк = Н1+εк  Н1-εк , dimН1+εк =dimН1-εк = qk.
Н1-εк , dimН1+εк =dimН1-εк = qk.
Теорема 1.2. Самосопряженный оператор А представим в виде суммы двух ортопроекторов А = Р1 и Р2 тогда и только тогда, когда
 (А)
(А) 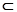 {0, 1, 2}
{0, 1, 2}  (
(  {1+ε , 1-ε}), 0<εк<1,
{1+ε , 1-ε}), 0<εк<1,
причем dimН1+εк =dimН1-εк к = 1,…, m.
Доказательство. Пусть А = Р1 и Р2, тогда его спектр был найден выше:
 (А)
(А) 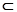 {0, 1, 2}
{0, 1, 2}  (
(  {1+ε , 1-ε}), где 0<εк<1для любого к = 1,…, m.
{1+ε , 1-ε}), где 0<εк<1для любого к = 1,…, m.
Обратно, пусть нам известен спектр оператора А и известно, что размерности соответствующих собственных подпространств совпадают, то есть
dimН1+εк =dimН1-εк . Существует единственное разложение Н в ортогональную сумму инвариантных подпространств ((1.1.) Глава II):
Н = Н(0)  Н(1)
Н(1)  Н(2)
Н(2)  (
(  (С2
(С2  Нк)) (1.4.)
Нк)) (1.4.)
(1.4.) можно записать иначе
Н = Н(0)  Н(1)
Н(1)  Н(2)
Н(2)  (
(  (С2
(С2  (Н1+εк
(Н1+εк  Н1-εк ))) (1.5.)
Н1-εк ))) (1.5.)
Зададим ортопроекторы Р1 и Р2 следующим образом
P1 = P Н 2  (
(  (
( 
 I к )) (1.6.)
I к )) (1.6.)
Р 2 = PН 1 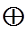 PН 2
PН 2  (
( 

 I к )) (1.7.)
I к )) (1.7.)
где PН к – ортопроектор в Н на Н(к) (к = 1, 2), Is – единичный оператор в Hs s=1,…, m. Но тогда
Р1 + Р2 = PН 1  PН 2
PН 2  (
( 

 Iк )) = А, при этом А = А*
Iк )) = А, при этом А = А*
1.6. Линейная комбинация ортопроекторов. Пусть теперь с. Из (1.2.) следует λ1 + λ2 = a + b. Пусть λ2 = ε, тогда λ1 = a + b – ε.
Оценим ε. Заметим, что (a +b)2 – 4a b(1-τ) = (a - b)2 + 4a bτ > 0.
Тогда ε =  >
>  = 0, то есть ε = 0.
= 0, то есть ε = 0.
Допустим, что ε ≥ a , тогда
a ≤ 
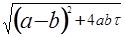 ≤ b – a
≤ b – a
(b - a)2 +4ab τ ≤ (b – a)2
abτ ≤ 0, но abτ > 0 и значит ε < a
Итак,
 λ1 = ε
λ1 = ε
λ2 = a + b – ε. (1.8.)
0 < ε < a
Пусть dimH =n. Тогда справедлива теорема.
Теорема 1.3. Самосопряженный оператор А представим в виде линейной комбинации ортопроекоров А = aР1 + bР2, 0<a<b тогда и только тогда, когда
 (А)
(А) 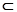 {0, a, b, a + b}
{0, a, b, a + b}  (
(  {εк , a + b - εк}), 0<εк<1, и
{εк , a + b - εк}), 0<εк<1, и
dimНεк =dimНa+ b-εк (Нεк , Нa+ b-εк - собственные подпространства оператора А, отвечающие εк) к=1,…m.
Доказательство. Пусть А = aР1 + bР2, 0<a<b. Найдем 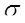 (А).
(А).
1) х  Н0,0, то Ах = 0 и 0
Н0,0, то Ах = 0 и 0 
 (А);
(А);
2) х  Н0,1 , то Ах = bx и b
Н0,1 , то Ах = bx и b 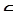
 (А);
(А);
3) х  Н1,0 , то Ах = ax и a
Н1,0 , то Ах = ax и a 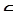
 (А);
(А);
4) х  Н1,1 , то Ах = ( a+ b) x и a+ b
Н1,1 , то Ах = ( a+ b) x и a+ b 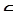
 (А).
(А).
Тогда  (А)
(А) 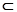 {0, a, b, a + b}
{0, a, b, a + b}  (
(  {εк , a + b - εк}), где 0<εк<1, к=1,…m. Причем числа εк, a + b - εк входят одновременно в спектр А, и соответству-
{εк , a + b - εк}), где 0<εк<1, к=1,…m. Причем числа εк, a + b - εк входят одновременно в спектр А, и соответству-
ющие собственные подпространства ортогональны и одномерны, так как А=А*. Тогда сумма всех собственных подпространств, отвечающих одному εк также инвариантна относительно А и dimНεк =dimНa+ b-εк = qk. (с учетом кратности εк)
Обратно. Существует единственное разложение Н в силу (1.4.)
Н = Н(0)  Н( a)
Н( a) 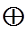 Н( b)
Н( b) 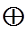 Н( a+ b)
Н( a+ b) 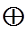 (
(  (С2
(С2  Нк)) (1.9.)
Нк)) (1.9.)
Где Н(0)=Н0,0 , Н( a) =Н1,0 , Н( b)=Н0,1 , Н( a+ b)=Н1,1 или
Н = Н(0)  Н( a)
Н( a)  Н( b)
Н( b)  Н( a+ b)
Н( a+ b)  (
(  (Нεк
(Нεк  Нa+ b-εк) (1.10.)
Нa+ b-εк) (1.10.)
Положим
P1 = Pa  Pa+b
Pa+b  (
(  (
( 
 I к )) (1.11.)
I к )) (1.11.)
Р 2 = Pb  Pa+b
Pa+b  (
( 

 I к )) (1.12.)
I к )) (1.12.)
Но тогда
aР 1 + bР 2 = aPa  bPb
bPb  (а +b)Pa+b
(а +b)Pa+b  (a
(a  (
( 
 I к ))
I к )) 
 (b
(b 
 I к )) = A.
I к )) = A.
Спектр оператора А совпадает с {0, a, b, a + b}  (
(  {εк , a + b - εк}), (0<εк<1, к=1,…m) по построению и А = А* как вещественная комбинация ортопроекторов.
{εк , a + b - εк}), (0<εк<1, к=1,…m) по построению и А = А* как вещественная комбинация ортопроекторов.
|
из
5.00
|
Обсуждение в статье: Спектр ортопроектора в гильбертовом пространстве. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

