УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 

Институт прикладной математики и компьютерных наук

Кафедра информационной безопасности

 

 

Материал для практических занятий по курсу

Теория вероятностей и математическая статистика

 

 

 

Разработчик:

к. т. н., доц. Баранова Е. М.

 

Тула, 2018 г.

Непосредственный подсчет вероятностей

Задача 1

В урне 2 белых и 3 черных шара. Из урны наугад берется 1 шар, найти вероятность того, что этот шар будет черным.

Решение

1. Пусть А – событие, заключающееся в том, что шар будет черным.

2. Поскольку опыт сводится к схеме случаев, вероятность события определяется следующим образом: , где Р(А) – вероятность наступления события А, n – число благоприятствующих событию А случаев, m – общее число случаев.

3. Всего в урне 2+3=5 шаров, т. е. n=5. Событию А благоприятствует 3 случая, т. к. в урне 3 черных шара, т. е. m=3.

4. Определим искомую вероятность: .

Ответ: .

 

Задача 2

В урне 7 белых и 5 черных шаров. Из урны наугад берется 1 шар. Этот шар оказывается белым. Обратно в урну этот шар не кладется. Найти вероятность того, что второй вынимаемый шар также окажется белым.

Решение

1. Пусть А – событие, заключающееся в том, что второй шар окажется белым.

2. Поскольку опыт сводится к схеме случаев, вероятность события определяется следующим образом: , где Р(А) – вероятность наступления события А, n – число благоприятствующих событию А случаев, m – общее число случаев.

3. Всего в урне до наступления опыта было 7+5=12 шаров. После того, как из урны был извлечен первый шар, в урне осталось 12-1=11 шаров, т. е. n=11.

4. Из оставшихся 11 шаров 7-1=6 белых, т. е. m=6.

5. Определим искомую вероятность: .

Ответ: .

Задача 3

Подбрасываются 2 игральных кубика. Найти вероятность того, что сумма выпавших очков на двух кубиках будет равна 8.

Решение

1. Пусть А – событие, заключающееся в том, что сумма выпавших очков равна 8.

2. Поскольку опыт сводится к схеме случаев, вероятность события определяется следующим образом: , где Р(А) – вероятность наступления события А, n – число благоприятствующих событию А случаев, m – общее число случаев.

3. Всего возможно 6*6=36 вариантов сочетания очков на двух кубиках, т. е. n=36.

4.  Благоприятствуют событию А только 5 вариантов:

- на первом кубике 2 очка, на втором 6;

- на первом кубике 6 очков, на втором 2;

- на первом кубике 3 очка, на втором 5;

- на первом кубике 5 очков, на втором 3;

- на первом кубике 4 очка, на втором кубике 4 очка.

Т. е. m=5.

5. Определим искомую вероятность:

Ответ: .

 

Задача 4

В колоде 36 карт. Наугад из колоды вынимаются 5 карт, из них оказывается 2 туза, шестерка, 2 дамы. Найти вероятность того, что следующая вынимаемая из колоды карта окажется

а) десяткой;

б) бубновой десяткой;

в) дамой.

Решение

а)

1. Пусть А – событие, заключающееся в том, что очередная шестая вынимаемая из колоды карта окажется десяткой.

2. Поскольку опыт сводится к схеме случаев, вероятность события определяется следующим образом: , где Р(А) – вероятность наступления события А, n – число благоприятствующих событию А случаев, m – общее число случаев.

3. После пяти опытов в колоде осталось 36-5=31 карта, т. е. n=31.

4. Благоприятствуют событию А 4 варианта, т. к. ни одна из пяти извлеченных из колоды карт не являлась десяткой, т. е. m=4.

5. Определим искомую вероятность: .

б)

1. Пусть В – событие, заключающееся в том, что очередная шестая вынимаемая из колоды карта окажется бубновой десяткой.

2. Поскольку опыт сводится к схеме случаев, вероятность события определяется следующим образом: 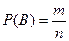, где Р(В) – вероятность наступления события В, n – число благоприятствующих событию В случаев, m – общее число случаев.

3. После пяти опытов в колоде осталось 36-5=31 карта, т. е. n=31.

4. Благоприятствуют событию А только 1 вариант, поскольку в колоде имеется только одна бубновая десятка, причем она среди ранее извлеченных 5 карт не встречалась, т. е. m=1.

5. Определим искомую вероятность: .

в)

1. Пусть С – событие, заключающееся в том, что очередная шестая вынимаемая из колоды карта окажется дамой.

2. Поскольку опыт сводится к схеме случаев, вероятность события определяется следующим образом: , где Р(С) – вероятность наступления события С, n – число благоприятствующих событию С случаев, m – общее число случаев.

3. После пяти опытов в колоде осталось 36-5=31 карта, т. е. n=31.

4. Благоприятствуют событию С 2 варианта, поскольку среди ранее извлеченных 5 карт уже встретилось 2 из имеющихся в колоде четырех дамы, т. е.  m=2.

5. Определим искомую вероятность: .

Ответ:

а) ;

б) ;

с) .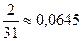

 

 

Комбинаторика

Задача 5

Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, если каждая цифра входит в изображение числа только один раз?

Решение

Записываемые числа будут отличаться только порядком записи цифр, например: 12 345, 12 354, 12 534, 12 543 и т. д., следовательно, необходимо определить возможное количество перестановок .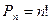

Ответ: 120.

 

Задача 6

Сколько различных вариантов записи имеет следующий набор символов: a b c d? Перечислить варианты записи символов.

Решение

Запись символов будет отличаться только порядком записи их цифр, например: a b c d,    d c b a,    b c a d,  b d a c и т. д., следовательно, необходимо определить возможное количество перестановок 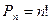. . Варианты записи следующие:

a d c d,  a d b c, a d b c,  a c b d,  a c d b,  a b d c,  d a c d,   b d c a, b d a c, b c a d, b c d a, b a d c, c a b d, c d b a, c d a b, c b a d, c b d a, c a b d, d a b c, d c b a, d c a b, d b a c, d b c a, d a c b.

Ответ: 24.

Задача 7

Сколько можно составить сигналов из 8 флажков различного цвета, взятых по 2?

Решение

Сигналы могут различаться не только порядком расположения цветных флажков, но и составом, например, красный - синий, красный - зеленый, синий - красный, зеленый - красный и т. д. Следовательно, количество сигналов равно числу возможных размещений из 8 по 2: = . Тогда,  или .

Ответ: 56.

 

Задача 8

Сколько можно составить различных, отличающихся либо составом, либо порядком их следования комбинаций из 3 различных фигур, взятых по две? Перечислить эти комбинации. Фигуры имеют вид: ! & *

Решение

Комбинации, различающиеся либо составом, либо порядком называются размещениями. Количество таких комбинаций из 5 по 3 равно: = .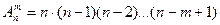

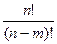Тогда,  или .

Возможные комбинации следующие: ! &, &!, & *, *&, 

! *,    *!

Ответ: 6.

Задача 9

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если каждая цифра входит в изображение числа только один раз? Перечислить эти комбинации.

Решение

Записываемые числа будут отличаться не только порядком записи цифр, но и составом. Такие комбинации называются размещениями: = . Тогда, или .

 

123, 132, 231, 213, 321, 312

234, 243, 324, 342, 432, 423,

345, 354, 453, 435, 534, 543

145, 154, 451, 415, 541, 514

125, 152, 512, 521, 251, 215

124, 142, 241, 214, 421, 412

125, 521, 152, 512, 251, 215

235, 253, 352, 325, 532, 523

341, 314, 413, 431, 134, 143

452, 425, 524, 542, 254, 245

Ответ: 60.

Задача 10

Сколько сочетаний можно составить по данным предыдущей задачи? Перечислить сочетания.

Решение

Количество сочетаний определяется следующим образом: 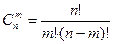. Тогда, .

Этими сочетаниями являются сочетания следующих троек цифр: 1-2-3, 2-3-4, 3-4-5, 4-5-1, 1-2-5, 1-2-4, 1-2-5, 2-3-5, 3-4-1, 4-5-2.

Ответ: 10.

Задача 11

Сколькими способами можно выбрать две детали из ящика, содержащего 10?

Решение

Выбираемые из ящика детали будут отличаться хотя бы одним элементом. Следовательно, число возможных способов равно числу сочетаний: . .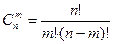

Ответ: 45.

 

 

Задача 12

Сколькими способами можно выбрать 3 детали из ящика, содержащего 5 деталей? Перечислить эти сочетания, если детали имеют следующие сечения: O Δ □ ◊ ⌂.

Решение

Выбираемые из ящика детали будут отличаться хотя бы одним элементом. Следовательно, число возможных способов равно числу сочетаний: . .

Возможными сочетаниями будут: O Δ □,   Δ □ ◊, O Δ ⌂, 

Δ □ ◊,   Δ □ ⌂,   □ ◊ ⌂,   O □ ◊,   Δ □ ◊,   O Δ ⌂,   O Δ ⌂.

Ответ: 10.

Определение вероятности

с элементами комбинаторики

Задача 13

Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Решение

1. Пусть событие А – абонент набрал две нужные цифры.

2.  Всего можно набрать столько двух различных цифр, сколько может быть составлено размещений из десяти цифр по две, т. е. . . Эти исходы несовместимы, равновозможны и образуют полную группу.

3. Событию А благоприятствует только один исход, следовательно, искомая вероятность  .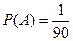

Ответ: .

 

Задача 14

Пациент, придя в поликлинику, забыл номер своей карты, помня лишь то, что в номер карты входили цифры: 2, 3, 4, 5. Найти вероятность того, что пациент в регистратуре со второго раза укажет номер своей карты.

Решение

1. Пусть событие А – пациент со второго раза назвал номер своей карты.

2. Всего можно назвать столько номеров, сколько существует перестановок из цифр 2,3,4,5, т. е. . Тогда . Эти исходы несовместимы, равновозможны и образуют полную группу.

3. По условию задачи предполагается, что пациент в первый раз указал неправильный номер карты. В этом случае у него остается 24-1=23 возможных варианта номера.

4. Событию А благоприятствует только один из оставшихся возможных вариантов, следовательно, искомая вероятность .

Ответ: .

 

Задача 15

В ящике имеется 15 деталей, среди которых 5 окрашенных и 10 бракованных. Сборщик на удачу извлек 3 детали. Найти вероятность того, что эти три извлеченные детали окажутся окрашенными.

Решение

1. Пусть событие А – извлечение трех окрашенных деталей.

2. Общее число исходов, т. е. извлечение из 15 деталей 3 можно определить как число сочетаний: = . = .

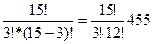3. Число исходов, благоприятствующих событию А можно определить как число сочетаний из 10 по 3. = . = .

4. Тогда, искомая вероятность P ( A )=  = .

Ответ: .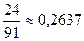

 

Задача 16

В ящике имеется 24 детали, среди которых 9 круглого сечения, остальные – квадратного. Сборщик на удачу извлек 8 деталей. Найти вероятность того, что эти 8 извлеченных деталей окажутся квадратного сечения.

Решение

1.  Пусть событие А – извлечение 8 деталей квадратного сечения.

2. Общее число исходов, т. е. извлечение из 24 деталей 8 можно определить как число сочетаний: = . = .

3. Количество деталей квадратного сечения l =24-9=15.

4. Число исходов, благоприятствующих событию А можно определить как число сочетаний из 15 по 8. = . = .

5. Тогда, искомая вероятность P ( A )= .

Ответ: .

 

Относительная частота

 

Задача 17

Отдел технического контроля обнаружил 6 бракованных деталей в партии из 100 штук. Определить относительную частоту попадания бракованных деталей.

Решение

1. Относительная частота определяется по формуле , где m – число появлений события, n – общее число испытаний.

2. Пусть событие А – попадание бракованных деталей. Искомая относительная частота события А определиться .

Ответ: 0,06.

 

Задача 18

По цели производится 25 выстрелов, причем было зарегистрировано 18 попаданий. Определить относительную частоту поражения цели.  

Решение

1. Относительная частота определяется по формуле , где m – число появлений события, n – общее число испытаний.

2. Пусть событие А –поражение цели. Искомая относительная частота события А определиться .

Ответ: 0,72.

 

Теорема сложения вероятностей

 

Задача 19

В урне 60 шаров: 20 красных, 30 синих, 10 белых. Некто наугад вытаскивает из урны 1 шар. Найти вероятность того, что этот шар будет цветным (синим или красным).

Решение

1. Определим вероятность появления красного шара:

Р_кр= .

2. Определим вероятность появления синего шара:

Р_син= .

3. События «появление красного шара» и «появление синего шара» - несовместимы, поэтому можно применить теорему сложения вероятностей: P (А+В)=Р(А)+Р(В).

Р _цветн=Р_красн+Р_синий

Р _цветн= .

Ответ: .

 

Задача 20

В партии 1000 деталей. Известно, что 100 из них имеют опасные дефекты, 200 – менее опасные дефекты, 300 второстепенные дефекты. Наугад берется одна деталь. Найти вероятность того, что эта деталь будет с опасным или менее опасным дефектом.

Решение

1. Найдем вероятность того, что первая деталь будет с опасным дефектом:

Р_опас = .

2.     Найдем вероятность того, что первая деталь будет с менее опасным дефектом:

Р _{менее опас} = .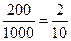

3. События «появление первой детали с опасным дефектом» и «появление первой детали с менее опасным дефектом» - несовместимы, поэтому можно применить теорему сложения вероятностей:

P(А+В)=Р(А)+Р(В)

Р _{опасн+менее опасн}=Р_опасн+Р_{менее опасн}

Р _{опасн+менее опасн}= .

Ответ: .

Задача 21

Стрелок стреляет по мишени, разделенной на две области. Вероятность попадания в первую область . Вероятность попадания во вторую область . Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Решение

1. События «попадание при одном выстреле в первую область» и «попадание при первом выстреле во вторую область» - несовместимы, поэтому можно применить теорему сложения вероятностей:

P(А+В)=Р(А)+Р(В)

Р _1,2=Р₁+Р₂

Р _1,2=0,55+0,35=0,9.

Ответ: .

 

Задача 22

В колоде 36 карт. Наудачу извлекаются 2 карты. Этими картами оказываются дама и туз. Найти вероятность того, что следующая вытянутая из колоды карта окажется либо дамой, либо королем, либо тузом.

Решение

1. После того, как из колоды вытащили 2 карты, в ней осталось 34 карты, причем из них 3 дамы, 4 короля и 3 туза.  

2. Вероятность извлечь даму составит .

3. Вероятность извлечь короля составит .

4. Вероятность извлечь туз составит .

5. Т. к. события А, В, С – несовместимы, можно применить теорему сложения вероятностей: Р(А+В+С)=Р(А)+Р(В)+Р(С).

 

Ответ:

 

Полная группа событий

Задача 23

Консультационный пункт института получает пакеты с контрольными работами из пяти городов. Вероятность получить пакет из города А составляет 0,24, из города В – 0,16, из города С – 0,31, из города D = 0,63. Найти вероятность того, что очередной пакет получен из города Е.  

Решение

1. Пусть А – событие, заключающееся в получении пакета из города А, В – из города В, С – из города С , D – из города D, Е – из города Е. 

5. Т. к. события А, В, С, D , E – составляют полную группу, то сумма их вероятностей равна 1. Тогда, .

Ответ: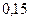

Задача 24

У игрока в руке 3 карты. Вероятность того, что он пойдет левой картой составляет 0,61, правой картой – 0,23. Найти вероятность того, что он пойдет средней картой.

Решение

1. Пусть А – событие, заключающееся в том, что игрок пойдет левой картой, В – правой картой, С – средней картой.  

2. Т. к. события А, В, С – составляют полную группу, то сумма их вероятностей равна 1. Тогда, .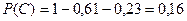

Ответ: