 |
Главная |
Матрицы и действия над матрицами
|
из
5.00
|
Матрицей 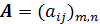 называется прямоугольная таблица чисел, содержащая m строк и n столбцов:[1]
называется прямоугольная таблица чисел, содержащая m строк и n столбцов:[1]
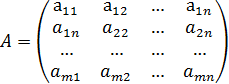 .
.
Числа 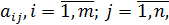 составляющие данную матрицу, называются ее элементами:
составляющие данную матрицу, называются ее элементами:  номер строки матрицы;
номер строки матрицы; 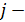 номер столбца.
номер столбца.
Если 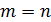 , то матрица называется квадратной порядка
, то матрица называется квадратной порядка 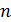 .
.
Квадратная матрица, у которой все элементы, лежащие на главной диагонали, равны единице ( 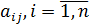 ) а остальные элементы – нулю, называются единичной:
) а остальные элементы – нулю, называются единичной:
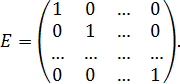
Матрица, состоящая из одной строки, называется вектором-строкой, а матрица, состоящая из одного столбца,  вектором-столбцом.
вектором-столбцом.
Две матрицы 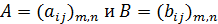 равны, если равны их соответствующие элементы, т.е.
равны, если равны их соответствующие элементы, т.е. 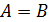 тогда и только тогда, когда
тогда и только тогда, когда 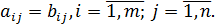
Суммой двух матриц 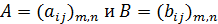 называется матрица
называется матрица 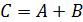 , элементы которой
, элементы которой 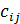 равны сумме соответствующих элементов
равны сумме соответствующих элементов 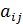 и
и 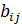 матриц
матриц  и
и  .
.
Произведение матрицы 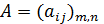 на число
на число 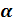 называется матрица
называется матрица 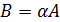 , элементы которой
, элементы которой 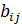 равны
равны
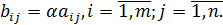
Матрица 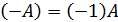 называется противоположной матрице
называется противоположной матрице 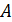 . Если матрицы
. Если матрицы 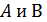 одинаковых размеров, то их разность равна
одинаковых размеров, то их разность равна
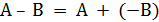 .
.
Произведением матрицы 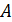 порядка
порядка 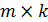 на матрицу
на матрицу 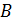 порядка
порядка 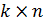 называется матрица
называется матрица 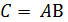 порядка
порядка 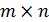 , элементы которой
, элементы которой 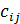 равны
равны
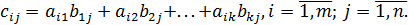
Из данного выражения следует правило умножения матриц: чтобы получить элемент, стоящий на пересечении 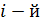 строки и
строки и 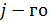 столбца матрицы
столбца матрицы 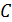 , необходимо все элементы
, необходимо все элементы 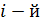 строки матрицы
строки матрицы 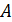 умножить на соответствующие элементы
умножить на соответствующие элементы 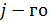 столбца матрицы
столбца матрицы 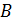 и полученные произведения сложить.
и полученные произведения сложить.
Произведение двух матриц не коммутативно, т.е. в общем случае 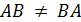 . Если
. Если 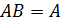 , то матрицы
, то матрицы 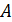 и
и 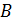 называются коммутативными. Так, единичная матрица
называются коммутативными. Так, единичная матрица 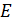 коммутативна с любой квадратной матрицей того же порядка, причем
коммутативна с любой квадратной матрицей того же порядка, причем 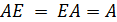 .
.
Пример 1. Найти произведение 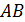 матриц:
матриц:
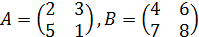 .
.
Решение:
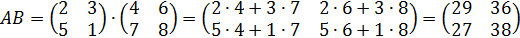 .
.
Пример 2. Найти произведение 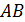 матриц:
матриц:
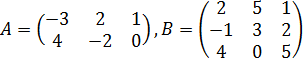 .
.
Решение:
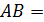
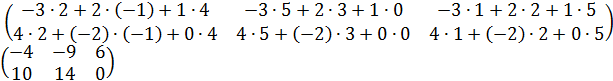 .
.
Транспортированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка (или, что то же самое, замена столбцов матрицы на ее строки). Обозначение транспортированной матрицы: 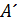 ,
, 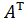 .
.
Любой квадратной матрице 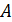 порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем, или детерминантом
порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем, или детерминантом 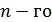 порядка этой матрицы. Начнем с определителей второго и третьего порядков.
порядка этой матрицы. Начнем с определителей второго и третьего порядков.
Пусть дана матрица
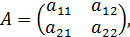
тогда ее определитель второго порядка вычисляется по формуле:
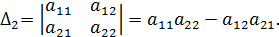
Пример 3. Вычислить определитель матрицы 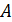 :
:
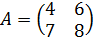 .
.
Решение:
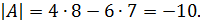
Определитель третьего порядка вычисляется по формуле
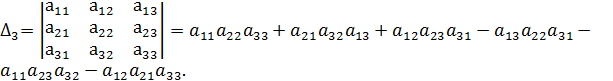
Пример 4. Вычислить определитель матрицы 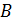 :
:
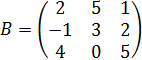 .
.
Решение:
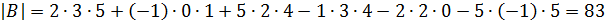 .
.
Вычисление определителей n -го порядка производится на основании свойств определителей и следующей теоремы: определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
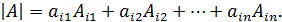
Алгебраическое дополнение 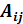 элемента
элемента 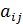 равно
равно
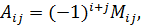
где, 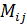 – минор элемента
– минор элемента 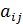 , получаемый путем вычеркивания в определителе
, получаемый путем вычеркивания в определителе 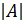
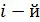 строки и
строки и 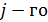 столбца.
столбца.
Минором порядка 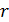 матрицы
матрицы 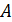 называется определитель
называется определитель 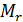 , составленный из элементов, расположенных на пересечении
, составленный из элементов, расположенных на пересечении 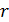 строк и
строк и 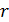 столбцов матрицы. Минор
столбцов матрицы. Минор 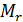 , расположенный в первых
, расположенный в первых 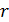 строках и в первых
строках и в первых 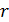 столбцах, называется угловым или главным минором.
столбцах, называется угловым или главным минором.
Пример 5. Вычислить два минора второго порядка матрицы 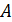 :
:
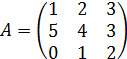 .
.
Решение. Первый минор 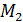 расположен на пересечении первой и третьей строк и второго и третьего столбцов:
расположен на пересечении первой и третьей строк и второго и третьего столбцов:
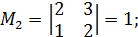
второй минор 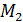 является главным минором второго порядка. Он расположен на пересечении первых двух строк и первых двух столбцов:
является главным минором второго порядка. Он расположен на пересечении первых двух строк и первых двух столбцов:
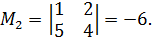
Квадратная матрица 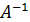 порядка n называется обратной к матрице
порядка n называется обратной к матрице 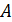 , если она удовлетворяет соотношению:
, если она удовлетворяет соотношению:
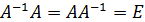 .
.
Квадратная матрица 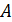 порядка n называется невырожденной (неособенной), если ее определитель отличен от нуля. В противном случае матрица
порядка n называется невырожденной (неособенной), если ее определитель отличен от нуля. В противном случае матрица 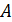 называется вырожденной (особенной).
называется вырожденной (особенной).
Для всякой невырожденной матрицы 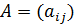 существует единственная обратная матрица, равная
существует единственная обратная матрица, равная
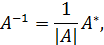
где, 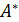
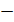 присоединенная матрица,
присоединенная матрица, 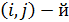 элемент которой есть алгебраическое дополнение
элемент которой есть алгебраическое дополнение 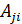 элемента
элемента 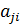 матрицы
матрицы 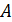 :
:
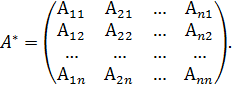
Первый способ нахождения обратной матрицы рассмотрим на конкретном примере:
Пример 6. Вычислить обратную матрицу для матрицы 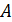 :
:
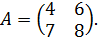
Решение. Определитель матрицы 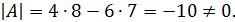
Определитель матрицы 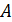 отличен от нуля, следовательно, для матрицы
отличен от нуля, следовательно, для матрицы 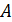 существует единственная обратная матрица. Вычислим присоединенную матрицу
существует единственная обратная матрица. Вычислим присоединенную матрицу 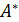 :
:
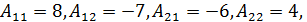
т.е.
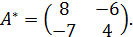
Тогда
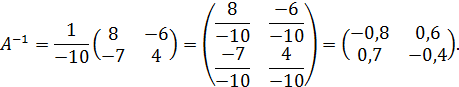
Проверкой убеждаемся, что 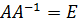 .
.
Второй способ нахождения обратной матрицы. Обратную матрицу можно вычислить на основании следующих элементарных преобразований (преобразований Жордана-Гаусса) над строками матрицы:
· перемена местами двух строк;
· умножение строки матрицы на любое число, отличное от нуля;
· прибавление к одной строке матрицы другой строки, умноженной на любое число, отличное от нуля.
Для того чтобы вычислить обратную матрицу для матрицы 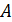 , необходимо составить матрицу
, необходимо составить матрицу 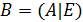 , затем путем элементарных преобразований привести матрицу
, затем путем элементарных преобразований привести матрицу 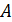 к виду единичной матрицы
к виду единичной матрицы 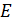 , тогда на месте единичной матрицы получим матрицу
, тогда на месте единичной матрицы получим матрицу 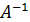 .
.
Пример 7. Вычислить обратную матрицу для матрицы 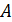 :
:
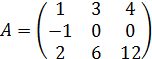 .
.
Решение. Составим матрицу 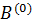 вида
вида
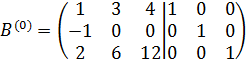 .
.
Элемент 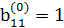 и первую строку, содержащую данный элемент, назовем направляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный столбец с единицей в первой строке. Для этого ко второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и -2. В результате данных преобразований получим матрицу:
и первую строку, содержащую данный элемент, назовем направляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный столбец с единицей в первой строке. Для этого ко второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и -2. В результате данных преобразований получим матрицу:
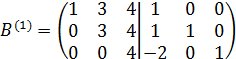 .
.
В матрице 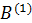 преобразуем в единичный второй столбец. В качестве направляющего элемента выберем элемент
преобразуем в единичный второй столбец. В качестве направляющего элемента выберем элемент 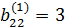 . Так как направляющий элемент
. Так как направляющий элемент 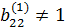 , разделим вторую (направляющую) строку на
, разделим вторую (направляющую) строку на 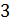 . Затем к первой строке прибавим вторую, умноженную на
. Затем к первой строке прибавим вторую, умноженную на 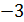 . Получим матрицу
. Получим матрицу
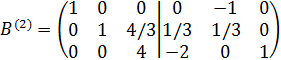 .
.
В матрице 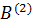 преобразуем в единичный третий столбец. В качестве направляющего элемента выбираем элемент
преобразуем в единичный третий столбец. В качестве направляющего элемента выбираем элемент 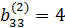 . Делим направляющую (третью) строку на 4 и ко второй строке прибавляем третью, умноженную на
. Делим направляющую (третью) строку на 4 и ко второй строке прибавляем третью, умноженную на 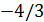 . Получим матрицу:
. Получим матрицу:
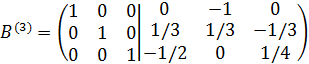 ,
,
откуда
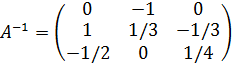 .
.
|
из
5.00
|
Обсуждение в статье: Матрицы и действия над матрицами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

