Коэффициент парной корреляции

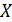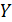Для двух переменных  и  коэффициент парной корреляции определяется следующим образом:

                                      (1)

где,  оценки дисперсий величин 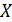 и 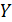. Эти оценки характеризуют степень разброса значений  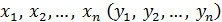вокруг своего среднего соответственно), или вариабельность (изменчивость) этих переменных на множестве наблюдений.

Дисперсия (оценка дисперсии) определяется по формуле

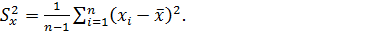(2)

В общем случае для получения несмещенной оценки дисперсии сумму квадратов следует делить на число степеней свободы оценки 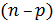, где 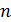 – объем выборки,  – число наложенных на выборку связей. Так как выборка уже использовалась один раз для определения среднего 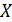, то число наложенных связей в данном случае равно единице 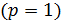, а число степеней свободы оценки (т.е. число независимых элементов выборки) равно .

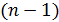Более естественно измерять степень разброса значений переменных в тех же единицах, в которых измеряется и сама переменная. Эту задачу решает показатель, называемый среднеквадратическим отклонением (стандартным отклонением) или стандартной ошибкой переменной 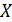 (переменной Y) и определяемый соотношением

                                                   (3)

Если между переменными существует сильная положительная взаимосвязь (увеличение одной переменной при увеличении второй), каждое слагаемое будет положительным числом. Аналогично, если между переменными существует сильная отрицательная взаимосвязь, все слагаемые в числителе будут отрицательными числами, что в результате дает отрицательное значение корреляции.

Знаменатель выражения для коэффициента парной корреляции [см. формулу 1] просто нормирует числитель таким образом, что коэффициент корреляции оказывается легко интерпретируемым числом, не имеющим размерности, и принимает значения от  до .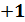

Числитель выражения для коэффициента корреляции, который трудно интерпретировать из-за необычных единиц измерения.

Для качественной оценки коэффициента корреляции применяются различные шкалы, наиболее часто – шкала Чеддока. В зависимости от значения коэффициента корреляции связь может иметь одну из оценок:

0,1 – 0,3 – слабая;

0,3 – 0,5 – заметная;

0,5 – 0,7 – умеренная;

0,7 – 0,9 – высокая;

0,9 – 1,0 – весьма высокая.

Следует отметить, что величина коэффициентов корреляции не является доказательством того, что между исследуемыми признаками существует причинно-следственная связь, а представляет собой оценку степени взаимной согласованности в изменениях признаков. Для того чтобы установить причинно-следственную зависимость, необходим анализ качественной природы явлений.

Так как оценка тесноты связи с помощью коэффициента корреляции проводится, как правило, на основе более или менее ограниченной информации об изучаемом явлении, то возникает вопрос: насколько правомерно наше заключение по выборочным данным о наличии корреляционной связи в той генеральной совокупности, из которой была извлечена выборка?

В связи с этим и возникает необходимость оценки существенности (значимости) линейного коэффициента корреляции, дающая возможность распространить выводы по результатам выборки на генеральную совокупность. В зависимости от объема выборочной совокупности предлагаются различные методы оценки существенности линейного коэффициента корреляции.

Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием t -критерия Стьюдента. При этом фактическое (наблюдаемое) значение этого критерия определяется по формуле:

                                         (4)

Вычисленное по этой формуле значение 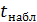 сравнивается с критическим значением t-критерия, которое берется из таблицы значений t-критерия Стьюдента (см. Приложение 2) с учетом заданного уровня значимости и числа степеней свободы .

Если , то полученное значение коэффициента корреляции признается значимым (т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод, что между исследуемыми переменными есть тесная статистическая взаимосвязь.

Если значение  близко к нулю, связь между переменными слабая. Если корреляция между случайными величинами:

· положительная, то при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать;

· отрицательная, при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.

Удобным графическим средством анализа парных данных является диаграмма рассеяния, которая представляется каждое наблюдение в пространстве двух измерений, соответствующих двум факторам.

Диаграмму рассеяния, на которой изображается совокупность значений двух признаков, называют еще корреляционным полем. Каждая точка этой диаграммы имеет координаты . По мере того как возрастает сила линейной связи, точки на графике будут лежать более близко к прямой линии, а величина 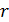 будет ближе к единице.