 |
Главная |
Протокол выполнения регрессионного анализа
|
из
5.00
|
Регрессионная статистика
Дисперсионный анализ
Протокол выполнения регрессионного анализа
Регрессионная статистика |
Дисперсионный анализ | |||||||||||||||
| Множественный R | 0,95 | Df | SS | MS | F | |||||||||||
| R-квадрат | 0,91 | Регрессия | 2 | 39 | 19,5 | 61 | ||||||||||
| Нормированный R-квадрат | 0,89 | Остаток | 13 | 4,1 | 0,32 | |||||||||||
| Стандартная ошибка | 0,56 | Итого | 15 | 43,2 | ||||||||||||
| Наблюдения | 16 | |||||||||||||||
| Коэффициенты | Стандартная ошибка | t- статистика | |
| Y-пересечение | 3,756 | 1,65 | 2,28 |
Браки, 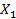
| 0,453 | 0,3 | 1,52 |
Ввод в действие жилых домов в расчете на 1000 чел, кв. м, 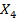
| 0,107 | 0,02 | 4,49 |
Рассмотрим содержание протокола регрессионного анализа (Таблица 9), в котором отражены основные итоги расчетов. Пояснения таблицы «Регрессионная статистика» приведены в табл. 10, а «Дисперсионный анализ» – в табл. 11.
Таблица 10
Регрессионная статистика
| Наименование показателя в отчете Excel | Принятые наименования | Формула |
| Множественный R | Коэффициент множественной корреляции, индекс корреляции | 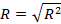
|
| R-квадрат | Коэффициент детерминации 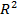
| 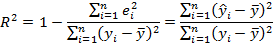
|
| Нормированный R-квадрат | Скорректированный 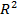
| 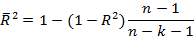
|
| Стандартная ошибка | Среднеквадратическое отклонение от модели | 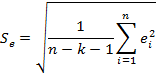
|
| Наблюдения | Количество наблюдений n | n |
Таблица 1
Дисперсионный анализ
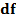 -число степеней свободы -число степеней свободы
| SS -сумма квадратов | MS -среднее значение | F -критерий Фишера | |
| Регрессия | 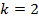
| 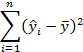
| 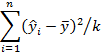
| 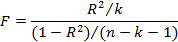
|
| Остаток | 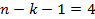
| 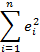
| 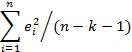
| |
| Итого | 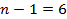
| 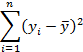
|
В протоколе выполнения регрессионного анализа (таблица 8) отображены коэффициенты уравнения регрессии 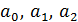 , стандартные ошибки коэффициентов, t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии, индекс корреляции, критерий Фишера и другие параметры.
, стандартные ошибки коэффициентов, t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии, индекс корреляции, критерий Фишера и другие параметры.
Данные матричного исчисления и протокол уравнения регрессии совпали. Зависимость валового регионального продукта от численности работников и основных фондов можно записать в следующем виде:
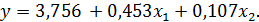
Оценим качество модели.
Значение коэффициентов детерминации и множественной корреляций можно найти в таблице «Регрессионная статистика» (табл. 9).
Коэффициент детерминации:
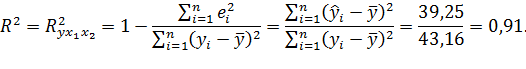
Коэффициент детерминации показывает, что около 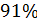 вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
Коэффициент множественной корреляции:
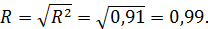
Он показывает высокую тесноту связи зависимой переменной 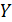 с двумя включенными в модель объясняющими факторами.
с двумя включенными в модель объясняющими факторами.
3. Точность модели оценим с помощью средней ошибки аппроксимации:
| Наблюдение | y | 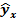
| Остатки
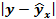
| 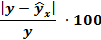
|
| 1 | 8,3 | 8,9 | 0,6 | 7,1 |
| 2 | 8,7 | 8,8 | 0,1 | 0,8 |
| 3 | 9 | 9,2 | 0,2 | 2,3 |
| 4 | 9,7 | 9,5 | 0,2 | 2,5 |
| 5 | 10,2 | 9,9 | 0,3 | 3,1 |
| 6 | 10,4 | 9,9 | 0,5 | 5,0 |
| 7 | 10,2 | 10,4 | 0,2 | 2,0 |
| 8 | 10,4 | 11,1 | 0,7 | 6,5 |
| 9 | 11,3 | 12,4 | 1,1 | 9,6 |
| 10 | 12 | 12,3 | 0,3 | 2,8 |
| 11 | 12,3 | 11,6 | 0,7 | 5,7 |
| 12 | 12,5 | 11,9 | 0,6 | 4,5 |
| 13 | 12,6 | 12,3 | 0,3 | 2,6 |
| 14 | 13,3 | 12,8 | 0,5 | 3,5 |
| 15 | 13,2 | 12,9 | 0,3 | 2,5 |
| 16 | 13,3 | 13,8 | 0,5 | 4,0 |
| Сумма | 64,6 |
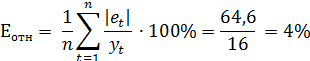
Вывод: 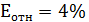 – хороший уровень точности модели.
– хороший уровень точности модели.
4. Использование критерия Дарбина-Уотсона для проверки адекватности выбранного вида уравнения тренда.
При проведении аналитического выравнивания зачастую бывает трудно заранее определить подходящий вид уравнения тренда, особенно если эмпирические данные графически явно не демонстрируют свою приверженность к какой-либо аналитической функции. Тогда поступают следующим образом: строят несколько уравнений тренда, затем для каждого из них вычисляют остаточную дисперсию и модель с наименьшей величиной остаточной дисперсии признают лучшей из имеющихся на данный момент. Но можно пойти и другим путем, а именно: проверить остаточные величины (отклонения фактических значений показателя от выравненных по уравнению тренда) на автокорреляцию. Под автокорреляцией здесь понимается корреляционная зависимость остаточных величин. Если она отсутствует, значит, подобранная модель полностью описывает содержащуюся закономерность в изменении показателя, и, следовательно, адекватно отражает тенденцию в его развитии.
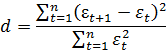
где, 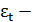 отклонения фактического уровня ряда от его выравненного значения (
отклонения фактического уровня ряда от его выравненного значения ( 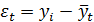 ).
).
Величина 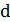 изменяется от 0 до 4. При
изменяется от 0 до 4. При 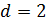 автокорреляция в остаточных величинах отсутствует, следовательно, модель адекватна. При
автокорреляция в остаточных величинах отсутствует, следовательно, модель адекватна. При 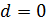 имеется полная положительная, а при
имеется полная положительная, а при 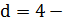 полная отрицательная автокорреляция.
полная отрицательная автокорреляция.
Реально расчетные значения будут находиться между этими границами. Сделать конечный вывод можно с помощью дальнейшей проверки гипотезы об отсутствии автокорреляции в остатках. Для этого расчетное значение 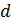 сравнивается с критическими значениями критерия.
сравнивается с критическими значениями критерия.
Таблица 12
Расчетная таблица для вычисления значения критерия
Дарбина-Уотсона
| Условное обозначение времени t | Год | y | 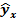
| 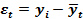
| 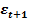
| 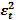
| 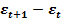
| 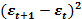
|
| -8 | 1999 | 8,3 | 8,9 | -1 | 0 | 0 | 0 | 0 |
| -7 | 2000 | 8,7 | 8,8 | 0 | 0 | 0 | 0 | 0 |
| -6 | 2001 | 9 | 9,2 | 0 | 0 | 0 | 0 | 0 |
| -5 | 2002 | 9,7 | 9,5 | 0 | 0 | 0 | 0 | 0 |
| -4 | 2003 | 10,2 | 9,9 | 0 | 1 | 0 | 0 | 0 |
| -3 | 2004 | 10,4 | 9,9 | 1 | 0 | 0 | -1 | 0 |
| -2 | 2005 | 10,2 | 10,4 | 0 | -1 | 0 | 0 | 0 |
| -1 | 2006 | 10,4 | 11,1 | -1 | -1 | 0 | 0 | 0 |
| 1 | 2007 | 11,3 | 12,4 | -1 | 0 | 1 | 1 | 1 |
| 2 | 2008 | 12 | 12,3 | 0 | 1 | 0 | 1 | 1 |
| 3 | 2009 | 12,3 | 11,6 | 1 | 1 | 0 | 0 | 0 |
Окончание табл. 12
| 4 | 2010 | 12,5 | 11,9 | 1 | 0 | 0 | 0 | 0 |
| 5 | 2011 | 12,6 | 12,3 | 0 | 1 | 0 | 0 | 0 |
| 6 | 2012 | 13,3 | 12,8 | 1 | 0 | 0 | 0 | 0 |
| 7 | 2013 | 13,2 | 12,9 | 0 | -1 | 0 | -1 | 1 |
| 8 | 2014 | 13,3 | 13,8 | -1 | 0 | 0 | 0 | 0 |
| Сумма | 177,4 | 177,7 | 4,2 | 3,9 |
Тогда расчетное значение критерия равно:
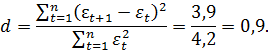
Полученная величина находится в интервале от 0 до 2.
По табл. 13 находим значения критические значения критерия Дарбина-Уотсона.
Таблица 13
Критические значения критерия Дарбина-Уотсона для 0,05 %
Уровня значимости
Количество уровней ряда 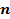
| Нижняя граница 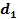
| Верхняя граница 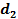
|
| 16 | 1,10 | 1,37 |
Расчетное значение 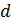 находится в интервале от 0 до 2, то при
находится в интервале от 0 до 2, то при 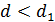 имеется положительная автокорреляция.
имеется положительная автокорреляция.
Положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов. Положительная автокорреляция означает, что отклонения от равновесия имеют тенденцию сохраняться от периода к периоду.
5. Осуществить оценку значимости уравнения регрессии.
Оценим значимость уравнения регрессии. Проверку значимости проведем на основе вычисления F-критерия Фишера:
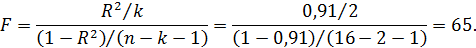
Табличное значение 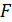 -критерия можно найти с помощью функции F.ОБР.ПХ (2010 Excel). При доверительной вероятности 0,9 при
-критерия можно найти с помощью функции F.ОБР.ПХ (2010 Excel). При доверительной вероятности 0,9 при 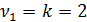 и
и 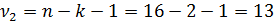 оно составляет 2,67.
оно составляет 2,67.
В нашем примере 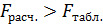 , т.е. 65 > 2,67 уравнение регрессии следует признать адекватным.
, т.е. 65 > 2,67 уравнение регрессии следует признать адекватным.
6. Оценим с помощью t -критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
Анализ статистической значимости параметров модели (коэффициентов регрессии) проводится с использованием t-статистики путем проверки нулю j-го параметра уравнения (кроме свободного члена).
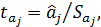
где, 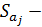 это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии
это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии 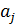 .
.
Величина 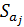 представляет собой квадратный корень из произведения несмещенной оценки дисперсии
представляет собой квадратный корень из произведения несмещенной оценки дисперсии 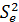 и j-го диагонального элемента матрицы, обратной матрице системы нормальных уравнений:
и j-го диагонального элемента матрицы, обратной матрице системы нормальных уравнений:
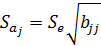
где, 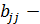 диагональный элемент матрицы
диагональный элемент матрицы 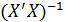 .
.
Значения t-критерия для коэффициентов уравнения регрессии 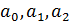 вычислим по формуле 23.
вычислим по формуле 23.
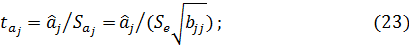
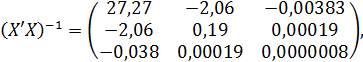
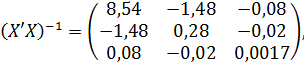
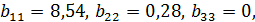 0017,
0017,
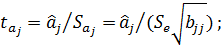
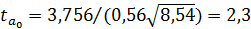 ,
,
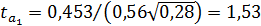 ,
,
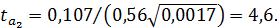
Табличное значение t-критерия Стьюдента можно найти с помощью функции 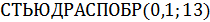 (
( 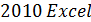 ), при
), при 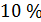 -ом уровне значимости и
-ом уровне значимости и 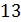 степенях свободы
степенях свободы 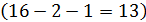 оно составляет
оно составляет 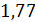 .
.
Так как 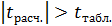 , то коэффициент
, то коэффициент 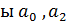 существенны (значимы), коэффициент
существенны (значимы), коэффициент 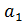 находится рядом с критическим значением, будем считать, что все коэффициенты существенны.
находится рядом с критическим значением, будем считать, что все коэффициенты существенны.
7. Оценить влияние факторов на зависимую переменную по модели.
Для каждого коэффициента регрессии вычислим коэффициент эластичности и бета-коэффициент соответственно по формулам (24) и (25):

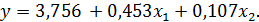
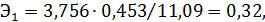
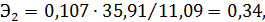

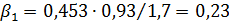 ,
,
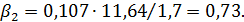
Коэффициент эластичности 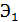 показывает, что при увеличении браков на 1%, рождаемость увеличится на 0,32 тыс. чел., а коэффициент
показывает, что при увеличении браков на 1%, рождаемость увеличится на 0,32 тыс. чел., а коэффициент 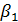 показывает, что при увеличении количества браков на 0,93 (на 1000 человек населения), рождаемость увеличится на 0,4 тыс. чел.
показывает, что при увеличении количества браков на 0,93 (на 1000 человек населения), рождаемость увеличится на 0,4 тыс. чел. 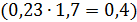 .
.
Коэффициент эластичности 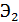 показывает, что при увеличении ввода в действие домов на 1 %, рождаемость увеличится на 0,34 тыс. чел., а коэффициент
показывает, что при увеличении ввода в действие домов на 1 %, рождаемость увеличится на 0,34 тыс. чел., а коэффициент 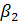 показывает, что при увеличении браков на 11,64 (на 1000 человек населения), количество рождаемость увеличится 1,24 тыс.
показывает, что при увеличении браков на 11,64 (на 1000 человек населения), количество рождаемость увеличится 1,24 тыс. 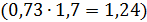 .
.
Долю влияния каждого фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициента 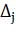 :
:
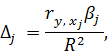
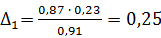 ,
,
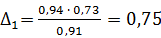 .
.
8. Построить точечный и интервальный прогноз результирующего показателя на два года вперед 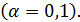
Прогнозируемое значение переменной получается при подстановке в уравнение регрессии ожидаемых значений объясняющих факторов 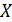 .
.
В нашей задаче необходимо построить прогноз объема реализации на два года вперед. ( 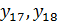 ).
).
Уравнение аппроксимации полиноминального тренда 5-й степени рождаемости в РФ.
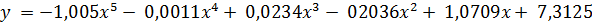 .
.
Надежность уравнения аппроксимации: 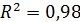 .
.
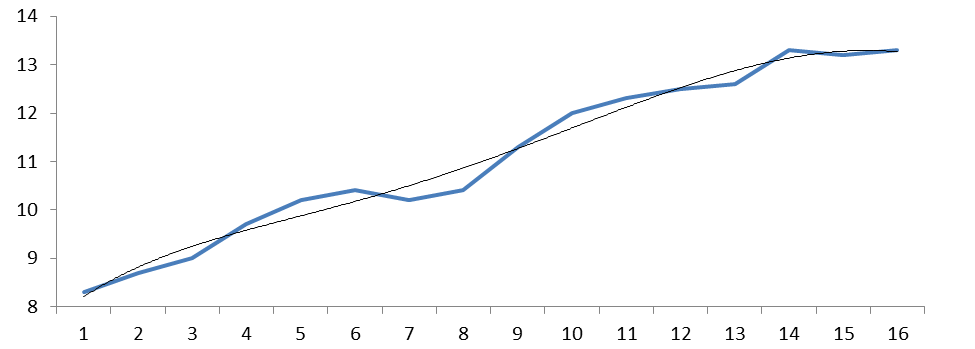
Рис. 2. Динамика рождаемости в РФ 1999-2014 гг., тыс. чел
Для получения прогнозных оценок зависимостей переменной по модели на два года вперед
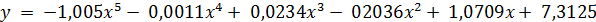 ,
,
подставим в нее найденные прогнозные значения факторов 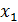 и
и 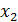 .
.
| Упреждение | Прогноз, тыс. чел |
| 1 | 11,5 |
| 2 | 12,1 |
На рис. 3 приведен результат построение тренда для временного ряда «Ввод в действие жилых домов в расчете на 1000 чел, кв. м».
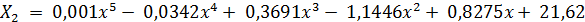 .
.
Надежность уравнения аппроксимации: 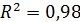 .
.
По которому построен прогноз на два шага вперед:
| Упреждение | Прогноз |
| 1 | 40,1 |
| 2 | 42,5 |
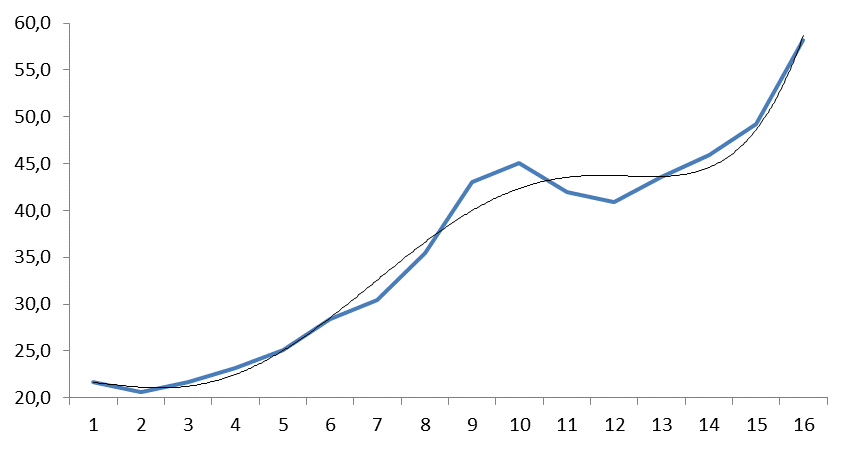
Рис. 3. Динамика ввода в действие жилых домов в расчете
на 1000 чел, кв. м . в РФ 1999-2014 гг., млн. м2
Для получения прогнозных оценок зависимостей переменной по модели
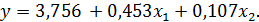
подставим в нее найденные прогнозные значения факторов 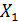 и
и 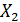 :
:
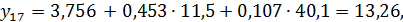
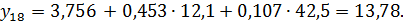
Доверительный интервал прогноза будет иметь следующие границы:
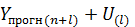 (верхняя граница),
(верхняя граница),
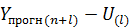 (нижняя граница),
(нижняя граница),
где, 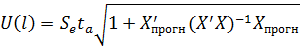 ,
, 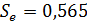 .
.
Распределение Стьюдента при 16-и степенях свободы и 90 % точности:
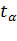
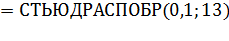 = 1,77.
= 1,77.
На первый шаг ( 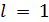 ):
):
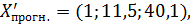
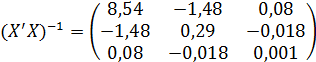
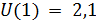 .
.
На второй шаг ( 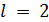 ):
):
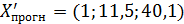 ;
;
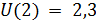 .
.
Результаты прогнозных оценок модели регрессии при 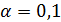 представим в таблице 14.
представим в таблице 14.
Таблица 14
| Упреждение | Прогноз | Нижняя граница | Верхняя граница |
| 1 | 13,3 | 11,2 | 15,4 |
| 2 | 13,8 | 11,5 | 16,1 |
С вероятностью  можно утверждать, что рождаемость (на 1000 человек населения) в следующие два года будет лежать в пределах, указанных в табл. 10.
можно утверждать, что рождаемость (на 1000 человек населения) в следующие два года будет лежать в пределах, указанных в табл. 10.
В наибольшей степени на рождаемость и одновременно на численность населения РФ оказывает влияние такие факторы как браки и ввод в действие жилых домов.
|
из
5.00
|
Обсуждение в статье: Протокол выполнения регрессионного анализа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы