 |
Главная |
Непрерывные математические модели
|
из
5.00
|
Математическая модель системы может быть получена на основе математических моделей подсистем, образующих данную систему.
Математическая модель системы
Рассмотрим в качестве примера непрерывную стационарную одномерную детерминированную систему с сосредоточенными параметрами

Всего три подсистемы: объект  , регулятор
, регулятор  и элемент сравнения
и элемент сравнения  .
.
Объект — динамическая система, дифференциальные уравнения которой могут быть записаны следующим образом:

Х — любая линейная или нелинейная функция.
Составим уравнение регулятора:
Регулятор — также динамическая система, при этом с учётом направленности действия уравнение регулятора не будет содержать х:

Примечание. Направленность действия означает то, что объект не оказывает обратного влияния на регулятор, а только через элемент сравнения и главную обратную связь
Составим уравнение элемента сравнения:

Система уравнений  ,
,  ,
,  — это математическая модель рассматриваемой системы.
— это математическая модель рассматриваемой системы.
В общем случае это система нелинейных дифференциальных уравнений.
Линеаризация математической модели
Если нелинейности системы несущественны, то ими пренебрегают, и считают модель линейной с какой-то степенью приближения.
Линейные модели используют обычно на этапе предварительного проектирования, они удобны для исследования.
Применяя соответствующий метод линеаризации, можно перейти от линейной модели к линеаризованной.
Рассмотрим один из этих методов:
он опирается на гипотезу малости отклонений “Δ”-вариаций переменных х( t ), y ( t ), r ( t ), f ( t ),  от их значений, от их заданных или фиксированных значений “0” х0( t ), y 0 ( t ), r 0 ( t ), f 0 ( t ),
от их значений, от их заданных или фиксированных значений “0” х0( t ), y 0 ( t ), r 0 ( t ), f 0 ( t ), 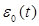 , например, в установившемся состоянии.
, например, в установившемся состоянии.
Рассмотрим уравнение объекта  :
:
Полагая  и
и  , решения уравнения
, решения уравнения  можно найти в виде
можно найти в виде  , а уравнения
, а уравнения  в виде
в виде  , тогда:
, тогда:


Лекция №6. 26.02.2003
Если X непрерывная и однозначная функция, то её можно разложить в ряд Тейлора в окрестности некоторых точек х0 , r 0 , f 0 :




 .
.
Пренебрегая членами ряда порядка выше первого (из-за их малости), с учётом частного случая (в установившемся состоянии после переходного режима при  ,
,  ) после преобразований в операторной форме это уравнение (
) после преобразований в операторной форме это уравнение (  ) можно записать в следующем виде:
) можно записать в следующем виде:

Здесь  , а DO, MO, NO —полиномы от оператора р такие, что:
, а DO, MO, NO —полиномы от оператора р такие, что:
 ;
;
 ;
;
 , где:
, где:
 ;
;
 ;
;
 .
.
Аналогично могут быть получены линеаризованные уравнения регулятора и устройства сравнения:


Исключая из системы уравнений  ,
,  ,
,  переменные
переменные  ,
,  и опуская индекс вариации Δ, линеаризованная математическая модель системы примет вид:
и опуская индекс вариации Δ, линеаризованная математическая модель системы примет вид:
 (II΄)
(II΄)
где:
 ;
;
 ;
;
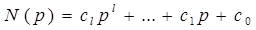 ,
,
где a 0 – an, b 0 – bn, c 0 – cn однозначно определяются коэффициентами α, β и γ системы.
Тот же вид, но в развёрнутой форме:

 (II)
(II)
|
из
5.00
|
Обсуждение в статье: Непрерывные математические модели |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

