 |
Главная |
Необходимые и достаточные условия устойчивости линейных стационарных систем
|
из
5.00
|
Пусть известна математическая модель системы, описывающая свободное движение системы в виде однородного дифференциального уравнения:
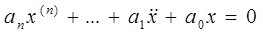 (1)
(1)
или разностного уравнения
 (1΄)
(1΄)
и пусть x — это отклонение интересующей нас переменной от её значения в равновесном режиме. Тогда система будет устойчива, если выполняется условие  (2)
(2)
или  (2΄)
(2΄)
При каких условиях выполняется равенство (2)?
Уравнениям (1) и (1΄) соответствуют характеристические уравнения:
 … (3)
… (3)
 … (3΄)
… (3΄)
Если корни si уравнения (3) различны, то решение уравнения (1) может быть записано следующим образом  .
.
В общем случае корни являются комплексными si =α i + j β i.

1) Если α k >0 A →∞ 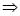 система не устойчива.
система не устойчива.
2) Если α k <0 A →0 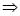 система устойчива.
система устойчива.
3) Если α k =0 A = ck = const 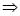 система нейтрально устойчива.
система нейтрально устойчива.
Следовательно, для устойчивости линейной непрерывной стационарной системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, то есть располагались в левой полуплоскости плоскости S.
Можно показать, что для устойчивости дискретной линейной стационарной системы необходимо и достаточно, чтобы все корни характеристического уравнения (3΄) zi были: | zi |<1 … (!!)
Лекция №8. 05.03.2003
Решение уравнения состояния
 (5)
(5)
Пусть при t = t 0 X ( t 0 )= X 0 (начальные условия). Из теории дифференциальных уравнений известно, что решение уравнения (5) при известных начальных условиях может быть получено в следующем виде:
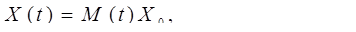 (6)
(6)
где M ( t ) — фундаментальная или переходная матрица.
Решение уравнения (5) можно записать и в виде ряда Тейлора:
 (7)
(7)
Производные в формуле (7) можно определить из уравнения (5):


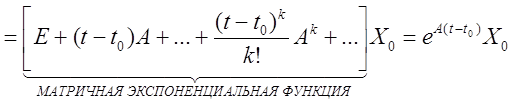
т.е.  (8)
(8)
Здесь  (9)
(9)
е At — МАТРИЦИАНТ.
Можно сказать, что решение неоднородного уравнения состояния  имеет вид:
имеет вид:
 (10)
(10)
Дискретные математические модели многомерной системы
Рассмотрим многомерный импульсный фильтр:

1 — непрерывная часть системы;
4 — формирователи.
В случае экстраполятора нулевого порядка (Э0П) управляющие сигналы yp ( t ), действующие на непрерывную часть системы, будут кусочно-постоянными, т.е. yp ( t )= yp [ iT ], iT ≤ t ≤ ( i +1) T в скалярной форме или Y ( t )= Y [ iT ] при iT ≤ t ≤ ( i +1) T в векторной.
Рассмотрим уравнение (10) при следующих условиях:
1) t 0 = iT — начальные условия.
2) ( iT , t ) — интервал интегрирования.



В частности, при t =( i +1) T:

Таким образом:
 (11)
(11)
Это уравнение состояния многомерной дискретной системы.
Здесь:
 (12)
(12)
е AT — МАТРИЦИАНТ.
 (13)
(13)  (14)
(14)
В развёрнутой форме уравнение состояния примет вид:
 (III)
(III)
Пример 4.
Определить уравнение состояния многомерной импульсной системы с Э0П. Математическая модель непрерывной части известна:

1. Составим уравнение состояния непрерывной части системы:
 ,
,  , тогда
, тогда 

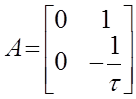

2.

3.








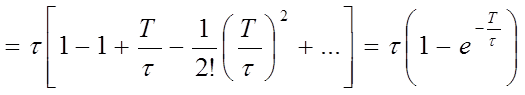
4.


5.

6. Запишем уравнение состояния:
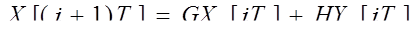

 (III΄)
(III΄)
Лекция №9. 11.03.2003
|
из
5.00
|
Обсуждение в статье: Необходимые и достаточные условия устойчивости линейных стационарных систем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

