Способы задания поверхности на чертеже

а). Аналитический способ – поверхность рассматривают как множество точек, координаты которых удовлетворяют заданному уравнению, т.е. поверхность задается уравнением.

б). Каркасный способ –поверхность задается множеством принадлежащих линий, которое называется каркасом (рис. 4.2.1). Каркас может быть непрерывным, если множество линий сплошь заполняют данную поверхность, и дискретный – совокупность отдельных линий данной поверхности, например – поверхность обшивки самолета, корпуса судна, кузова автомобиля, рельеф земной поверхности (рис. 4.2.2).

                 Рис. 4.2.1                 Рис. 4.2.2

в). Кинематический – поверхность рассматривается как совокупность всех положений движущейся линии и задается определителем.

Определитель – это совокупность геометрических элементов, определяющих поверхность. Он состоит из геометрической (перечень геометрических фигур, образующих поверхность) и алгоритмической (закон перемещения образующих) частей. Общий вид определителя можно записать так Φ (Г) [A], где Г – геометрическая часть, А – алгоритмическая часть. Например: Θ (l ∩ b) – плоскость, заданная пересекающимися прямыми, так как плоскость – это элементарная поверхность алгоритмическая часть определителя отсутствует. Помимо этого поверхность на чертеже задается очерком. Очерк это линия пересечения плоскости проекций с проецирующей поверхностью, которая огибает заданную (рис. 4.2.3).

Рис. 4.2.3

Линия контура делит поверхность на видимую и невидимую части. Видима на плоскости проекций та часть поверхности, которая расположена между наблюдателем и линией контура, та часть поверхности, которая расположена за линией контура – невидима. На плоскостиП₂ точка В видима, а точка А невидима, а на плоскости П₁ наоборот.

Условная классификация поверхностей

Поверхности по их определенным признакам могут быть разбиты на ряд отдельных классов, причем это деление условное, так как одна и та же поверхность может быть отнесена к двум и более классам.

1. По форме образующей поверхности: поверхности линейчатые, которые образуются движением прямолинейной образующей и нелинейчатые, которые образуются движением криволинейной образующей.

2. По закону движения образующей поверхности: поверхности вращения, поверхности с поступательным перемещением образующей, винтовые поверхности.

3. По признаку развертываемости: развертываемые, которые можно совместить с плоскостью проекций без складок и разрывов и неразвертываемые, не совмещающиеся с плоскостью без складок и разрывов.

4. По закону образования: закономерные, если известен закон ее образования и незакономерные, если закон образования неизвестен.

5. Поверхности с постоянной образующей, образующая которых не изменяет своей формы в процессе образования поверхности и поверхности с переменной образующей, образующая которых изменяет свою форму в процессе образования поверхности.

Линейчатые развертывающиеся поверхности

Гранные поверхности

Гранные поверхности образуются перемещением прямолинейной образующей по ломаной направляющей.

Гранные поверхности делятся на пирамидальные и призматические.

Пирамидальные образуются перемещением прямолинейной направляющей по ломаной образующей, причем все образующие имеют одну общую неподвижную точку, которая называется вершиной пирамидальной поверхности (рис. 4.4.1.1). Определитель поверхности: Φ_{п (}l,m, S) [l ∩ m, S∈l].

Если вершина перемещена в несобственную точку, то образуется призматическая поверхность, у которой все ребра параллельны друг другу. Призматическая поверхность образуется перемещением прямолинейной образующей по ломаной направляющей, причем се образующие перемещаются параллельно некоторому заданному направлению (рис. 4.4.1.2). Определитель:Φ_пр (l, m, S) [l ∩ m, l // S].

Поверхности называются открытыми, если направляющая незамкнута. В противном случае поверхности открытые (рис. 4.4.1.1, 4.4.1.2).

                 Рис. 4.4.1.1                     Рис. 4.4.1.2

Если направляющая замкнется, то образуются призма и пирамида. Пирамида – многогранник, в основании которого лежит многоугольник (правильный или неправильный, а боковые грани – треугольники, имеющие общую точку. Призма – многогранник, в основании которого лежат многоугольники, а боковые грани являются прямоугольниками.

Точка принадлежит поверхностям, если она принадлежит образующей (рис. 4.4.1.1, 4.4.1.2, 4.4.1.3 а) или линии параллельной основанию (рис. 4.4.3 б), принадлежащим поверхностям.

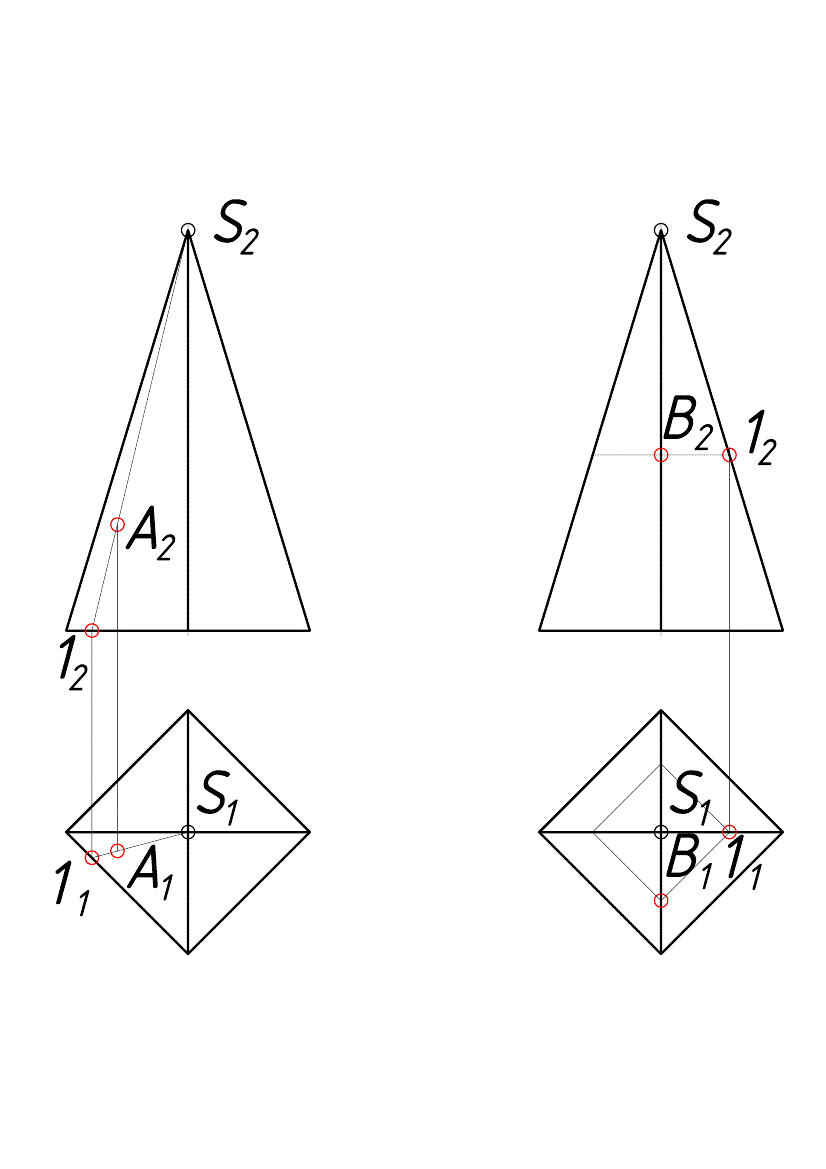
                                 а)                                                     б)

Рис. 4.4.1.3

На рис. 4.4.1.4 показано построение линии, принадлежащей боковой поверхности призмы.

Рис. 4.4.1.4

Торсовые поверхности

Торсовые поверхности относятся к линейчатым развертывающим поверхностям. Они образуются перемещением прямолинейной образующей по криволинейной направляющей. Они делятся на конические, цилиндрические и торсы.

Коническая поверхность образуется движением прямолинейной образующей по криволинейной направляющей, причем все образующие имеют неподвижную общую точку, которая называется вершиной конической поверхности (рис. 4.4.2.1). Точка принадлежит конической поверхности, если она принадлежит образующей, лежащей на этой поверхности (рис. 4.4.2.1, 4.4.2.2).

                  Рис. 4.4.2.1                                                   Рис. 4.4.2.2

На рис. 4.4.2.2 показаны ортогональные проекции конической поверхности. Определитель поверхности Φ_к (l, m, S) [l ∩ m, S∈l].

Цилиндрическая поверхность образуется перемещением прямолинейной образующей по криволинейной направляющей, причем все образующие перемещаются параллельно заданному направлению (рис. 4.4.2.3). Точка принадлежит цилиндрической поверхности, если принадлежит образующей лежащей на этой поверхности (рис.4.4.2.3, 4.4.2.4).

              Рис. 4.4.2.3                                                           Рис. 4.4.2.4

 На рис. 4.4.2.4 показаны ортогональные проекции цилиндрической поверхности. Определитель поверхности: Φ_ц (l, m, S) [l ∩ m, l//S].

На рисунках показаны открытые поверхности. Если направляющая замкнется, то образуются конус и цилиндр, которые иначе называют поверхностями вращения.

Торс – поверхность, образованная движением прямолинейной образующей, которая во всех своих направлениях является касательной к некоторой пространственной кривой, называемой ребром возврата (рис. 4.4.2.5).

Рис. 4.4.2.5