 |
Главная |
Структурное представление моделей
|
из
5.00
|
Представление математических моделей систем в виде структурных схем, описываемых в терминах передаточных функций, является традиционным подходом, применяемым при исследовании и проектировании систем управления. Используя понятие стохастического матричного оператора, можно распространить такой подход на стохастические системы управления, обеспечив наглядную форму представления проекционной модели. Рассмотрим метод анализа систем управления со случайными параметрами, основанный на использовании стохастических матричных операторов и структурного представления проекционной модели системы.
Этот метод особенно удобен для построения проекционных моделей сложных систем управления. В качестве исходного описания системы используются модели ее отдельных элементов в виде дифференциальных уравнений n -го порядка со случайными коэффициентами. Последовательность действий при построении модели системы следующая:
1. Определяются выражения для спектральных характеристик (СХ) всех элементов системы и строится структурная схема системы в спектральной области. Такая схема внешне отличается от обычной структурной схемы только тем, что вместо передаточных функций ее элементов используются выражения для их СХ.
Выражения для СХ отдельных элементов определяются стандартными методами проекционной аппроксимации их моделей (заданных в виде линейных дифференциальных уравнений, в том числе со случайными коэффициентами) с использованием матричных операторов интегрирования и умножения [66] и представляют собой матричные формулы. В качестве ортогонального базиса используются функции Уолша. Выражения для СХ элементов, имеющих случайные параметры, содержат случайные коэффициенты в виде случайных чисел или случайных матриц операторов умножения.
2. Определяется выражение для СХ всей системы, которое получается как результат преобразования («свертывания») полученной на предыдущем этапе структурной схемы, построенной по проекционным моделям (спектральным характеристикам) отдельных элементов, охваченных прямыми и обратными связями.
Используемые при этом правила структурных преобразований во многом похожи на те же правила для передаточных функций с учетом специфики нестационарных систем. Если структурная схема содержит перекрестные связи, то СХ системы может быть получена путем записи выражений для СХ выходных сигналов всех ее отдельных элементов и последовательного исключения переменных (векторов СХ выходных сигналов элементов схемы) из этих выражений. В результате получается выражение, связывающее только СХ входа и выхода.
3. Выражение для СХ всей системы, полученное на предыдущем этапе, содержит обратные матрицы вида , где
-случайная матрица. Чтобы избежать проблемы осреднения обратной матрицы применяется описанный выше прием разложения обратной матрицы в матричный ряд, с предварительным представлением матрицы
в виде
где
-ее математическое ожидание;
-случайная составляющая:
(формула 1.192)
где
Матрица представляет собой матричный оператор умножения на случайную функцию времени, соответствующую случайному параметру одного из элементов структурной схемы. Если этот параметр является случайной величиной асл, то A сл = асл • I, где I — единичная матрица. Если же он является случайной функцией времени, то применяется следующее разложение, представляющее собой спектральный аналог канонического разложения случайной функции:
(формула 1.193)
где - гауссовы случайные величины с единичной дисперсией и нулевым средним значением;
-матрицы операторов умножения на неслучайные координатные функции
.
Таким образом, выше изложена процедура преобразования исходного выражения для СХ всей системы, полученного на втором этапе, к виду, удобному для дальнейших вычислений, т. е. это выражение теперь не содержит случайных матриц и представляет собой сумму произведений неслучайных матриц на случайные числа и в таком виде легко поддается осреднению.
Анализ систем, параметры которых являются
случайными величинами
Зависимость между спектральными характеристиками входа и выхода системы, описываемой моделью (1.178), имеет вид
(формула 1.194)
где стохастический матричный оператор определяется выражением (1.179).
Определим математическое ожидание выходного сигнала системы. Осреднив (1.194) по множеству реализаций, получим соотношение
(формула 1.195)
согласно которому спектральная характеристика математического ожидания выходного сигнала определяется как линейное преобразование спектральной характеристики математического ожидания входного сигнала
детерминированным матричным оператором
, который представляет собой математическое ожидание случайной матрицы стохастического матричного оператора A.
Определим матричный оператор как
(формула 1.196)
Вводя обозначение
(формула 1.197)
запишем выражение для v -го приближения матричного оператора Аср
(формула 1.198)
при этом нулевое приближение определяется следующим образом:
(формула 1.199)
выражения для моментов (1.197) могут быть раскрыты для каждого V например
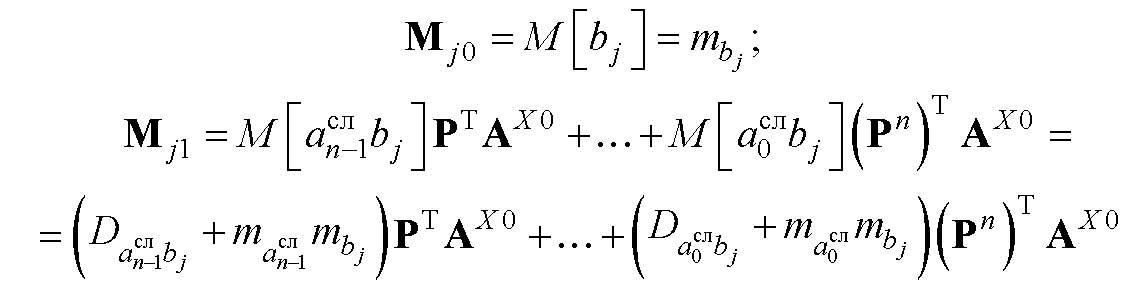
где буквами m и D с индексами обозначены соответственно математические ожидания и взаимные корреляционные моменты соответствующих индексов.
Стохастические моменты выше второго порядка, например появляющиеся в выражении для M .2 моменты третьего порядка, для нормально распределенных ai, b. можно разложить на моменты первого и второго порядка, пользуясь известными соотношениями [97].
На практике редко приходится учитывать статистическую связь между случайными коэффициентами исходного дифференциального уравнения (1.178), поэтому вместо совместных моментов для коэффициентов ai и b . можно с целью упрощения рассматривать произведения их моментов. При этом для нормально распределенных коэффициентов достаточно выражать эти моменты через моменты первого и второго порядков, т.е. через математические ожидания и дисперсии. Если закон распределения случайных коэффициентов отличен от нормального, то задания первых двух моментов уже недостаточно — здесь целесообразно использовать другие числовые характеристики вероятностных распределений, к которым относятся кумулянты [73]. Это позволяет ограничиться конечным числом кумулянтов, поскольку в отличие от моментов, значимость которых с ростом их порядка не убывает, кумулянты обладают свойством уменьшения значимости с увеличением порядка. Для нормального (гауссова) закона распределения вероятности все кумулянты выше второго порядка равны нулю. При этом кумулянт первого порядка равен первому начальному моменту — математическому ожиданию, а кумулянт второго порядка равен второму центральному моменту — дисперсии.
Связь между начальными моментами и коммулянтами порядка r скалярной случайной величины определяеться следующим тождеством
(формула 1.200)
Разлагая экспоненту в правой части (1.200) в ряд получим
перемножая члены этого ряда и сравнивая члены полученного в результате ряда с членами при тех же степенях ряда в левой части (1.200), можно получить формулы, связывающие начальные моменты и кумулянты. Например, для начального момента четвертого порядка имеем
Для нормально распределенной случайной величины ее стохастические моменты порядка r всегда могут быть выражены через моменты первого и второго порядков согласно соотношению
(формула 1.201)
из которого, сравнивая члены при одинаковых степенях в его правой и левой части, можно получить соответствующие формулы.
Например,
где ma, Da — соответственно математическое ожидание и дисперсия случайной величины a. Таким образом, математическое ожидание выходного сигнала системы
может быть вычислено с требуемой точностью, определяемой номером используемого приближения матричного оператора Аср и числом удерживаемых членов разложения по ортогональному базису p.
Для определения корреляционной функции выходного сигнала воспользуемся соотношением
(формула 1.202)
где спектральная характеристика второго начального момента определяется так:
|
из
5.00
|
Обсуждение в статье: Структурное представление моделей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

