 |
Главная |
Методы анализа основной тенденции (тренда) в рядах динамики
|
из
5.00
|
После того как установлено наличие тенденции в ряду динамики, производится ее описание с помощью методов сглаживания. Методы сглаживания разделяются на две основные группы:
1) сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней;
2) выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний.
Рассмотрим каждый из них.
Метод усреднения по левой и правой половине. Разделяют ряд динамики на две части, находят для каждой из них среднее арифметическое значение и проводят через полученные точки линию тренда на графике.
Метод укрупнения интервалов. Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдаются снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. Поэтому для наглядного представления тренда применяется метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т. д.
Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т. д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название – скользящая средняя.
Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода.
Для каждого конкретного ряда динамики (y1, y2, ..., yn) алгоритм расчета скользящей средней следующий.
Определить интервал сглаживания, т. е. число входящих в него уровней m (m < n), используя правило: если необходимо сгладить мелкие, беспорядочные колебания, то интервал сглаживания берут по возможности большим, и, наоборот, интервал сглаживания уменьшают, когда нужно сохранить более мелкие волны и освободиться от периодически повторяющихся колебаний, возникающих, например, из-за автокорреляций уровней.
Вычислить среднее значение уровней, образующих интервал сглаживания, которое одновременно является сглаживающим значением уровня, находящегося в центре интервала сглаживания, при условии, что m – нечетное число, по одной из формул:
 или или 
| (10.22) |
где уi – фактическое значение i-го уровня; m – число уровней, входящих в интервал сглаживания (m = 2р + 1); уt – текущий уровень ряда динамики; i – порядковый номер уровня в интервале сглаживания; р – при нечетном m равно: р = (m – 1) / 2.
Определение скользящей средней по четному числу членов ряда динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания.
Если число членов скользящей средней обозначить через 2m, то серединным будет уровень, относящийся m + 1/2 члену ряда, т. е. имеет место сдвиг периода, к которому относится уровень. Например, средняя, найденная для четырех членов, относится к середине между вторым и третьим периодами, следующая средняя – к середине между третьим и четвертым, и т. д. Чтобы ликвидировать такой сдвиг, применяют так называемый способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. При центрировании необходимо находить скользящие суммы, скользящие средние нецентрированные по этим суммам и средние из двух смежных нецентрированных скользящих средних.
Сдвинуть интервал сглаживания на одну точку вправо, потом вычислить по формуле (10.22) сглаженное значение для t + 1 члена, снова произвести сдвиг и т. д. В результате последовательного применения приведенной итеративной процедуры получится n – (m – 1) новых сглаженных уровней.
Первые и последние р членов ряда с помощью данного алгоритма сгладить нельзя, так как их значения теряются.
Покажем расчет 5-летней и 4-летней скользящих средних на примере данных табл. 10.7.
Метод простой скользящей средней вполне приемлем, если графическое изображение ряда динамики напоминает прямую линию. В этом случае не искажается динамика исследуемого явления. Однако когда тренд выравниваемого ряда имеет изгибы и к тому же желательно сохранить мелкие волны, использовать для сглаживания ряда метод простой скользящей средней нецелесообразно, так как простая скользящая средняя может привести к значительным искажениям исследуемого процесса. В таких случаях более надежным является использование взвешенной скользящей средней.
Метод взвешенной скользящей средней. Взвешенная скользящая средняя отличается от простой скользящей средней тем, что уровни, входящие в интервал усреднения, суммируются с различными весами. Это связано с тем, что аппроксимация сглаживаемого ряда динамики в пределах интервала сглаживания осуществляется с использованием уровней, рассчитанных по полиному 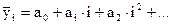 (здесь i – порядковый номер уровня в интервале сглаживания). Полином первого порядка
(здесь i – порядковый номер уровня в интервале сглаживания). Полином первого порядка  есть уравнение прямой, следовательно, метод простой скользящей средней является частным случаем метода взвешенной скользящей средней. Коэффициенты полиномов находятся по способу наименьших квадратов.
есть уравнение прямой, следовательно, метод простой скользящей средней является частным случаем метода взвешенной скользящей средней. Коэффициенты полиномов находятся по способу наименьших квадратов.
Таблица 10.7
Сглаживание урожайности зерновых культур в хозяйстве за1992 – 2007 гг. методом скользящей средней
| Год | Цент- неров с 1 га | Сколь- зящие пяти- летние суммы | Пяти- летние сколь- зящие средние | Сколь- зящие четы- рехлет- ние суммы | Четы- рехлет- ние скользя- щие средние (нецент- риро- ванные) | Четы- рехлет- ние скользя- щие средние (цент- риро- ванные) | Взве- шенные пятилет- ние скользя- щие средние |
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1992 | 9,5 | ― | ― | ― | ― | ― | ― |
| 1993 | 13,7 | ― | ― | ― | 12,3 | ― | ― |
| 1994 | 12,1 | ― | 12,5 | ― | 13,2 | 12,8 | 12,8 |
| 1995 | 14,0 | ― | 13,7 | 49,3 | 13,7 | 13,5 | 13,4 |
| 1996 | 13,2 | 63,5 | 14,1 | 53,0 | 14,6 | 14,1 | 14,3 |
| 1997 | 15,6 | 68,6 | 14,4 | 54,9 | 14,6 | 14,6 | 14,7 |
| 1998 | 15,4 | 70,3 | 15,2 | 58,2 | 15,7 | 15,1 | 15,1 |
| 1999 | 14,0 | 72,2 | 15,6 | 58,2 | 15,6 | 15,6 | 15,4 |
| 2000 | 17,6 | 75,8 | 14,7 | 62,6 | 14,5 | 15,0 | 15,6 |
| 2001 | 15,4 | 78,0 | 15,1 | 62,4 | 15,3 | 14,9 | 14,9 |
| 2002 | 10,9 | 73,5 | 15,3 | 57,9 | 14,7 | 15,0 | 14,3 |
| 2003 | 17,5 | 75,4 | 15,5 | 61,4 | 15,5 | 15,1 | 15,2 |
| 2004 | 15,0 | 76,4 | 15,2 | 58,8 | 16,3 | 15,8 | 16,2 |
| 2005 | 18,5 | 77,3 | 16,0 | 61,9 | 15,65 | 15,97 | 16,3 |
| 2006 | 14,2 | 76,1 | ― | 65,2 | ― | ― | ― |
| 2007 | 14,9 | 80,1 | ― | 62,6 | ― | ― | ― |
На первом этапе сглаживания определяются интервал сглаживания и порядок аппроксимирующего полинома – параболы. Считается, что при использовании полиномов высоких степеней и при меньших размерах интервалов сглаживание ряда динамики будет более «гибким».
Центральная ордината параболы принимается за сглаженное значение соответствующего фактическим данным уровня. Поскольку отсчет времени в пределах интервала, сглаживания производится от его середины, т. е. (t = 1) i =..., -2, -1, 0, 1, 2, ..., то сглаженное значение уровня равно параметру а0 подобранной параболы и является соответствующей скользящей средней. Поэтому для сглаживания нет необходимости прибегать к процедуре подбора системы парабол, так как величину а0 можно получить как взвешенную среднюю из m уровней.
Например, если в интервал сглаживания входят пять последовательных уровней ряда со сдвигом во времени на один шаг, а выравнивание проводится по полиному второго порядка, то коэффициенты полинома находятся из условия

Учитывая, что для нечетных 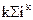 = 0, приходим к системе:
= 0, приходим к системе:

Для определения а0 необходимо найти значения  и
и  .
.
Так как интервал сглаживания равен m = 5, то  = 10 и
= 10 и  =34
=34
Нормальное уравнение, определяющие a0 и а2, в этом случае
записываются так:

Решение этой системы относительно a0 может быть представлено следующим образом:

| (10.23) |
Аналогичным путем получим выражениями для других интервалов сглаживания по параболе второго и третьего порядка. Так, например, для

Согласно приведенным формулам, веса симметричны относительно центрального уровня (yt) и их сумма с учетом общего множителя, вынесенного за скобки, равна единице.
По данным рассмотренного выше примера с урожайностью зерновых получим следующие значения взвешенных скользящих средних для m = 5 (табл. 10.7 гр. 7). Пятичленная скользящая средняя показывает, что на протяжении периода с 1982 по 1997 гг. наблюдался рост урожайности зерновых культур.
Выбор уравнения тренда, отображающего развитие социально-экономических явлений во времени. Для отображения основной тенденции развития явлений во времени применяются полиномы разной степени, экспоненты, логистические кривые и другие функции.
Полиномы имеют следующий вид:
полином первой степени  ;
;
полином второй степени  ;
;
полином третьей степени 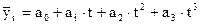 ;
;
полином n-й степени  ,
,
где а0, а1 , а2,… , аn – параметры полиномов; t – условное обозначение времени.
В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр а0 трактуется как характеристика средних условий ряда динамики, параметры а1, а2, а3 – изменение ускорения.
В статистике выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу, полином первой степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны, полиномы второй степени – для отражения ряда динамики с постоянными вторыми разностями (ускорениями), полиномы третьей степени – с постоянными третьими разностями и т. д.
Для полиноминальных моделей характерно отсутствие прямой связи между абсолютными приростами и приростами уровней рядов динамики.
Предполагаемой функцией, отражающей процесс роста явления, может быть и экспонента  или
или  . Экспоненты характеризуют прирост, зависящий от величины основания функции.
. Экспоненты характеризуют прирост, зависящий от величины основания функции.
Отдельные уравнения выражают различные типы динамики. Монотонное возрастание или убывание процесса характеризуют функции: 1) линейная; 2) параболическая; 3) степенная; 4) экспоненциальная простая (показательная) и производная от нее логарифмическая линейная; 5) сложная экспоненциальная и производная от нее логарифмическая парабола; 6) гиперболическая (главным образом убывающих процессов); 7) комбинация их видов.
Для моделирования динамических рядов, проявляющих быстрое развитие в начале ряда и затухающее его развитие к концу, т. е. тех, которые характеризуются стремлением к некоторой предельной величине, применяются логистические функции.
Логистическую функцию часто записывают в следующем виде:
 или
или 
где С – основание натурального логарифма.
Логистическая кривая симметрична относительно точки перегиба и при t = –∞ стремится к нулю, а при t = +∞ стремится к некоторой постоянной величине, к которой кривая асимптотически приближается. Если найти вторую производную от  no t и приравнять ее к нулю, то для логистической кривой, выражаемой через местоположение точки перегиба кривой, t = lga1, : а0;
no t и приравнять ее к нулю, то для логистической кривой, выражаемой через местоположение точки перегиба кривой, t = lga1, : а0;  = n : 2.
= n : 2.
Тип процессов, характеризующийся наличием экстремальных значений, описывается кривой Гомперца, имеющей следующее уравнение:

Возможны четыре варианта этой кривой. Для экономистов наибольшее значение имеет кривая, у которой lga0 < 0 и a1 < 1. Развитие уровня такой кривой имеет следующие этапы. Если коэффициент a1 меньше единицы при отрицательном значении lga0, то на первом этапе прирост кривой незначителен. Он медленно увеличивается по мере роста t, но на следующем этапе прирост увеличивается быстрее, а затем, после точки перегиба, он начинает уменьшаться, и на подходе к линии асимптоты прирост кривой опять незначителен.
Прологарифмировав функцию Гомперца
 ,
,
получим модифицированную экспоненту. Вводя в модифицированной экспоненте величину, обратную  получим логистическую кривую. Следовательно, логистическая кривая имеет сходство с кривой Гомперца. Различие между ними состоит в том, что изменение во времени первых разностей кривой Гомперца асимметрично, a у логистической кривой их изменение во времени имеет симметричный вид, напоминающий нормальное распределение. Для выбора уравнения можно воспользоваться формулой стандартной ошибки
получим логистическую кривую. Следовательно, логистическая кривая имеет сходство с кривой Гомперца. Различие между ними состоит в том, что изменение во времени первых разностей кривой Гомперца асимметрично, a у логистической кривой их изменение во времени имеет симметричный вид, напоминающий нормальное распределение. Для выбора уравнения можно воспользоваться формулой стандартной ошибки
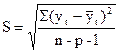 , ,
| (10.24) |
где р – число параметров уравнения,
или применить критерий наименьшей суммы квадратов отклонения эмпирических уровней от теоретических

Из множества возможных уравнений тренда можно выбрать то уравнение, которому соответствует минимальное значение, т. е. критерий наименьших квадратов отклонений, либо использовать формулу средней ошибки аппроксимации:
 . .
| (10.25) |
Все эти характеристики имеют один и тот же смысл: показывают, как близко аналитическая функция выравнивания огибает все значения исходного ряда. Поэтому, проводя сравнительную оценку моделей тренда, можно использовать лишь одну из перечисленных характеристик. Результаты такой оценки, полученные на основе прочих характеристик, как правило, совпадают. Наиболее часто в качестве меры точности аппроксимации выбирают остаточную дисперсию или остаточное среднее квадратическое отклонение.
Расчет параметров полиномов различными методами. После того как выяснен характер кривой развития, необходимо определить ее параметры. Элементарный метод определения параметров уравнения тренда, описанного полиномом или экспонентой, состоит в решении системы уравнений по известным уровням ряда динамики. Если, например, дан ряд динамики, представленный табл. 10.8, то, приняв условные обозначения времени через t и предположение взять две точки – конечный и начальный уровни, можно построить уравнение прямой по этим двум точкам.
Таблица 10.8
Динамика производства готовой продукции на фирме
| 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
| Готовая продукция фирмы, тыс. руб. | 18 | 21 | 26 | 22 | 25 | 28 |
| t | 1 | 2 | 3 | 4 | 5 | 6 |
Уравнение прямой имеет вид:  . Для 2005 г. его уровень составил: а0 + a1 ∙1 = 18; для 2010 г.: а0 + a1 ∙6 = 28.
. Для 2005 г. его уровень составил: а0 + a1 ∙1 = 18; для 2010 г.: а0 + a1 ∙6 = 28.
Решая эти уравнения как систему уравнений, получим: 10 = 5а1; а1 = 2; а0 = 28 – 6а1 = 28 – 12 = 16.. Следовательно, приближенная модель динамики готовой продукции выражается уравнением  = 16 + 2t. Здесь параметр a1 соответствует абсолютному приросту.
= 16 + 2t. Здесь параметр a1 соответствует абсолютному приросту.
Можно предположить и развитие по параболе второго порядка:  , но тогда следует взять три точки, например 2005, 2008, 2010 гг., т. е. уровни при t = 1, t = 4, t = 6.
, но тогда следует взять три точки, например 2005, 2008, 2010 гг., т. е. уровни при t = 1, t = 4, t = 6.
Составим систему трех уравнений с тремя неизвестными:

Решая эту систему, получим: а0 = 18, а1 = 0,3 и а2 = 0,3, а само уравнение применительно к нашему примеру выразится  = 18 + 0,3t + 0,3t2, что в приближенной форме определит модель динамики данного явления.
= 18 + 0,3t + 0,3t2, что в приближенной форме определит модель динамики данного явления.
Отрицательным моментом в таком моделировании тренда служат разные числовые выражения параметров в различных точках их определения.
Другим способом определения параметров уравнения является метод средних значений (линейных отклонений), заключающийся в следующем: ряд расчленяется на две примерно равные части и вводится требование, чтобы сумма выравненных значений в каждой части совпала с суммой фактических значений, т. е. чтобы сумма отклонений фактических данных от выравненных равнялась нулю.
В случае выравнивания по прямой линии  , где а0 и а1 – параметры, получаем:
, где а0 и а1 – параметры, получаем:

| (10.26) |
откуда
 . .
|
Если применить это требование к каждой из двух частей ряда, то, вычисляя для каждой части динамического ряда  и
и 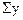 , получим два уравнения с двумя неизвестными. В результате решения этой системы уравнений находим параметры а0 и a1, т. е. начальный уровень и скорость ряда. При этом значение t = 1, 2, 3, 4,..., n.
, получим два уравнения с двумя неизвестными. В результате решения этой системы уравнений находим параметры а0 и a1, т. е. начальный уровень и скорость ряда. При этом значение t = 1, 2, 3, 4,..., n.
Разобьем приведенный в табл. 10.7 ряд динамики урожайности зерновых культур на два периода:
I период – 1992 – 1999 гг.;
II период – 2000 – 2007 гг.,
тогда: Σ1y = 107,5; Σ2y = 124,0; Σ1t = 45; Σ2t = 91.
Для определения параметров а0 и a1 решим систему:

Вычтем из второго уравнения первое. В результате получим: а1 = 0,359; a0= 11,42.
Искомое уравнение будет иметь следующий вид:
 = 11,42 + 0,359t.
= 11,42 + 0,359t.
Метод средних значений прост и требует минимального количества вычислений. Его недостаток заключается в том, что при произвольном расчленении ряда на две части мы будем получать разные результаты. Метод средних значений, как и выравнивание ряда динамики с помощью среднего прироста и темпа роста, может применяться для ориентировочных расчетов.
Выравнивание ряда динамики с помощью метода конечных разностей. Этот метод заключается в следующем.
Пусть ряд динамики yt описывается полиномом р-й степени. Для полинома р-й степени вычислим первые разности:
∆t(1) = yt+1 – yt,
вторые разности:
∆t(2) = y(1)t+1 – yt(1)
и т. д.
Общая формула р-й разности:

| (10.27) |
Любой член уi (i = 0, 1, 2, 3,…, n) ряда динамики можно выразить через начальный уровень ряда у0 и конечные разности:
 ;
;  ,
,
но  , поэтому
, поэтому  и т. д. Отсюда получаем:
и т. д. Отсюда получаем:

| (10.28) |
Если первые разности не равны, но варьируют с незначительными отклонениями друг от друга, а средняя арифметическая вторых разностей настолько мала, что ею можно пренебречь, то первые разности можно считать практически равными.
Окончательная формула для расчета уровней ряда динамики при равных или почти равных первых разностях будет:

| (10.29) |
Если, анализируя вторые разности, мы придем к выводу, что они практически равны, то, вычисляя коэффициенты параболы второго порядка, получаем тренд ряда динамики:
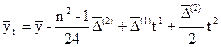
| (10.30) |
где  – выравненное значение ряда динамики;
– выравненное значение ряда динамики;  – средний уровень ряда динамики;
– средний уровень ряда динамики;  – средняя арифметическая первых разностей;
– средняя арифметическая первых разностей;  – средняя арифметическая вторых разностей; n – число уровней; t – независимая переменная (время).
– средняя арифметическая вторых разностей; n – число уровней; t – независимая переменная (время).
Рассмотрим следующий пример (табл. 10.9).
Таблица 10.9
Сглаживание удельного веса прибытия воздушных судов, выполненных без опоздания по сравнению с расписанием одной из авиакомпаний за 2000 – 2010 гг. методом конечных разностей
| Год | Удельный вес прибы- тий, yt, %
| Условное обозначе- ние време- ни t | Разности | Выравнен- ные значе- ния | |
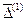
| 
| ||||
| 2000 | 91,6 | -5 | - | - | 91,6 |
| 2001 | 91,5 | -4 | -0,1 | - | 91,4 |
| 2002 | 91,3 | -3 | -0,2 | -0,1 | 91,3 |
| 2003 | 91,1 | -2 | -0,2 | 0 | 91,1 |
| 2004 | 91,0 | -1 | -0,1 | 0,1 | 91,0 |
| 2005 | 90,8 | 0 | -0,2 | -0,1 | 90,8 |
| 2006 | 90,6 | 1 | -0,2 | 0 | 90,6 |
| 2007 | 90,4 | 2 | -0,2 | 0 | 90,4 |
| 2008 | 90,2 | 3 | -0,2 | 0 | 90,2 |
| 2009 | 90,0 | 4 | -0,2 | 0 | 90,1 |
| 2010 | 89,9 | 5 | -0,1 | 0,1 | 89,9 |
| Итого | 998,4 | 0 | -1,7 | 0,0 | 998,4 |
Средние
значения

| 90,76 | - | -0,17 | - | - |
Способом конечных разностей получили уравнение, выражающее тенденцию динамики данного в ряде процесса:
 = 90,76 – 0,17t.
= 90,76 – 0,17t.
Метод наименьших квадратов при расчете параметров полиномов. Этот метод при моделировании рядов динамики можно рассматривать как некоторый прием получения оценки детерминированной компоненты f(t), которая характеризует тренд изучаемого явления.
В экономике часто применяется функция вида:

| (10.31) |
Отсюда а0, а1, а2,… , ар в формулах находятся методом наименьших квадратов, сущность которого нам известна из регрессионного анализа.
Согласно этому методу, для нахождения параметров полинома р-й степени необходимо решить систему так называемых нормальных уравнений:

| (10.32) |
где n – число членов в ряду динамики; t = 1, 2, ... .
Система (10.32), состоящая из «р» уравнений, содержит в качестве известных величин Σу, Σуt, ..., Σуtp, т. е. суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 0, 1, 2, ..., р, и «р» неизвестных величин аi,. Решение этой системы относительно а0, а1,… , ар и дает искомые значения параметров.
Системы для расчета параметров полиномов невысоких степеней намного проще. Обозначим последовательные параметры полиномов как а0, а1, а2. Тогда системы нормальных уравнений для оценивания параметров прямой (  ) примут вид:
) примут вид:

| (10.33) |
для параболы второго порядка (  ).
).

| (10.34) |
Решение системы (10.33) относительно искомых параметров а0 и а1:

|
Аналогичным путем можно было бы подойти и к системе (10.34). Однако такой путь расчета параметров достаточно трудоемок, если он не выполняется на ЭВМ. Поэтому перейдем к упрощенным приемам расчета параметров, применение которых дает ощутимую экономию труда без какой-либо потери точности результатов.
Упрощенный расчет параметров уравнений заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат t было равно 1, 2, 3, ..., n, то после переноса t = ... -4, -3,
-2, -1, 0, 1, 2, 3, 4,..., если число членов ряда нечетное. Когда же число ряда четное, то
t = ..., -5, -3, -1, 1, 3, 5,... Следовательно, Σt и все Σtр, у которых «р» – нечетное число, равны 0. Таким образом, все члены уравнений, содержащие Σt с такими степенями, могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой;

| (10.35) |
для параболы второго порядка:

| (10.36) |
Решая системы (10.35), (10.36) относительно неизвестных параметров, получим величины параметров соответствующих полиномов.
Параметр a1 выражает начальную скорость роста, а коэффициент а2 – постоянную скорость изменения прироста. Если уровень явления растет с ускорением, то величина этого ускорения в среднем за изучаемый период равна 2а2 единицам.
При сглаживании ряда динамики по экспоненте (  ) для определения параметров применяется метод наименьших квадратов к логарифмам исходных данных. Так, для нахождения параметров экспоненты необходимо решить следующую систему уравнений:
) для определения параметров применяется метод наименьших квадратов к логарифмам исходных данных. Так, для нахождения параметров экспоненты необходимо решить следующую систему уравнений:
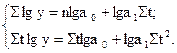
| (10.37) |
Если  = 0, то параметры уравнения lga0 и lga1 находим по формулам:
= 0, то параметры уравнения lga0 и lga1 находим по формулам: 

Экспонента отражает постоянный относительный рост, равный ea1 единицам. Рассмотрим следующий пример. Необходимо определить основную тенденцию ряда динамики урожайности зерновых культур в хозяйстве за 1983 – 1997 гг. по данным табл. 10.10.
Начнем определение тенденции с самого простого полинома – уравнения прямой (10.35). Решая систему нормальных уравнений, получим искомые параметры: а0 = 14,8; а1 = 0,17. А само уравнение представим следующим образом:  = 14,8 + 0,17t, которое показывает тенденцию динамики урожайности зерновых культур в 1993 – 2007 гг., т. е. в течение исследуемого периода урожайность зерновых культур в хозяйстве увеличилась в среднем на 0,17 ц/га в год.
= 14,8 + 0,17t, которое показывает тенденцию динамики урожайности зерновых культур в 1993 – 2007 гг., т. е. в течение исследуемого периода урожайность зерновых культур в хозяйстве увеличилась в среднем на 0,17 ц/га в год.
Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции или наблюдается автокорреляция не в самих уровнях, а в их отклонениях от полученных по определенным аналитическим формулам теоретических значений. В таких случаях следует использовать гармонический анализ.
Целью данного анализа являются выявление и измерение периодических колебаний в рядах динамики и автокорреляции в остатках ряда.
Функцию, заданную в каждой точке изучаемого интервала времени, можно представить бесконечным рядом синусоидальных и косинусоидальных функций. Нахождение конечной суммы уровней с использованием функций косинусов и синусов времени называется гармоническим анализом.
Другими словами, гармонический анализ представляет собой операцию по выражению заданной периодической функции в виде ряда Фурье по гармоникам разных порядков. Каждый член ряда представляет собой слагаемое постоянной величины с функциями косинусов и синусов определенного периода.
Таблица 10.10
Динамика урожайности зерновых: культур в хозяйстве и определение параметров уравнения методом наименьших квадратов
| Год | Урожай- ность, ц с 1 га, Уi, | t | t2 | Уit | 
|
| 1993 | 13,7 | -7 | 49 | -95,9 | 13,6 |
| 1994 | 12,1 | -6 | 36 | -72,6 | 13,8 |
| 1995 | 14,0 | -5 | 25 | -70,0 | 13,9 |
| 1996 | 13,2 | -4 | 16 | -52,8 | 14,1 |
| 1997 | 15,6 | -3 | 9 | -46,8 | 14,3 |
| 1998 | 15,4 | -2 | 4 | -30,8 | 14,5 |
| 1999 | 34,0 | -1 | 1 | -14,0 | 14,6 |
| 2000 | 17,6 | 0 | 0 | 0 | 14,8 |
| 2001 | 15,4 | 1 | 1 | 15,4 | 15,0 |
| 2002 | 10,9 | 2 | 4 | 21,8 | 15,1 |
| 2003 | 17,5 | 3 | 9 | 52,5 | 15,3 |
| 2004 | 15,0 | 4 | 16 | 60,0 | 15,5 |
| 2005 | 18,5 | 5 | 25 | 92,5 | 15,7 |
| 2006 | 14,2 | 6 | 36 | 85,2 | 15,8 |
| 2007 | 14,9 | 7 | 49 | 104,3 | 16,0 |
| Итого | 222,0 | 0 | 280 | 48,8 | 222,0 |
В простейшем случае динамика явлений, обладающих периодичностью, может быть аппроксимирована синусоидой:
Y = A sin (at + b),
где t – время; А – полуамплитуда колебания, т. е. наибольшее и наименьшее отклонения от оси t; t = π / a – период (длина волны) колебательного движения; b – начальная фаза колебания.
При t = 0 получаем yt=0 = A sinb.
Аппроксимация динамики экономических явлений рядом Фурье состоит в выборе таких гармонических колебаний, наложение которых друг на друга (сумма) отражало бы периодические колебания фактических уровней динамического ряда. С помощью ряда Фурье можно представить динамику явлений в виде некоторой функции времени, в которой слагаемые расположены по убыванию периодов:
 . .
| (10.38) |
В этом уравнении величина k определяет гармонику ряда Фурье и может быть взята целым числом (чаще всего от 1 до 4), Параметры уравнения рассчитываются методом наименьших квадратов.
Найдя частные производные этой функции и приравняв их к нулю, получим систему нормальных уравнений, из которой вычислим параметры:
 ;
; 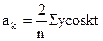 ;
;  .
.
Последовательные значения t обычно определяются от 0 с увеличением (приростом), равным 2π/n, где n – число уровней ряда динамики.
Для изучения специфического периодического явления – сезонности берется n = 12, по числу месяцев в году.
Тогда ряд динамики годового производства можно записать так:

Для определенных в каждом конкретном случае t находят значения синусов и косинусов разных гармоник, которые для удобства располагают в табл. 10.11.
Таблица 10.11
Коэффициент гармонического анализа месячных наблюдений для расчета параметров аk и bk
| t | cost | cos2t | cos3t | cos4t | sint | sin2t | sm3t | sin4t |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| π/6 | 0,866 | 0,5 | 0 | -0,5 | 0,5 | 0,866 | 1 | 0,866 |
| π/3 | 0,5 | -0,5 | -1 | -0,5 | 0,866 | 0,866 | 0 | -0,866 |
| π/2 | 0 | -1 | 0 | 1 | 1 | 0 | -1 | 0 |
| 2π/3 | -0,5 | -0,5 | 1 | -0,5 | 0,866 | -0,866 | 0 | 0,866 |
| 5π/6 | -0,866 | 0,5 | 0 | -0,5 | 0,5 | -0,866 | 1 | -0,866 |
| π | -1 | 1 | -1 | 1 | 0 | 0 | 0 | 0 |
| 7π/6 | -0,866 | 0,5 | 0 | -0,5 | -0,5 | 0,866 | -1 | 0,866 |
| 4π/3 | -0,5 | -0,5 | 1 | -0,5 | -0,866 | 0,866 | 0 | -0,866 |
| 3π/2 | 0 | -1 | 0 | 1 | -1 | 0 | 1 | 0 |
| 5π/3 | 0,5 | -0,5 | -1 | -0,5 | -0,866 | -0,866 | 1 | 0,866 |
| 11π/6 | 0,866 | 0,5 | 0 | -0,5 | -0,5 | -0,866 | -1 | - 0,866 |
Полагая гармоники k соответственно равными 1, 2, 3 и т. д., находим все значения coskt и sinkt Тогда, например, первая гармоника ряда Фурье примет вид:
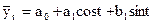
здесь:
 ; ;  ; ; 
| (10.39) |
Ряд Фурье с двумя гармониками:

| (10.40) |
где 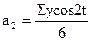 ;
;  .
.
|
из
5.00
|
Обсуждение в статье: Методы анализа основной тенденции (тренда) в рядах динамики |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


