 |
Главная |
Евклидово пространство
|
из
5.00
|
Выше мы ввели понятие линейного векторного пространства, в котором определены операции сложения векторов и умножения их на число, а также ввели понятия размерности и базиса этого пространства. Теперь дополним это пространство метрикой, т.е. укажем способы измерения длин векторов и углов между ними. Это можно сделать, доопределив в векторном пространстве понятие скалярного произведения векторов, естественно, обобщив его на случай n-мерных векторов.
Определение. Скалярным произведением двух векторов  и
и  называется число, равное:
называется число, равное:

Отметим основные свойства скалярного произведения, которые непосредственно вытекают из сформулированного определения.
 - коммутативное свойство;
- коммутативное свойство;
 - дистрибутивное свойство;
- дистрибутивное свойство;
 - свойство справедливое для любого действительного α;
- свойство справедливое для любого действительного α;
 , если
, если  , и
, и  , если
, если  .
.
Определение. Линейное векторное пространство, в котором определено скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, рассматриваемым как аксиомы, называется евклидовым пространством.
Определение. Длиной или нормой вектора  в n-мерном евклидовом пространстве называется корень квадратный из его скалярного квадрата, т.е.:
в n-мерном евклидовом пространстве называется корень квадратный из его скалярного квадрата, т.е.:

Определенная таким образом норма вектора обладает некоторыми свойствами, основное из которых записывается в виде:  и носит название неравенства Коши-Буняковского.
и носит название неравенства Коши-Буняковского.
Очевидно, что косинус угла j между двумя векторами  и
и  можно определить равенством, непосредственно вытекающим из неравенства Коши-Буняковского:
можно определить равенством, непосредственно вытекающим из неравенства Коши-Буняковского:
 , где:
, где: 
Определение. Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Определение. Векторы 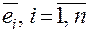 n-мерного евклидова пространства Rn образуют ортонормированный базис, если они попарно ортогональны, и норма каждого из них равна единице.
n-мерного евклидова пространства Rn образуют ортонормированный базис, если они попарно ортогональны, и норма каждого из них равна единице.
Существует теорема, устанавливающая одно из основных свойств евклидова пространства.
| Во всяком n-мерном евклидовом пространстве существует ортонормированный базис. |
Примером одного из таких ортонормированных базисов является система из n единичных векторов, у которых i-ая компонента равна 1, а все остальные компоненты равны нулю, т.е. базис из векторов:  и т.д.
и т.д.
Линейные операторы
Если задан закон (правило), по которому каждому вектору  пространства Rn ставится в соответствие единственный вектор
пространства Rn ставится в соответствие единственный вектор  этого же пространства, то говорят, что задан оператор (преобразование, отображение)
этого же пространства, то говорят, что задан оператор (преобразование, отображение)  и записывают
и записывают  .
.
Оператор  называется линейным, если для любых векторов
называется линейным, если для любых векторов  и
и 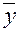 пространства Rn и любого действительного числа λ выполняются соотношения:
пространства Rn и любого действительного числа λ выполняются соотношения:
 - свойство аддитивности оператора;
- свойство аддитивности оператора;
 - свойство однородности оператора.
- свойство однородности оператора.
Опираясь на свойства линейности оператора, можно показать, что его воздействие на вектор  состоит в том, что матрица-столбец координат этого вектора (в некотором базисе) умножается слева на квадратную матрицу А оператора и в результате получается матрица-столбец координат вектора
состоит в том, что матрица-столбец координат этого вектора (в некотором базисе) умножается слева на квадратную матрицу А оператора и в результате получается матрица-столбец координат вектора 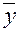 (в том же базисе), т.е. Y = AX. Другими словами, каждому линейному оператору можно поставить в соответствие единственную квадратную матрицу этого оператора.
(в том же базисе), т.е. Y = AX. Другими словами, каждому линейному оператору можно поставить в соответствие единственную квадратную матрицу этого оператора.
При переходе к другому базису в пространстве Rn матрица линейного оператора изменится. Можно показать, что матрицы А* и А линейного оператора  в новом базисе
в новом базисе  и в старом базисе
и в старом базисе  , соответственно, связаны соотношением:
, соответственно, связаны соотношением:  , где С – матрица перехода от старого базиса к новому (см. подраздел 3.4).
, где С – матрица перехода от старого базиса к новому (см. подраздел 3.4).
Определение. Ненулевой вектор  называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  (или линейного преобразования, заданного матрицей А), если существует такое число λ, что справедливо равенство:
(или линейного преобразования, заданного матрицей А), если существует такое число λ, что справедливо равенство:  . При этом число λ называется собственным значением оператора
. При этом число λ называется собственным значением оператора  (или матрицы А), соответствующим собственному вектору
(или матрицы А), соответствующим собственному вектору  .
.
Из приведенного определения следует, что собственный вектор под воздействием линейного оператора переходит в вектор, коллинеарный самому себе, т.е. просто умножается на число – собственное значение, ему соответствующее.
Характеристическим уравнением матрицы А линейного оператора называется уравнение:
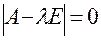 . .
|
где λ – неизвестное собственное значение, Е – единичная матрица.
ПРИМЕР: Для матрицы

характеристическое уравнение будет иметь вид:
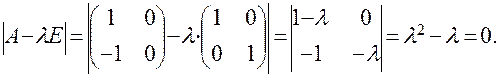
Таким образом, задача отыскания собственных векторов и собственных значений линейного оператора решается в следующей последовательности. Вначале составляют и решают характеристическое уравнение. Его решениями будут собственные значения, причем их количество не превосходит n. После этого, подставляя последовательно каждое из найденных собственных значений в систему однородных уравнений вида:

каждый раз решают ее методом Гаусса и выясняют структуру нетривиальных решений – координат собственного вектора, соответствующего данному собственному значению.
ПРИМЕР: Найдите собственные векторы линейного оператора, заданного матрицей:

Составим характеристическое уравнение для отыскания собственных значений:

Решениями этого уравнения будут два собственных значения преобразования А: λ1 = 2 и λ2 = − 1.
Приступим к отысканию собственного вектора, соответствующего первому из собственных значений. Для этого запишем систему однородных уравнений:

Полученная система фактически представляет собой одно уравнение с двумя неизвестными. Положим  и найдем
и найдем  . Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты:
. Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты:
 ,
,
где С1 – любое действительное число, отличное от нуля.
Для второго собственного значения система однородных уравнений запишется в виде:

Т.е. представляет собой одно уравнение с двумя неизвестными. Полагая  , найдем
, найдем  , и окончательно запишем:
, и окончательно запишем:
 ,
,
где С2 – любое действительное число, отличное от нуля.
|
из
5.00
|
Обсуждение в статье: Евклидово пространство |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

