 |
Главная |
Однофакторный дисперсионный анализ
|
из
5.00
|
Однофакторная дисперсионная модель имеет вид:
 ,
,
Где  -значение исследуемой переменной, полученной на
-значение исследуемой переменной, полученной на  -м уровне фактора (
-м уровне фактора ( 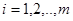 ) с
) с  -м порядковым номером (
-м порядковым номером ( 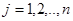 );
);
 - общая средняя;
- общая средняя;
 - эффект, обусловленный влиянием
- эффект, обусловленный влиянием 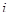 -го уровня фактора, т.е. вариация переменной между отдельными уровнями фактора;
-го уровня фактора, т.е. вариация переменной между отдельными уровнями фактора;
 -случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариация переменной внутри отдельного уровня фактора.
-случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариация переменной внутри отдельного уровня фактора.
Под уровнем фактора понимается некоторая его мера или состояние, например номер партии детали, количество вносимых удобрений и т.п.
Проверим существенность влияния № партий изделий на их качество. Пусть имеется  партий изделий. Из каждой партии отобрано соответственно
партий изделий. Из каждой партии отобрано соответственно  изделий (положим, что
изделий (положим, что  ). Значения показателей качества этих изделий представим в виде матрицы (или таблицы):
). Значения показателей качества этих изделий представим в виде матрицы (или таблицы):

Если полагать, что элементы строк матрицы наблюдений – это численные значения (реализации) случайных величин 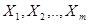 , выражающих качество изделий и имеющих нормальный закон распределения с математическим ожиданием соответственно
, выражающих качество изделий и имеющих нормальный закон распределения с математическим ожиданием соответственно 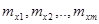 и одинаковыми дисперсиями
и одинаковыми дисперсиями  , то данная задача сводится к проверке нулевой гипотезы
, то данная задача сводится к проверке нулевой гипотезы  :
:  .
.
Предположим, что для каждой  -ой партии(
-ой партии(  -го уровня фактора) из
-го уровня фактора) из  изделий имеем средний показатель качества
изделий имеем средний показатель качества  , равный сумме общего среднего
, равный сумме общего среднего  и ее вариации
и ее вариации  , обусловленной
, обусловленной 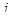 -ым уровнем фактора:
-ым уровнем фактора:
 ,
,
называемая группой средней для  -го уровня фактора.
-го уровня фактора.
Очевидно, что оценкой  является средняя арифметическая
является средняя арифметическая  из
из  изделий
изделий  -ой партии (
-ой партии (  -го уровня фактора):
-го уровня фактора):
 .
.
Оценкой общего среднего 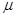 является средняя арифметическая всей совокупности показателей качества:
является средняя арифметическая всей совокупности показателей качества:
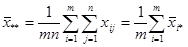 .
.
Рассмотрим сумму квадратов отклонений  от общей средней
от общей средней  в виде :
в виде :

Или  :
:
где  - сумма квадратов отклонений групповых средних от общей средней, или межгрупповая (факторная) сумма квадратов отклонений;
- сумма квадратов отклонений групповых средних от общей средней, или межгрупповая (факторная) сумма квадратов отклонений;
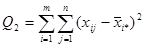 - сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений.
- сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений.
В разложении общей суммы квадратов отклонений 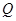 заключенная основная идея дисперсионного анализа: общая вариация показателя качества, измеренная суммой
заключенная основная идея дисперсионного анализа: общая вариация показателя качества, измеренная суммой 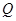 , складывается из двух компонент -
, складывается из двух компонент -  и
и  , характеризующих изменчивость этого показателя между партиями (
, характеризующих изменчивость этого показателя между партиями (  ) под воздействием изучаемого фактора и изменчивость «внутри» партий (
) под воздействием изучаемого фактора и изменчивость «внутри» партий (  ) под воздействием всех других неучтенных факторов. В дисперсионном анализе изменчивость показателя оценивается не по суммам квадратов отклонений, а по выборочным дисперсиям
) под воздействием всех других неучтенных факторов. В дисперсионном анализе изменчивость показателя оценивается не по суммам квадратов отклонений, а по выборочным дисперсиям  , которые являются несмещенными оценками соответствующих дисперсий генеральных совокупностей:
, которые являются несмещенными оценками соответствующих дисперсий генеральных совокупностей:

 ,
,
 ,
,
где 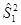 и
и 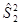 - получили название межгрупповой и внутригрупповой дисперсиями.
- получили название межгрупповой и внутригрупповой дисперсиями.
Доказано, что, если влияние всех уровней фактора 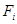 на показатели качества (для нашего примера) одинаково, то
на показатели качества (для нашего примера) одинаково, то 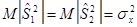 . Иными словами, межгрупповая и внутригрупповая дисперсии являются несмещенными оценками общей дисперсии генеральной совокупности и проверка нулевой гипотезы
. Иными словами, межгрупповая и внутригрупповая дисперсии являются несмещенными оценками общей дисперсии генеральной совокупности и проверка нулевой гипотезы  сводится к проверки
сводится к проверки 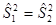 . Для этого вычисляется критерий (статистика):
. Для этого вычисляется критерий (статистика):
 .
.
При правильности нулевой гипотезы  критерий
критерий  должен подчиняться закону распределения Фишера со степенями свободы
должен подчиняться закону распределения Фишера со степенями свободы 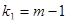 и
и  . Поэтому при заданном уровне значимости
. Поэтому при заданном уровне значимости  критическое значение
критическое значение 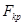 критерия находим по таблицам
критерия находим по таблицам 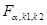 закона распределения Фишера.
закона распределения Фишера.
Если 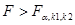 , то нулевая гипотеза отвергается и делается заключение о существенности влияния фактора
, то нулевая гипотеза отвергается и делается заключение о существенности влияния фактора 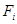 на случайную величину.
на случайную величину.
При  нет оснований отвергать гипотезу
нет оснований отвергать гипотезу  и считают, что влияние фактора несущественно.
и считают, что влияние фактора несущественно.
Кроме того, по величине отношения  судят, насколько сильно проявляется влияние фактора.
судят, насколько сильно проявляется влияние фактора.
Для упрощения расчетов сумм квадратов 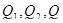 удобно пользоваться следующими формулами, которые позволяют предварительно не находить средние значения
удобно пользоваться следующими формулами, которые позволяют предварительно не находить средние значения  и
и  :
:
 ,
,  .
.
|
из
5.00
|
Обсуждение в статье: Однофакторный дисперсионный анализ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

