 |
Главная |
Теорема Чебышева (закон больших чисел).
|
из
5.00
|
Теорема: Если 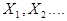 последовательность независимых случайных величин, которые имеют
последовательность независимых случайных величин, которые имеют
конечное математические ожидания и ограниченные дисперсии 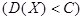 , то
, то
средние арифметические наблюденных значений случайных величин сходиться по
вероятности к среднему арифметическому их математических ожиданий:
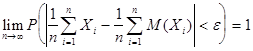 .
.
Закон больших чисел справедлив и для зависимых случайных величин, то есть справедлива
теорема Маркова:
Теорема: : Если для случайных величин 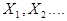 выполняется условие
выполняется условие
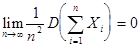 , то среднее арифметическое наблюденных случайных величин
, то среднее арифметическое наблюденных случайных величин
сходится по вероятности к среднему арифметическому их математических ожиданий:
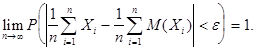
Теоремы Бернулли : Если производится 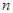 испытаний, в каждом из которых некоторое событие
испытаний, в каждом из которых некоторое событие
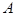 может появиться с вероятностью
может появиться с вероятностью 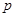 , то относительная частота появления
, то относительная частота появления
события в 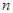 испытаниях сходится по вероятности к вероятности появления
испытаниях сходится по вероятности к вероятности появления
события в каждом испытании:
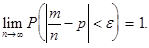
Теорема Пуассона: Пусть производится 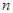 независимых испытаний, в каждом их которых событие
независимых испытаний, в каждом их которых событие
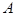 появляется с вероятностью
появляется с вероятностью 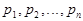 . Тогда при неограниченном
. Тогда при неограниченном
увеличении числа испытаний относительная частота появления события 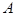
сходится по вероятности к среднему арифметическому вероятности
появления события в различных испытаниях:
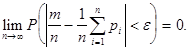
Теорема Лендеберга-Леви: Пусть 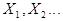 независимые одинаково распределенные случайные
независимые одинаково распределенные случайные
величины с математическим ожиданием 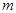 и дисперсией
и дисперсией 
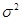 . Закон
. Закон
распределения нормируемой случайной величины 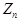 стремится к нормальному
стремится к нормальному
закону распределения с плотностью распределения вероятностей равной
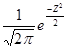 ,
, 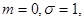 где
где
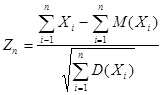 - нормированная случайная величина.
- нормированная случайная величина.
Это центральная предельная теорема для одинаково распределенных случайных независимых величин.
Теорема Ляпунова: Если 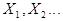 независимые случайные величины, имеющие конечные
независимые случайные величины, имеющие конечные
математические ожидания 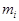 и дисперсии
и дисперсии 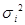 и абсолютные центральные
и абсолютные центральные
моменты третьего порядка, удовлетворяющие условиям:
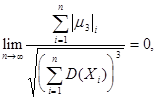
то закон распределения величины 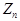 сходится к нормальному закону
сходится к нормальному закону
распределения с плотностью распределения вероятности
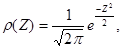 для которой
для которой 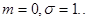
Эта теорема имеет большое практическое значение, так как, используя ее, можно вычислить вероятность того, что сумма независимых случайных величин принимает значение, принадлежащее интервалу. Условие
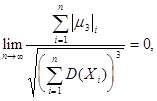 характеризует тот факт, что все случайные величины сравнимы между собой, то есть ни одна из случайных величин не имеет преимущество перед другими случайными величинами.
характеризует тот факт, что все случайные величины сравнимы между собой, то есть ни одна из случайных величин не имеет преимущество перед другими случайными величинами.
Рассмотрим дискретную случайную величину 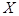 , которая характеризует число появлений события
, которая характеризует число появлений события 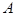 в
в 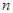 независимых испытаниях. Эту случайную величину можно представить в виде суммы случайной величины
независимых испытаниях. Эту случайную величину можно представить в виде суммы случайной величины 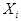 , каждая из которых характеризует число появлений события
, каждая из которых характеризует число появлений события 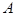 в
в 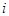 испытании. Нормированная сумма будет иметь вид:
испытании. Нормированная сумма будет иметь вид: 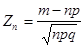 .
.
Если случайная величина 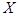 подчиняется биноминальному закону распределения, то вычисление вероятности того, что некоторое событие
подчиняется биноминальному закону распределения, то вычисление вероятности того, что некоторое событие 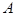 появиться
появиться 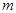 раз в
раз в 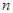 испытаниях по формуле Бернулли затруднительно, если
испытаниях по формуле Бернулли затруднительно, если 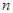 достаточно большое, а
достаточно большое, а 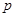 мало. В этом случае можно воспользоваться следующими теоремами:
мало. В этом случае можно воспользоваться следующими теоремами:
Теорема Мавра -Лапласа (локальная): Пусть производится 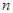 испытаний, в каждом из которых
испытаний, в каждом из которых
некоторое событие 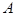 может появиться с вероятностью
может появиться с вероятностью 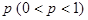 . Тогда для всех
. Тогда для всех 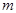 , удовлетворяющих условию
, удовлетворяющих условию 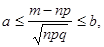 ( где
( где 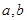 - произвольные числа) выполняется соотношение:
- произвольные числа) выполняется соотношение:
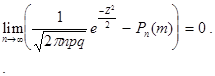
Локальная теорема используется при больших значениях 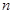 для вычисления
для вычисления 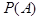 , где некоторое событие
, где некоторое событие 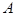 наступает
наступает 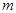 раз в
раз в 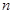 испытаниях.
испытаниях.
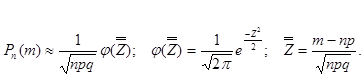
Теорема Муавра- Лапласа (интегральная): Пусть производится 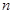 независимых испытаний,
независимых испытаний,
в каждом из которых событие может появиться с вероятностью 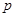 . Тогда для любых
. Тогда для любых 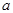 и
и 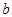
справедливо соотношение:
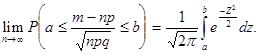
Из предельного равенства теоремы следует формула:
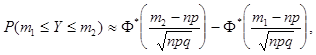
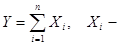 число появлений событий
число появлений событий 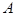 в
в 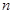 испытаниях.
испытаниях.
Отсюда вытекают следующие соотношения:
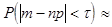 2Ф*
2Ф* 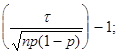
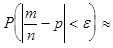 2Ф*
2Ф* 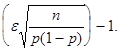
В отличии от теорем Бернулли и Пуассона последние две формулы более точную оценку
вероятности отклонений частоты появления событий от его математического ожидания и
частости события от вероятности появления события в каждом испытании.
Двумерные случайные величины.
Совокупность случайных величин 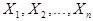 образуют
образуют 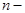 мерную случайную
мерную случайную
величину 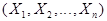 . Если экономический процесс описывается при помощи двух
. Если экономический процесс описывается при помощи двух
случайных величин 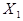 и
и 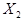 , определяется двумерная случайная величина
, определяется двумерная случайная величина 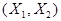 или
или
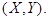
Функция распределения системы двух случайных величин 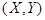 , рассматриваемой как
, рассматриваемой как
функция переменных 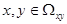 , называется вероятность появления события
, называется вероятность появления события
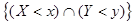 :
:
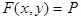
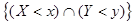 .
.
Используя функцию распределения, можно найти вероятность попадания случайной точки в
бесконечную полуполосу 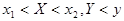 или
или 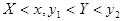 и прямоугольник
и прямоугольник
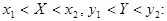
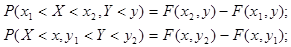
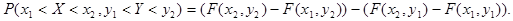
Дискретной называют двухмерную величину, составляющие которой дискретны.
Законом распределения двумерной дискретной случайной величины называется множество
всевозможных значений 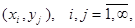 дискретных двумерных случайных величин и
дискретных двумерных случайных величин и
соответствующих им вероятностей 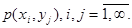 При этом
При этом 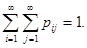
Непрерывной называют двумерную величину, составляющие которой непрерывны.
Функция 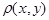 , равная пределу отношения вероятности попадания двумерной случайной
, равная пределу отношения вероятности попадания двумерной случайной
величины 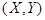 в прямоугольник со сторонами
в прямоугольник со сторонами 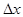 и
и 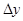 к площади этого прямоугольника,
к площади этого прямоугольника,
когда обе стороны прямоугольника стремятся к нулю, называется плотностью распределения
вероятностей:
 .
.
Зная плотность распределения, можно найти функцию распределения по формуле:
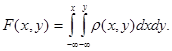
Вероятность попадания случайной точки 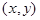 в область
в область 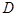 определяется равенством:
определяется равенством:
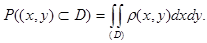
Вероятность того, что случайная величина 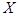 приняла значение
приняла значение 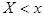 при условии, что
при условии, что
случайная величина 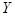 приняла фиксированное значение, вычисляется по формуле:
приняла фиксированное значение, вычисляется по формуле:
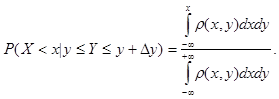
Начальным моментом порядка 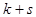 системы
системы 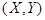 называется математическое
называется математическое
ожидание произведений 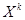 и
и 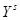 , т.е.
, т.е. 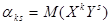 .Если
.Если  и
и 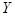 -дискретные
-дискретные
случайные величины, то
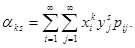
Если 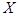 и
и 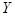 - непрерывные случайные величины, то
- непрерывные случайные величины, то
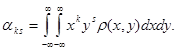
Центральным моментом порядка 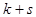 системы
системы 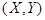 называется математическое
называется математическое
ожидание произведений 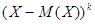 и
и 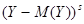 , т.е.
, т.е.
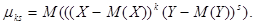
Если составляющие величины являются дискретными, то
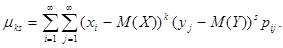
Если составляющие величины являются непрерывными, то
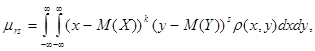 где
где
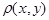 - плотность распределения системы
- плотность распределения системы 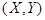 .
.
Условным математическим ожиданием 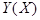 при
при 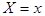 ( при
( при 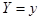 ) называется
) называется
выражение вида:
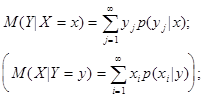 -для дискретной случайной величины
-для дискретной случайной величины 
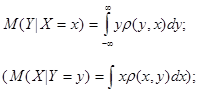 - для непрерывной случайной величины
- для непрерывной случайной величины 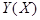 .
.
Корреляционным моментом независимых случайных величин 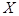 и
и 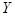 , входящих в
, входящих в
двумерную случайную величину 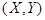 , называют математическое ожидание произведений
, называют математическое ожидание произведений
отклонений этих величин:
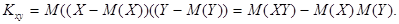
Корреляционный момент двух независимых случайных величин 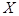 и
и 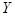 , входящих в
, входящих в
двумерную случайную величину 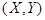 , равен нулю.
, равен нулю.
Коэффициентом корреляции 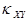 случайных величин
случайных величин 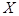 и
и 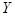 , входящих в
, входящих в
двумерную случайную величину 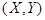 , называют отношение корреляционного момента к
, называют отношение корреляционного момента к
произведению средних квадратических отклонений этих величин:
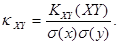
Коэффициент корреляции удовлетворяет условию 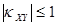 и определяет степень линейной
и определяет степень линейной
зависимости между 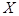 и
и 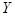 . Случайные величины, для которых
. Случайные величины, для которых 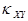 =0 , называются
=0 , называются
некоррелированными.
Уравнения 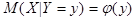 и
и 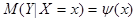 называют уравнениями регрессии, а линии, определяемые ими, - линиями регрессии.
называют уравнениями регрессии, а линии, определяемые ими, - линиями регрессии.
Лекция №9.Случайные функции. Цепи Марков. Пуассоновский поток событий
Пусть 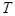 - некоторое множество действительных чисел. Если каждому значению
- некоторое множество действительных чисел. Если каждому значению 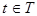 поставлена в соответствие случайная величина
поставлена в соответствие случайная величина 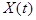 , то на множестве
, то на множестве 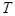 задана случайная функция
задана случайная функция 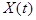 .
.
Если 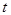 - время, то случайная функция называется случайным процессом.
- время, то случайная функция называется случайным процессом.
Значение случайной функции 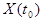 при
при 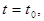 где
где 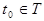 , называется сечением. Каждое испытание дает конкретную функцию
, называется сечением. Каждое испытание дает конкретную функцию 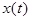 , которая называется реализацией (траекторией) случайной функции.
, которая называется реализацией (траекторией) случайной функции.
 X X сечение
X X сечение
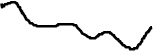 |


0 t 0 t t
Реализация Семейство реализаций
При зафиксированном значении аргумента t случайная функция X(t) превращается в случайную величину- сечение случайной функции или процесса. Тогда X(t) в данный момент времени t определяется плотностью распределения f(x ; t). Однако одномерные законы распределения и их числовые характеристики, вычисленные для одного момента времени ( для одного сечения семейства реализаций) не могут оценивать характер изменения процесса во времени. Для этой цели используют характеристики связи между ординатами, взятыми в различные моменты времени. Наиболее полно эти связи характеризуются многомерной плотностью распределения 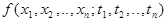 n произвольных сечений процесса. Однако многомерная плотность распределения не всегда известна, поэтому для практических приложений случайные процессы характеризуются математическим ожиданием, дисперсией и корреляционной функцией.
n произвольных сечений процесса. Однако многомерная плотность распределения не всегда известна, поэтому для практических приложений случайные процессы характеризуются математическим ожиданием, дисперсией и корреляционной функцией.
Математическим ожиданием случайной функцией 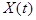 называют неслучайную функцию
называют неслучайную функцию 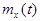 , которая при каждом значении аргумента
, которая при каждом значении аргумента 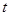 равна математическому ожиданию соответствующего сечения семейства реализаций случайной функции:
равна математическому ожиданию соответствующего сечения семейства реализаций случайной функции:
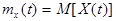
и является средней траекторией для всех возможных реализаций.
Дисперсией случайной функции 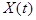 называют неслучайную функцию
называют неслучайную функцию 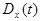 , значения которой для каждого
, значения которой для каждого 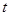 равно дисперсии соответствующего сечения случайной функции:
равно дисперсии соответствующего сечения случайной функции:
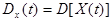
и характеризующей возможный разброс реализаций случайной функции относительно средней траектории.
Корреляционной функцией случайной функции 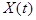 называют неслучайную функцию двух аргументов
называют неслучайную функцию двух аргументов 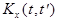 , которая при каждой паре значений
, которая при каждой паре значений 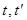 равна корреляционному моменту соответствующих сечений случайной функции:
равна корреляционному моменту соответствующих сечений случайной функции:
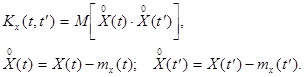
Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящихся к различным 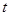 . Положительное значение корреляционной функции свидетельствует о том, что при увеличении (уменьшении) ординат процесса в сечении
. Положительное значение корреляционной функции свидетельствует о том, что при увеличении (уменьшении) ординат процесса в сечении 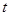 в среднем увеличиваются (уменьшаются) ординаты при
в среднем увеличиваются (уменьшаются) ординаты при 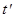 . Отрицательная корреляция означает увеличение (уменьшение) в среднем ординат в сечении
. Отрицательная корреляция означает увеличение (уменьшение) в среднем ординат в сечении 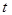 при их уменьшении (увеличении) в сечении
при их уменьшении (увеличении) в сечении 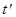 .
.
Корреляционная функция является симметричной функцией своих аргументов, а ее ординаты по абсолютному значению не могут быть больше произведений среднеквадратичных отклонений в моменты времени 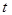 и
и 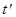 :
:
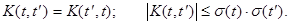
Процесс считается стационарным, если его многомерная плотность распределения не изменяется при сдвиге соответствующих моментов времени на любую величину. В рамках корреляционной теории , процесс считается стационарным, если его ковариационная функция 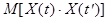 не зависит от времени, а зависит только от разности
не зависит от времени, а зависит только от разности 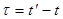 ,
,
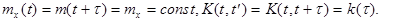
Корреляционная функция стационарного процесса по модулю не превосходит дисперсию:
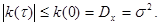
Стационарный процесс у которого корреляционная функция стремится к нулю 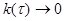 при
при 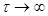 называют эргодичным. Эргодические процессы представляют наибольший интерес для практических приложений, поскольку их характеристики, определяемые по семейству и по одной реализации совпадают:
называют эргодичным. Эргодические процессы представляют наибольший интерес для практических приложений, поскольку их характеристики, определяемые по семейству и по одной реализации совпадают:
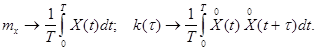
Марковскими случайными процессами называют такие процесса, у которых плотность совместного распределения произвольных двух сечений полностью определяют характер процессов, т.е. дальнейшее поведение процесса зависит только от значений, принятых процессом в настоящий момент времени , и не зависит от ранее принятых.
Марковский случайный процесс, в котором сама функция принимает счетное множество возможных состояний (дискретные состояния) 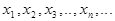 , переход из одного состояния в другое происходит скачком под влиянием случайных факторов, называют цепями Маркова . Если переход из состояния в состояние происходит в дискретные моменты времени
, переход из одного состояния в другое происходит скачком под влиянием случайных факторов, называют цепями Маркова . Если переход из состояния в состояние происходит в дискретные моменты времени 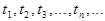 , то такой процесс называют дискретными цепями Маркова. Если переходы возможны в любой момент времени, то процесс называют непрерывными цепями Маркова.
, то такой процесс называют дискретными цепями Маркова. Если переходы возможны в любой момент времени, то процесс называют непрерывными цепями Маркова.
Вероятность того, что дискретная цепь Маркова в момент времени 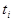 примет значение
примет значение 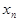 при условии, что в момент времени
при условии, что в момент времени 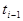 она имела значение
она имела значение 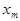 , называют вероятностью перехода из состояние в состояние
, называют вероятностью перехода из состояние в состояние 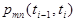 . Если эта вероятность зависит от длины промежутка времени
. Если эта вероятность зависит от длины промежутка времени 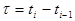 и нет зависит от начала отсчета времени, т.е. не зависит от номера шага, то такую цепь Маркова называют однородной:
и нет зависит от начала отсчета времени, т.е. не зависит от номера шага, то такую цепь Маркова называют однородной: 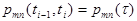 .
.
Дискретные цепи Маркова однозначно определяются либо матрицей переходов
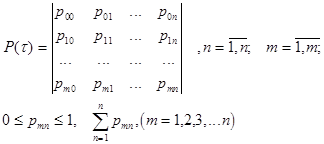
или графом состояний



 Р21 Р32 Р43
Р21 Р32 Р43


 Х1 Х2 Х3 Х4
Х1 Х2 Х3 Х4
 |  |  |
Р12 Р23 Р34
Вектором вероятностей (безусловной вероятностью) состояния цепи Маркова называют вероятности 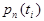 того, что в момент времени
того, что в момент времени 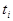 цепь примет значение
цепь примет значение 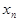 , которая представляет собой матрицу-строку:
, которая представляет собой матрицу-строку:
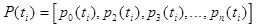 ,
,
где - 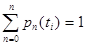 .
.
Вектор вероятностей состояния однородной цепи Маркова после 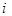 этапов однозначно определяется вектором вероятностей
этапов однозначно определяется вектором вероятностей 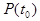 в начальный момент времени матрицей переходов
в начальный момент времени матрицей переходов 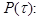
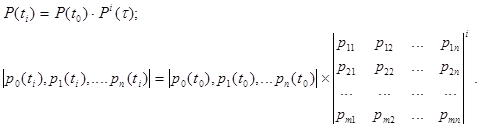
Если в цепи Маркова 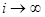 , то вектор вероятностей состояния превращается в вектор финальной (стационарной) вероятности
, то вектор вероятностей состояния превращается в вектор финальной (стационарной) вероятности 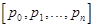 , определяемый из однородной системы n уравнений:
, определяемый из однородной системы n уравнений:
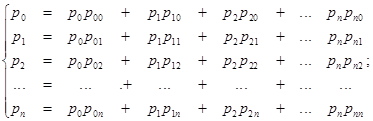
Учитывая, что 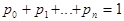 и заменяя этим соотношение одно из вышеприведенных уравнений в системе, находим искомые финальные (стационарные) вероятности однородной цепи Маркова.
и заменяя этим соотношение одно из вышеприведенных уравнений в системе, находим искомые финальные (стационарные) вероятности однородной цепи Маркова.
Для непрерывных цепей Маркова возможности перехода из состояния 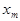 в состояние
в состояние 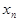 за время
за время 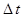 оценивается плотностью вероятностей перехода
оценивается плотностью вероятностей перехода 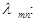
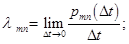 при условии, что
при условии, что 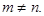
Если 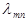 не зависит от времени, то непрерывная цепь Маркова называется однородной.
не зависит от времени, то непрерывная цепь Маркова называется однородной.
Для непрерывных цепей Маркова вектор вероятностей состояния есть функция времени и определяется путем решения системы дифференциальных уравнений, которые составляются по графу состояния цепи Маркова по следующим правилам :
· в левой части каждого уравнения стоят производные по времени вероятностей состояния цепи;
· правая часть этих уравнений содержит столько членов, сколько переходов (стрелок на графе) связанно с данным состоянием;
· каждый член правой части уравнений равен произведению плотности вероятностей перехода , соответствующей данной стрелки графа состояния, умноженной на вероятность того состояния из которого исходит стрелка;
· каждый член правой части уравнений имеет знак «минус», если стрелка графа состояния входит в данное состояния и знак «плюс», если стрелка выходит из данного состояния.
Например: Имеем граф состояния однородной непрерывной цепи ркова:

X1
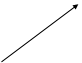
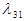
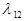


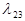
 X3 X2
X3 X2
Для этого графа составляем систему уравнений по вышеуказанным правилам:
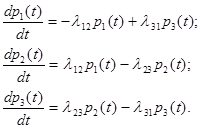
Учитывая, что 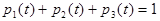 , известными методами находят
, известными методами находят 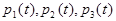 .
.
В случае, когда нас интересую вероятности состояния непрерывных цепей Маркова по истечению длительного промежутка времени (установившейся процесс 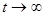 ), то решение системы получают путем записи в левой части системы дифференциальных вместо производных нулей, т.е. :
), то решение системы получают путем записи в левой части системы дифференциальных вместо производных нулей, т.е. :
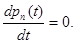
Переход из состояния в состояние в непрерывных цепях Маркова происходит вод воздействием потока событий.
Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.
Поток событий называю простейшим или стационарным Пуассоновским, если он стационарен, ординарен и без последействия.
1. Поток называется стационарным, если вероятность попадания события на участок времени 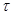 зависит только от длины этого участка и не зависит от места расположения этого участка на оси времени.
зависит только от длины этого участка и не зависит от места расположения этого участка на оси времени.
2. Поток называют потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от числа событий на другом участке.
3. Поток событий называют ординарным, если вероятность попадания на элементарный участок двух и более событий пренебрежительно мала по сравнению с вероятностью попадания на этот участок одного события.
Плотностью вероятностей перехода 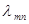 цепи Маркова из состояния
цепи Маркова из состояния 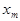 в состояние
в состояние 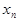 является интенсивностью потока событий
является интенсивностью потока событий 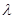 или средним числом событий в единицу времени. Для стационарного потока
или средним числом событий в единицу времени. Для стационарного потока 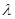 не зависит от времени. Для нестационарного
не зависит от времени. Для нестационарного 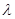 - функция времени
- функция времени 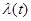 .
.
В Пуассоновском потоке событий число событий, попадающих на любой участок времени 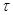 , подчиняется закону распределения Пуассона с математическим ожиданием
, подчиняется закону распределения Пуассона с математическим ожиданием 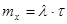 , т.е. вероятность того, что за время
, т.е. вероятность того, что за время  произойдет ровно
произойдет ровно 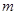 событий, равна:
событий, равна:
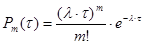 .
.
Промежутки времени 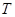 между событиями в Пуассоновском потоке событий подчиняются показательному закону распределения с функцией распределения
между событиями в Пуассоновском потоке событий подчиняются показательному закону распределения с функцией распределения 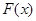 и плотностью распределения
и плотностью распределения 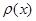 , равные:
, равные:
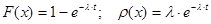 ,
,
с математическим ожиданием 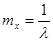 , дисперсией
, дисперсией 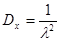 и среднеквадратичным отклонением
и среднеквадратичным отклонением 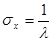 .
.
|
из
5.00
|
Обсуждение в статье: Теорема Чебышева (закон больших чисел). |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

