Лекция №12. Проверка статистических гипотез.

Статистической гипотезой называется любое предположение о виде или параметрах генеральной совокупности, проверяемое по выборке.

Различают простую и сложную статистические гипотезы. Простая гипотеза, в отличие от сложной, полностью определяет теоретическую функцию распределения наблюдаемой случайной величины.

Проверяемую гипотезу обычно называют нулевой . Наряду с нулевой гипотезой  рассматривают альтернативную, или конкурирующую, гипотезу , являющуюся логическим отрицанием .

Правило, по которому принимается или отвергается , называется статистическим критерием.

  Суть проверки статистической гипотезы заключается в том, что используется специальная составленная выборочная характеристика (критерий) 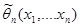, полученная по выборке 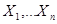, точный или приближенный закон распределения которой при выдвинутой гипотезе известно. По этому распределению определяется критическое значение критерия из условия, что вероятность  мала. Так что в соответствие с принципом практической уверенности в условиях данного исследования при правильности гипотезы  событие практически невозможно. Таким образом, множества значений критерия разбивается значением  на два непересекающихся подмножества:

· Область допустимых значений  (область принятия гипотезы , когда );

· Критическая область  (область отбрасывания гипотезы , когда ).

При таком подходе возможны четыре случая (см. табл.):

Гипотеза	Принимается	Отвергается
Верна	Правильное решение	Ошибка 1-го рода
Неверна	Ошибка 2-го рода	Правильное решение

Таким образом, вероятность , называемая уровнем значимости критерия, есть вероятность допущения ошибки 1-ого рода.

Вероятность допустить ошибку 2-ого рода обозначают . Вероятность недопущения ошибки 2-ого рода  называется мощностью критерия.

При фиксированном объеме выборке невозможно одновременное уменьшение ошибок 1-ого и 2-ого рода. Критическая область следует выбирать так, чтобы при заданном уроне значимости  мощность критерия  была максимальной. Вид критической области зависит от конкурирующей гипотезы и бывает трех видом:

· Правосторонняя, выбирается из соотношения:               ;

· Левосторонняя: ;

· Двухсторонняя: .

Критерии проверки гипотез называю параметрическими, если известен закон распределения генеральной совокупности, что задает определенное распределение критерия. При неизвестном законе распределения генеральной совокупности, то критерии называют непараметрическими.

По своему прикладному содержанию. Статистические гипотезы подразделяются на несколько основных типов:

· О равенстве числовых характеристики генеральных совокупностей;

· О числовых значениях параметров;

· О законе распределения;

· Об однородности выборок (т.е. о принадлежности их одной и той же генеральной совокупности).