Методы решения задач управления

 

Классические методы высшей математики используются в таких традиционных экономических расчетах как обоснование потребности в ресурсах; определение множества плановых и фактических технико-экономических показателей; оценка деятельности и эффективности производства; выполнение некоторых оптимизационных расчетов и др.

Следует подчеркнуть, что методы классической высшей математики применяются в рамках практически всех экономико-математических методов.

Методы теории вероятностей и математической статистики. На процесс принятия управленческих решений как на макро-, так и на микроуровне в условиях рынка влияет множество случайных факторов, имеющих вероятностный характер. Поэтому методы теории вероятностей и математической статистики занимают приоритетное место среди всех остальных по частоте и широте использования их в задачах управления.

При решении задач управления предприятием наиболее часто используются следующие методы математической статистики: корреляционно-регрессионный анализ; дисперсионный анализ; факторный анализ; кластерный анализ; дискриминантный анализ.

Методы теории вероятностей и математической статистики позволяют определить: значения вероятностей наступления определенных событий; математического ожидания той или иной случайной величины; установить статистические закономерности изменения выходных параметров того или иного производственного процесса от действия случайных факторов; установить тесноту взаимосвязи отдельных случайных факторов; определить факторы, существенно влияющие на выходную величину и др.

Статистика совместно с современными информационными технологиями позволяет достаточно оперативно отражать состояние рынка, охарактеризовать его структуру и динамику, оценить его колебания, выявить и смоделировать влияние рыночных факторов, сделать обоснованные выводы, построить прогнозы, определить надежность достижения поставленных целей и оценить возможный риск [5].

В математике существуют два понятия, отражающих причинно-следственные связи: функциональная и корреляционная зависимость.

Под функциональной зависимостью подразумевается такая связь между величинами, когда значение зависимой величины-функции полностью определяется значением других переменных величин-аргументов.

Корреляционная зависимость имеет место, когда каждому значению одной величины соответствует множество случайных значений другой, возникающих с определенной вероятностью. При корреляционной связи изменение одной величины вызывает изменение среднего значения другой величины.

В процессе изучения экономических явлений чаще всего мы имеем дело не с функциональными, а с корреляционными зависимостями. При парной корреляции наблюдается связь между двумя величинами. При множественной корреляции определенным значениям нескольких влияющих величин-факторов соответствует множество случайных значений зависимой результатной величины, распределенных по известному закону. Вместе с тем можно подобрать некоторую функцию, которая приближенно (в среднем) будет отражать зависимость результатной величины от вышеуказанных факторов. Такая функция называется уравнением регрессии, а ее график - линией регрессии. Корреляция и уравнение регрессии могут быть линейными или нелинейными.

С помощью корреляционно-регрессионного анализа можно моделировать и прогнозировать функции спроса [3, 6]; функции потребления [3]; планировать расходы на рекламу и оценивать ее эффективность [7]. Для оценки эффективности сегментирования рынка используется дисперсионный анализ [8, 9, 10]. На элементах теории вероятности и нечеткой логики можно осуществить оценку факторов риска при поиске целевых рынков [11].

Методы теории вероятностей и математической статистики являются базовыми для разработки методовстатистической теории принятия решений (теория игр, теория массового обслуживания, стохастическое программирование), которая используется для описания реакции покупателей на конъюнктурные сдвиги, обоснования стратегии маркетинга, выбора наиболее эффективных коммерческих решений, оптимизации систем обслуживания и других задач управления предприятием.

Оптимизационные методы позволяют из множества допустимых решений выбрать оптимальное в соответствии с критерием оптимальности. Выбор критерия оптимальности при решении управленческих задач является не простым шагом в силу его неоднозначности. Экономисты, как правило, предлагают принять в качестве главного критерия оптимальности один из следующих показателей: а) максимум реализации продукции; б) минимум оборотных средств, вложенных в совокупные запасы у изготовителей продукции, находящейся в пути, на снабженческо-сбытовых складах и у потребителей; в) полнота удовлетворения потребностей народного хозяйства в продукции; г) максимум прибыли; д) минимум приведенных совокупных затрат; е) производительность живого труда; е) минимум транспортных расходов и т. д. [12].

Оптимизационные методы математического программирования позволяют исследовать и решить ряд важнейших управленческих задач. В самом общем случае детерминированная задача математического программирования состоит в нахождении максимума или минимума целевой функции

                  

                   (2.1)

 

при условии, что переменные удовлетворяют соотношениям

 

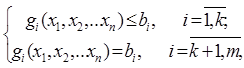                                             (2.2)

                       ,                              (2.3)

 

где q и g_i – некоторые известные функции n переменных;

b_i - заданные числа.

Методы линейного программирования (ЛП). Задачи линейного программирования характерны тем, что целевая функция q ( x ) задачи (2.1)- (2.3) представляет собой линейную зависимость от координат вектора х, а ограничения g_i ( x ) либо линейные уравнения, либо линейные неравенства. Методы ЛП рассмотрены в работах [3, 12-16].

Каждая из задач ЛП является частным случаем общей задачи ЛП, математическая модель которой состоит из целевой функции

 

                                        (2.4)

 

и системы ограничений

 

                                      (2.5)

 

где а _ij , b_i , c_j – заданные постоянные величины и k £ m .

Различают еще две основные формы задач ЛП в зависимости от наличия ограничений разного типа: стандартная иканоническая.

Стандартная форма модели интересна тем, что большое число прикладных моделей естественным образом сводится к этому виду моделей.

Каноническая форма модели важна ввиду того, что основные вычислительные схемы различных вариантов симплекс-метода разработаны именно для этой формы.

Указанные выше задачи ЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть приведена к любой из двух остальных. Следовательно, любую задачу ЛП можно привести к каноническому виду. Поэтому умение решать задачу в канонической форме позволяет решать задачу и в любой другой форме.

 Методы линейного программирования применяются при решении таких задач управления, как определение выгодного ассортимента при ограниченных ресурсах; определение оптимального расположения складов; расчет оптимальной величины товарных запасов; планирование маршрутов движения сбытовых агентов; планирование производства и др. Они также используются при организации хозяйственных оптимальных связей между поставщиками и потребителями. В этом случае критерий оптимальности - минимизация транспортных расходов.

В таблице 2.3 приведен список оптимизационных задач управления предприятием, которые могут быть решены методами ЛП.

 

Таблица 2.3 – Список оптимизационных задач управления предприятием,

которые могут быть решены методами ЛП

№ п/п	Оптимизационные задачи управления предприятием, решаемые методами ЛП	Примечания
1	Задачи технико-экономического (производственного) планирования	Детерминированная, статическая
2	Задача максимизации выпуска комплектной продукции	-||-
3	Задача максимизации изготовляемой комплектной продукции с учетом возможности цехов	-||-
4	Задача загрузки невзаимозаменяемых групп оборудования	-||-
5	Задача загрузки взаимозаменяемых групп оборудования	-||-
6	Задачи оптимальных смесей	-||-
7	Задачи оптимального раскроя материалов для получения заданного количества заготовок	-||-
8	Задачи оптимального раскроя партий материалов для изготовления комплектов	Детерминированная, статическая. Сводится к задаче ЛП.
9	Задача объемно-календарного планирования в крупносерийном производстве	Детерминированная, статическая.
10	Задача определения последовательности запуска деталей	Детерминированная, статическая. Сводится к задаче ЛП.
11	Закрытая и открытая транспортные задачи	Детерминированная, статическая.
12	Многоэтапные транспортные задачи	-||-
13	Задачи об оптимальных назначениях	Детерминированная, статическая. Частный случай транспортной задачи.
14	Задачи о спросе и предложении	Детерминированная, статическая.
15	Задача оптимизации прикрепления потребителей к поставщикам	-||-
16	Задача о размещении складов	При некоторых условиях сводится к транспортной задаче.

 

Методы линейного целочисленного программирования (ЛЦП). По смыслу значительной части экономических задач, относящихся к задачам ЛП, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. Например, к этим задачам относятся задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования и многие другие. Методы ЛЦП рассмотрены в работах [12-14].

Оптимизационные модели ЛЦП используются при решении в основном таких задач, как рациональное распределение материальных ресурсов, получение наиболее выгодного ассортимента при ограниченных ресурсах, получение оптимального состава компонентов, оптимального раскроя материалов. В задаче о наилучшем выборе предметов из общего количества (задача о ранце) требуется, чтобы вес или объем выбранных предметов не превышал требуемой величины, а общая их полезность была максимальной. Она актуальна при оптимизации заполнения складов, транспортных средств и др.

Следует отметить, что классическая транспортная задача и некоторые другие задачи транспортного типа "автоматически" обеспечивают решение задачи в целых числах (если, конечно, целочисленны параметры условий). Однако в общем случае условие целочисленности, добавляемое к обычным задачам ЛП, существенно усложняет ее решение.

Для решения задач ЛЦП используется ряд методов. Самый простой из них - обычный метод ЛП. Присущие целочисленному программированию трудности вычислительного характера иногда пытаются обойти округлением решения, полученного без учета целочисленности. Округление в данном случае есть не что иное, как приближение. При этом округленное решение должно удовлетворять ограничениям задачи. Но такой подход не имеет обоснования, поэтому округление нельзя рекомендовать как метод.

Одна из основных трудностей, свойственная задачам ЛЦП, заключается в том, что нет простого способа, позволяющего определить, является ли данное допустимое решение оптимальным. Методы целочисленной оптимизации можно разделить на три основные группы: а) методы отсечения; б) комбинаторные методы; в) приближенные методы. В общем виде задача ЛЦП формулируется так же, как и задача ЛП (2.4)-(2.5), но включает дополнительное требование, состоящее в том, что значения переменных x_j оптимального решения должны быть целыми числами.

Для решения задач ЛЦП разработаны специальные методы. Метод отсекающих плоскостей разработан Р. Гомори и применяется для решения задач ЛЦП, в которых все переменные целочисленны. Как показала практика, ни один из вариантов метода отсекающих плоскостей не обеспечивает высокой эффективности вычислительных процедур для решения задач большой размерности [14]. Метод ветвей и границ относится к комбинаторным методам и в отличие от методов отсекающих плоскостей непосредственно применим как к полностью, так и к частично целочисленным задачам. Он достаточно эффективен лишь в том случае, когда используемый конкретный алгоритм учитывает специфику решаемой задачи [14].

В таблице 2.4 приведен список оптимизационных задач управления предприятием, которые могут быть решены методами ЛЦП.

 

Таблица 2.4 – Список оптимизационных задач управления предприятием,

которые могут быть решены методами ЛЦП

№ п/п	Оптимизационные задачи управления предприятием, решаемые методами ЛЦП	ПРИМЕЧАНИЕ
1	Задача распределения производственной программы во времени	Детерминированная, статическая.
2	Задача определения последовательности запуска деталей с учетом переналадки	-||-
3	Некоторые задачи транспортного типа (об оптимальных назначениях, о кратчайшем пути)	-||-
4	Задача о коммивояжере	-||-
5	Задача оптимального раскроя промышленных материалов	-||-
6	Задача о ранце	-||-

 

Методы динамического программирования (ДП). Динамическое программирование – это поэтапное планирование многошагового процесса, когда на каждом этапе оптимизируется только один шаг, но решение, под воздействием которого система переходит из текущего состояния в новое состояние, должно выбираться с учетом его последствий в будущем и совершенно не обязательно должно давать наибольший эффект на данном этапе. Начало развития методов ДП связано с именем Р. Беллмана. Методы ДП рассмотрены в работах [13, 14, 16, 17].

В управлении методы ДП применяются при решении следующих задач: разработка правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; распределение дефицитных капитальных вложений между возможными новыми направлениями их использования и т. п. [13].

В научной литературе одна часть авторов [13] считает класс моделей ДП составляющей частью класса моделей нелинейного программирования (НП), другая часть выделяет класс моделей ДП в самостоятельный класс в составе класса моделей математического программирования. Многие задачи управления предприятием можно рассматривать как процесс принятия решения, причем эти решения принимаются в определенной последовательности (упорядоченный перебор вариантов), что делает данный процесс многошаговым. Попытки решения такого типа задач классическими методами вычисления экстремумов функций многих переменных из-за значительного количества входных параметров, определяющих решение задачи, в большинстве случаев оказываются безрезультатными.

На первый взгляд задача может показаться весьма тривиальной, необходимо лишь разбить многошаговый процесс на отдельные шаги, изучить состояние системы и выбрать для каждого шага оптимальное решение. Однако управление, оптимальное для какого-либо отдельного шага, может помешать получить оптимальное решение для всего процесса в целом. Метод динамического программирования и заключается в том, что оптимальное управление строится постепенно - на каждом этапе управления выбирается оптимальное решение не для данного шага, а для всего процесса в целом.

Это основное правило сформулировано Р. Беллманом в виде такого принципа оптимальности: каково бы ни было предшествующее состояние системы, последующие решения должны выбираться оптимальными относительно состояния, к которому придет система в конце предыдущего шага.

Принцип оптимальности, положенный в основу динамического программирования, предполагает построение своеобразных функциональных уравнений, решение которых возможно средствами вычислительной математики.Этопозволяет на основе стандартного подхода принимать весьма значительное (с применением ЭВМ) количество решений, совокупность которых определяет правила управления запасами, распределения ограниченных ресурсов, порядок обновления выбывающих основных фондов и др.

Общие свойства динамических моделей сводятся к следующему:

- цель программирования (принцип решений) - максимизация некоторой функции параметров состояния;

- состояние системы в любой момент времени характеризуется небольшим количеством параметров;

- результатом принятия решения является преобразование этих параметров в том же количестве, но с другими числовыми значениями;

- поведение системы в будущем определяется ее состоянием в данный момент времени и очередными шагами и не зависит от предыстории процесса, т.е. от того, в каких состояниях система находилась до этого момента времени.

Из общего правила, сформулированного Р. Беллманом, есть одно исключение - на последнем шаге процесса, на котором нет будущего, решение можно принимать оптимальным только для данного шага. Поэтому в большинстве случаев процесс динамического программирования начинается с планирования последнего шага. Причем делаются различные предположения о том, чем кончился предпоследний шаг, и для каждого из них выбирается управление, максимизирующее выигрыш (доход, экономический эффект от принятого решения) на последнем шаге. Руководствуясь таким принципом и осуществляя процесс решения с конца, находим оптимальное управление для первого шага, т. е. для начала процесса. Очевидно, если принято правильное решение на первом шаге и учтены его последствия в дальнейшем, можно быть уверенным, что данные решения оптимальны для всего процесса в целом. Этим завершаются основные вычисления для динамических моделей, называемые условной оптимизацией. Следующий этап - безусловная оптимизация.

 

Рисунок 2.2 – Экономико-математические методы решения

оптимизационных задач

 

Предположим, что в результате условной оптимизации стали известны начальное состояние системы S_o и оптимальное управление Х(Х₁, Х₂,..., Х _n ),переводящее систему в состояние S ₁ , затем - в S ₅ и т. д. до получения максимального выигрыша f_n ( S ). Из этого следует, что в результате безусловной оптимизации определяются оптимальные управления на всех шагах процесса, приводящие к максимально возможному выигрышу Z_max.

Таким образом, динамическое программирование предполагает осуществление пошагового процесса оптимизации дважды:

- от конца к началу, в результате чего находятся условно-оптимальные управляющие воздействия;

- от начала к концу, в результате чего определяются оптимальные шаговые управления на всех стадиях процесса.

Для решения задач динамического программирования существует рекуррентная вычислительная схема, называемая уравнением Беллмана.

В таблице 2.5 приведен список оптимизационных задач управления предприятием, которые могут быть решены методами ДП.

 

Таблица 2.5 – Список оптимизационных задач управления предприятием,

которые могут быть решены методами ДП

№ п/п	Оптимизационные задачи управления предприятием, решаемые методами ДП	ПРИМЕЧАНИЕ
1	Задача оптимальной замены оборудования	Динамическая, детерминированная
2	Задача управления запасами предприятия	-||-
3	Задача распределения ограниченных ресурсов	-||-
4	Задача о загрузке транспортных средств	-||-

 

Методы нелинейного программирования (НП). Нелинейное программирование – раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых и (или) целевая функция (2.1) нелинейная, и (или) система ограничений (2.2) нелинейная. Если в задаче (2.1)-(2.3) x_i ³0 i =1,… n , а функция q – выпуклая и область допустимых решений, определяемая ограничениями (2.2), тоже выпуклая, то для этого случая разработаны эффективные методы решения (выпуклое и квадратическое программирование).Методы НП рассмотрены в работах [1, 13, 14, 17].

В управлении предприятием НП применяется при решении задач планирования производства, прогнозирования, управления товарными ресурсами, контроля качества выпускаемой продукции и др. С помощью методов нелинейного программирования решается задача планирования производства для предприятия-монополиста на рынке продукции [18], а также задача формирования планов выпуска продукции с учетом обобщенных стоимостных оценок параметров объектов в системе управления ресурсами [19, 20].

Экономико-математические модели НП характерны тем, что для их решения не существует универсального метода. Для каждой конкретной задачи вопрос о том, какие характеристики следует выбирать для вычисления, решается в зависимости от свойств минимизируемой функции, ограничений и имеющихся возможностей по хранению и обработке информации на ЭВМ.

Задачи выпуклого программирования (ВП) являются задачами нелинейного программирования. Методы ВП используются при решении оптимизационных задач в маркетинге. Выделение задач ВП в специальный класс объясняется экстремальными свойствами выпуклых функций:

- всякий локальный минимум выпуклой функции (локальный максимум вогнутой функции) является одновременно и глобальным;

- выпуклая (вогнутая) функция, заданная на замкнутом ограниченном множестве, достигает на этом множестве глобального максимума и глобального минимума.

Квадратическое программирование, как и выпуклое программирование, является также частным случаем НП и характерно тем, что в задаче минимизируется сумма линейной и квадратичной форм при ограничениях вида линейных неравенств и неотрицательности переменных. Для данной задачи, как и вообще для задачи НП, эффективный вычислительный метод можно найти только в том случае, если целевая функция имеет единственный оптимум, который и является глобальным.

Если все ограничения в (2.2) являются строгими равенствами, то задачу (2.1)-(2.3) называют классической задачей оптимизации. Ее решают с помощью множителей и функции Лагранжа. Иногда удается, опираясь на условия оптимальности или на геометрическую интерпретацию, получить решение задачи (2.1)-(2.3) в явном виде, но в большинстве случаев задачу приходится решать численно с применением ЭВМ.

При решении безусловных нелинейных оптимизационных задач применяются следующие численные методы:

- методы прямого поиска (метод конфигураций, метод деформируемого симплекса). Основное достоинство методов прямого поиска состоит в том, что они не требуют непрерывности целевой функции и существования производных;

- градиентный метод. В общем случае градиентный метод позволяет найти точку локального экстремума. В моделях ВП он определяет глобальный экстремум. Этот метод имеет один недостаток – чувствительность к погрешностям вычислений. Поэтому градиентный метод в начальной стадии поиска работает лучше, чем на его заключительном этапе;

- метод Ньютона. Сам метод и его модификации относятся к числу наиболее эффективных способов решения задач оптимизации;

- квазиньютоновский метод – модификация метода Ньютона.

При решении нелинейных оптимизационных задач с ограничениями (2.2) применяются следующие численные методы:

- метод кусочно-линейной аппроксимации нелинейной модели с последующим применением методов линейного программирования;

- метод скользящего допуска, который позволяет улучшить значение целевой функции. Метод скользящего допуска использует алгоритмы метода прямого поиска;

- метод, связанный с построением функции Лагранжа и последующим применением одного из численных методов безусловной оптимизации;

- методы штрафных функций. Идея методов штрафных функций состоит в том, что во всех этих методах осуществляется преобразование задачи нелинейного программирования при наличии ограничений либо в одну эквивалентную задачу без ограничении, либо в эквивалентную последовательность задач без ограничений. Методы штрафных функций в сочетании с методами поиска безусловного экстремума являются универсальным средством решения задач математического программирования. К методам штрафных функций относится целая группа методов, связанных с параметризацией исходной задачи. Один из самых распространенных подходов основан на введении функций штрафа,зависящих от штрафного параметра.

В таблице 2.6 приведен список оптимизационных задач управления предприятием, которые могут быть решены методами НП (в частности квадратического программирования и ВП).

       

Таблица 2.6 – Список оптимизационных задач управления предприятием,

которые могут быть решены методами НП

№ п/п	Оптимизационные задачи управления предприятием, решаемые методами НП	ПРИМЕЧАНИЕ
1	Задача распределения оборудования по видам работ	Детерминированная, статическая
2	Задача распределения оборудования по местам	Детерминированная, статическая. Является квадратической задачей о накоплениях
3	Задача о переналадках	Детерминированная, статическая
4	Задача прогнозирования совокупности экономических показателей с учетом взаимозаменяемости	-||-
5	Задача размещения баз снабжения	-||-
6	Задачи моделирующие поведение производителя, основанное на максимизации прибыли	Детерминированная, статическая
7	Задачи моделирующие поведение фирм на конкурентных рынках.	-||-
8	Задача планирования производства для предприятия-монополиста на рынке продукции	-||-
9	Задача формирования планов выпуска продукции с учетом обобщенных стоимостных оценок параметров объектов в системе управления ресурсами	-||-

 

Методы стохастического программирования (стохастической оптимизации). Чаще всего изучаемая система, источники которой имеют разнообразную природу, функционирует в случайных условиях. На нее могут влиять внешние возмущающие силы, которые либо неизвестны, либо имеют весьма сложный характер, и их точный учет затруднен. Управлению предприятием в условиях рынка присущи неполнота и неопределенность информации, невозможность точного предсказания. Случайный фактор обусловлен, например, неустойчивостью спроса на готовую продукцию, а также случайными условиями реализации производственной программы. Модели, учитывающие случайный характер исходной информации, сводятся к стохастическим моделям, которые делятся на два класса: модели в условиях риска и модели в условиях неопределенности. Модели в условиях риска содержат случайные факторы, распределения которых известны. Модели в условиях неопределенности включают факторы с неизвестными законами распределения или с недостаточной информацией о них. Например, непредсказуемость возникает, когда увеличивается доля новых товаров, а спрос на них на рынке не изучен. Методы стохастического программирования рассмотрены в работах [21-23].

Задача стохастического программирования состоит в нахождении детерминированного вектора 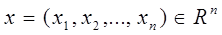, при котором максимизируется математическое ожидание:

 

,        (2.6)

при ограничениях:

 

, i=1,2,....,m ,                (2.7)

 

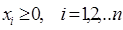,                                            (2.8)

 

где - вектор, принадлежащий пространству случайных неуправляемых параметров .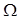

Целевую функцию F ⁰ ( x ),определенную в (2.6), называют функцией риска..

Наличие стохастической неопределенности вносит в процесс принятия управленческих решений в экономике элемент риска. Поэтому стохастические задачи, в том числе и оптимизационные, иногда называют задачами в условиях риска. Управленческие решения, принятые на базе решения таких задач, называют решениями, принятыми в условиях риска. В зависимости от конкретного вида f (х, w ) и природы параметров в рамках задачи (2.6)-(2.8) можно решать как статические, так и динамические одно-, двух- и многоэтапные задачи стохастического программирования.

В одноэтапных задачах управленческое решение, принимаемое на основе статистическихданных о фактических значениях случайных параметров, остается неизменным после принятия решения. Такой подход может привести к тому, что в результате наступления неучтенной реализации случайных параметров модели первоначально принятый уровень производства окажется неудачным. Необходимость учета возможной корректировки уровня производства в условиях неопределенности и риска приводит к рассмотрению двухэтапных моделей управления производством.

В двухэтапных моделях первоначально принятое (на основе имеющихся статистических данных) решение в условиях недостоверности информации о случайных факторах впоследствии уточняется, корректируется по мере получения все более точной информации о них. При этом принимаемое решение должно быть устойчивым по отношению к изменениям исходных данных. Количество этапов уточнения решения определяется прежде всего тем, сколько раз можно получить все более точную информацию о случайных параметрах (один, два, три и т.д). В этом случае окончательное решение принимается с помощью двухэтапных (многоэтапных) задач стохастического программирования.

Таким образом, основной целью двухэтапных задач является выбор решения, минимизирующего ожидаемые затраты на его реализацию и коррекцию. Корректировка уровня производства не является следствием недостатков производственно-экономической системы, она органически присуща управлению производством в условиях риска и неопределенности. Коррекция вызвана необходимостью компенсации неувязок – несоответствия между случайными параметрами и выходной величиной.

При решении задачи (2.6)-(2.8) появляется ряд трудностей, состоящих в том, что при фиксированном х вычисление F⁰(х) требует значительных усилий, так как это связано с вычислением многократных интегралов, а также учетом ограничений (2.7), особенно когда они образованы ограничениями стохастического характера. Более того, обычно при решении практических задач вместо значений F ⁰ (х) имеется возможность наблюдать значения функции f (х, w ) при фиксированных х и w. Поэтому в задаче (2.6)-(2.8) нельзя широко применять методы классического анализа и нелинейного программирования. Для решения таких задач развиваются специальные стохастические методы. Исходя из особенности задач, методы их решения обычно делятся на две группы: прямые и непрямые.

В непрямых методах стремятся вычислить F⁰ (х) и свестизадачу(2.6)-(2.8) к задаче, которую можно решить известнымиметодамиклассического анализа и нелинейного программирования.Инымисловами, вместо стохастической задачи рассматривается ее детерминированный аналог. Поэтому успех применения непрямыхметодов в значительной степени зависит от вероятностных свойствw  исвойствфункций, входящих в решаемую задачу.

В зависимости от того, сводится ли стохастическая задача (2.6)-(2.8) к эквивалентной ей задаче или к задаче, решение которой в некотором смысле близко к исходной, непрямые методы подразделяются на точные и приближенные. Как точные, так и приближенные непрямые методы решения стохастических задач управления производством могут быть основаны на применении необходимых и достаточных условий экстремума, на параметризации решения или приближенной замене закона распределения случайного параметра, на использовании детерминированного аналога стохастической модели.

Непрямые методы, как правило, дают неплохие результаты на узком классе задач, специфику которых они учитывают. Применение классического анализа возможно для решения задач малой размерности в случае, когда известна функция распределения φ( w ) случайных параметров w,причем, когда необходимо отыскать безусловный максимум или минимум функции F ⁰ ( x ). Его применение для решения стохастических задач наталкивается на следующие трудности.

Во-первых, не во всех прикладных задачах возможно точное построение функции j ( w ). В ряде задач, например, когда w представляет собой функцию первично наблюдаемых случайных параметров, такое построение практически невозможно. Иногда препятствием для построения j ( w ) является малый объем статистической выборки.

Во-вторых, целевая функция (2.6) в общем случае негладкая. Указанные трудности сужают область применения классического анализа.

Прямые методы позволяют решать задачу (2.6)-(2.8) в условиях, когда функции распределения случайного параметра w неизвестны, но существует способ вычисления случайной функции f (х, w ) на основе имеющейся информации относительно этого параметра. Эти же методы применимы и тогда, когда вероятностные свойства w заданы, но вычисления функции F⁰(х) либо невозможны, либо слишком сложны. Это бывает обусловлено сложностью зависимости функции f (х, w ) от ее параметров х и w, или когда эта функция задается алгоритмически - с помощью имитационной модели.

Известны следующие прямые стохастические методы: методы случайного поиска [24]; методы стохастической аппроксимации [23]; методы стохастических квазиградиентов с проектированием и стохастической линеаризации [22]. В управлении стохастические методы используются для решения задач: управления запасами и производством при случайном спросе; определения оптимального количества продукции, транспортируемой потребителю; управления производством сезонного товара; определения объема заказа полуфабрикатов и др. [22].

В методах случайного поиска существенно используется информация о точных значениях минимизируемых функций, поэтому они применимы только для задач нелинейного программирования. Примером применения этого метода могут быть работы [19, 20], в которых решена задача формирования производственной программы предприятия.

Методом стохастической аппроксимации решается простейшая задача стохастического программирования, занимающая в общих постановках такое же место, как и классическая задача на безусловный экстремум в нелинейном программировании, - отсутствуют ограничения, функция цели имеет ограниченные вторые производные [23].

Методы стохастических квазиградиентов с проектированием и стохастической линеаризации в некотором смысле объединяют идеи указанных выш