 |
Главная |
Элементарные графы ортогональных поворотов
|
из
5.00
|
Матрицы направляющих косинусов единичных ортогональных соответствуют следующие выражения, которых всего три:
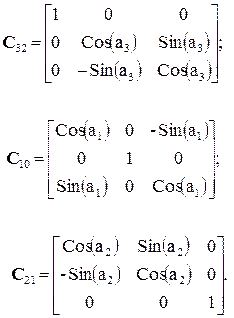 (1.22)
(1.22)
Вид этих матриц можно определить из следующего подхода. Запишем соотношение (1.7) в развернутом виде
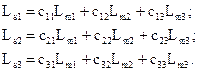 (1.23)
(1.23)
Полученные формулы можно рассматривать как результат прохождения по некоторой ветке графа, где направляющие косинусы  – есть масштабные коэффициенты соответствующих ветвей (ребер) графа.
– есть масштабные коэффициенты соответствующих ветвей (ребер) графа.
Поскольку речь идет о преобразовании трехмерного пространства, то в качестве элементарных графов (граф-схем), отображающих взаимосвязь между системами координат при повороте только относительно одной оси, – соответствуют три схемы (см. Рис.1.3.):

Рис.1.6. Граф-схема ортогонального поворота относительно 1-ой оси

Рис.1.7. Граф-схема ортогонального поворота относительно 2-ой оси

Рис.1.8. Граф-схема ортогонального поворота относительно 3-ей оси
Каждая из схем соответствует элементарному повороту системы координат относительно только одной оси X, Y или Z. Т.к. в разных ситуациях оси могут быть обозначены разными буквами (или наборами букв) условимся обозначать оси цифрами 1, 2, 3, которые соответствуют элементарному повороту относительно первой, второй или третьей оси системы координат. На Рис.1.6. показана схема графов, соответствующая трем последовательным поворотам, которые условно обозначим (231).
Пусть этот пример имеет непосредственное отношение к ориентации самолета относительно географической системы координат. Т.е. УОП в этом примере есть: -Ψ (угол курса), J (угол тангажа) и γ (угол крена). Матрица направляющих косинусов примет вид:
 ;
;
где

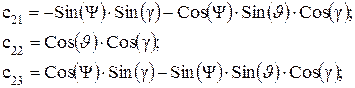 (1.24)
(1.24)

Правильность полученных выражений можно проверить по граф-схеме (рис.1.6.). Для этого мысленно поместим единичный вектор на соответствующую ось (например, X0) и найдем путь (или пути) перехода по графу к нужной оси (например, Y3). При этом перемножаем коэффициенты, расположенные на ребрах графа, по которым мысленно проходим к конечному пункту. В данном варианте имеем.
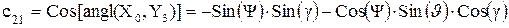
Очевидно, возможны два основных направления ортогональных поворотов:
· переход в направлении 1→2→3→1→ и т.д. (условно назовем – "по ходу часовой стрелки");
· переход в направлении 1→3→2→1→ и т.д. (условно назовем – "против хода часовой стрелки").
Тогда, учитывая четыре группы углов ортогональных поворотов, используя составленные таблицы, можно путем замены обозначений осей и углов получать необходимые таблицы без дополнительных построений и вычислений.
Т.к. минимальное количество независимых параметров, определяющих угловую ориентацию ПО, равно трем; а количество направляющих косинусов девять, то из этого следует:
· направляющие косинусы не являются обобщенными координатами;
· условия масштабирования и условия ортогональности являются дополнительными условиями, устанавливающих связь между направляющими косинусами: 9-3-3=3 – количество независимых параметров, определяющих угловую ориентацию ПО.
Отмеченная особенность направляющих косинусов создает в ряде случаев их использования вычислительные трудности, что приводит к необходимости искать обходные пути:
· использовать направляющие косинусы совместно с углами ортогональных поворотов;
· использовать другие параметры, задающих угловую ориентацию ПО, например, кватернионы.


Рис.1.9. Граф-схема последовательностей поворотов 231;
здесь: S – sin(…); C – cos(…).
Кватернионы
|
из
5.00
|
Обсуждение в статье: Элементарные графы ортогональных поворотов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

