Задание положения используемых систем координат

Зададим положение точки P в системе координат СК_m, заданное в однородных координатах вектором ; здесь нижний индекс указывает на принадлежность к точке М, или оси x, y или z; верхний индекс указывает на принадлежность к системе координат. Определим положение этой точки P в неподвижной системе координат СК_s, для чего используем следующее соотношение

. (4.4)

Здесь - однородная матрица перемещения, характеризующая местоположение и ориентацию системы координат СК_m относительно системы СК_s и состоящую из однородной матрицы поворота и однородной матрицы переноса

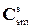: . (4.5)

Рассмотрим пример использования однородных координат в задаче движения центра масс ЛА относительно поверхности Земли.

Построим кинематическую схему связи между следующими системами координат:

· М X_gY_gZ_g – географическая система координат, установленная в месте положения ЛА, (на Рис. обозначенного на рисунке точкой М);

· О_GX_GY_GZ_G – геоцентрическая инерциальная система координат: центр системы координат находится в центре масс Земли; ось Y_G образована пересечением плоскостей экватора и Гринвичского меридиана, ось X_G направлена по оси вращения Земли в сторону северного полюса; вспомогательная ось Y' образована пересечением плоскостей экватора и меридиана, проходящего через место положения ПО. Эта система неподвижна относительно инерциального пространства, а ее начальное положение определяется моментом начала движения ЛА, в который она как бы "замирает/останавливается" относительно инерциального пространства.

· О_сX_сY_сZ_с – связанная (с ЛА) система координат;

· О_iX_iY_iZ_i - установочная система координат; система координат в которой

устанавливаются измерительные устройства на борту ЛА.

Введем в рассмотрение следующие параметры:

· l, j - географическая долгота и географическая широта места точки М начала географическая система координат соответственно,

· R_з – радиус Земли, h – высота полета ЛА;

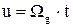· - угол поворота Земли за время рассмотрения движения ЛА; - вектор угловой скорости Земли

· - углы ориентации ЛА относительно географической системы координат;

· - углы ориентации установочной системы координат относительно связанной системы координат ЛА;

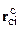· - вектор положения начала установочной системы координат относительно связанной в проекциях на связанную систему координат.

Кинематическая схема связи между введенными системами координат имеет вид

В соответствии с кинематической схемой связи между системами координат можем записать следующие соотношения:

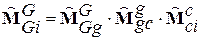. (4.6)

Здесь

; ; ; (4.7)

Где

; ; ; (4.8)

, ;

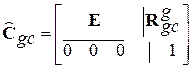; (4.9)

; . (4.10)

(4.11)

Матрица направляющих косинусов 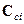может быть выражена через углы , если задать принятую последовательность поворотов на эти углы.

Производя перемножение матриц в соответствии с уравнением (6) и учитывая соотношения (7) …(11), находим компоненты матрицы 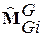, т.е. ориентацию и положение установочной системы координат относительно инерциальной системы отсчета в виде матриц и . Следовательно, компоненты матриц и определяют абсолютные угловые и линейные координаты установочной системы координат, т.е. определяют параметры движения измерительных устройств, установленных на борту ЛА и совершающие вместе с ним движение.