Доказать, что квадратичная форма А положительно или отрицательно определенная

Решение:

Квадратичной формой от n переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом.

1) Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. а₁₁=1, а₂₂=0, а₃₃=1, а другие элементы – половинам соответствующих коэффициентов квадратичной формы, т.о., а₁₂=а₂₁, 2а₁₂ = -3, а₁₂=а₂₁=-1,5; а₁₃=а₃₁, 2а₁₃=4, а₁₃=а₃₁=2; а₂₃=а₃₂, 2а₂₃=2, а₂₃=а₃₂=1. Следовательно, матрица А квадратичной формы имеет вид:

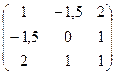
2) Приведем квадратичную форму к каноническому виду. Вначале выделим полный квадрат при переменной х₁, коэффициент при квадрате которой отличен от нуля:

.

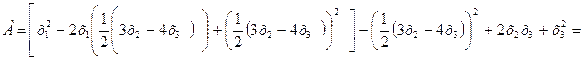
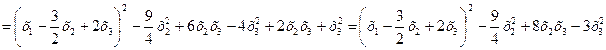Теперь выделяем полный квадрат при переменной х₂, коэффициент при которой отличен от нуля:

.

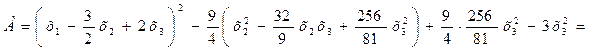
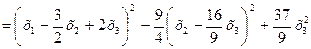Итак, невырожденное линейное преобразование

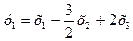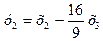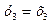, , приводит квадратичную форму к каноническому виду:

.

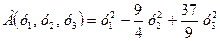3)Для установления знакоопределенности квадратичной формы применяют критерий Сильвестра:

Для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы были положительны, т.е.

, , ,…, .

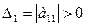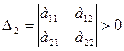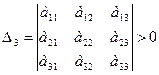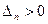Для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка, т.е. , , 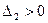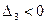. Т.о. .миноры нечетного порядка отрицательны, четного порядка – положительны.

Для неопределенных квадратичных форм знаки главных миноров принимают как положительные, так и отрицательные значения.

Матрица А квадратичной формы имеет вид:

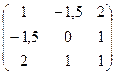
Главные миноры матрицы А:

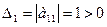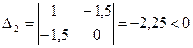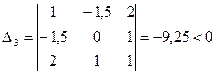, , , следовательно, данная квадратичная форма неопределенная.

Для того, чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 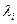матрицы А были положительны (отрицательны). Рассмотрим на примере.

Разберите решение задачи 9.

Доказать, что квадратичная форма 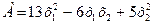положительно определенная

Решение:

Первый способ. Матрица А квадратичной формы имеет вид: 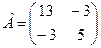. Характеристическое уравнение матрицы А:

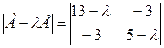или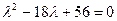

Решая уравнение, получим 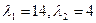. Т.к. корни характеристического уравнения матрицы А положительны, то данная квадратичная форма положительна.

Второй способ. Так как главные миноры матрицы А

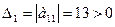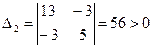, положительны, то по критерию Сильвестра данная квадратичная форма положительно определенная.

Вопросы для самопроверки

1. Дайте определение n-мерного линейного векторного пространства.

2. Понятие линейная зависимости и независимости векторов линейного пространства.

3. Размерность и базис линейного пространства.

4. Переход к новому базису. Как найти матрицу перехода?

5. Дайте определение линейного подпространства. Как найти сумму и пересечение линейных подпространств?

6. Дайте понятие линейных отображений.

7. Дайте понятие линейных операторов

8. Как найти собственные векторы и собственные значения линейного оператора?

9. Дайте понятие квадратичной формы.

10. Назовите алгоритм приведения квадратичной формы к каноническому виду.

11. Как применить критерий Сильвестра знакоопределенности квадратичной формы?