 |
Главная |
Линейная алгебра. Векторная алгебра. Евклидово пространство
|
из
5.00
|
Задание 1.

 Замечание. Здесь и далее верные варианты ответов помечены точкой и подчеркнуты.
Замечание. Здесь и далее верные варианты ответов помечены точкой и подчеркнуты.
Решение.
Пусть дана система линейных алгебраических уравнений:

По правилу Крамера  если Δ ≠ 0.
если Δ ≠ 0.



В данном случае:

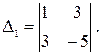
Задание 2.


Решение.
Пусть даны матрица А размерности  и матрица В размерности
и матрица В размерности 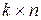 . Произведением матрицы А на матрицу В называется новая матрица С = А · В размерности
. Произведением матрицы А на матрицу В называется новая матрица С = А · В размерности  . В данном случае
. В данном случае  ;
;  ;
;  Элементы матрицы С вычисляются по формуле:
Элементы матрицы С вычисляются по формуле:

В данном случае: 
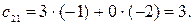
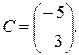
Задание 3 .


Решение.
Разложение определителя по элементам второй строки имеет вид: 


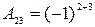

Задание 4.

Пояснения.
Первое утверждение верно. Ранг матрицы по определению равен k, если существует хотя бы один отличный от нуля минор порядка k и все миноры высших порядков равны нулю. Ранг матрицы равен числу линейно независимых строк и столбцов этой матрицы.
Второе утверждение верно. Если все миноры порядка k -1 равны нулю, то и минор порядка k равен нулю.
Третье утверждение не верно, т.к. общее число строк и столбцов матрицы может быть больше числа линейно независимых строк и столбцов этой матрицы 
Четвертое утверждение абсурдно.
Задание 5.


Решение.
Пусть даны два n-мерных вектора 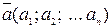 и
и  .
.
Скалярным произведением этих векторов называется число:
 .
.
Угол между векторами  и
и  определяется формулой:
определяется формулой: 
Если угол φ тупой, то  или
или 
В данном случае: 

Задание 6.


Решение.
Векторы 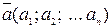 и
и  называются ортогональными, если их скалярное произведение равно нулю:
называются ортогональными, если их скалярное произведение равно нулю: 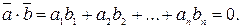
В данном случае  .
.

Задание 7.


Решение.
Вектор называется нормированным, если его модуль равен единице. В данном случае:  ;
;
 ;
;
 ;
;  ;
;  ;
; 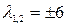 .
.
Аналитическая геометрия на плоскости и в пространстве
Задание 1.

Решение.
Воспользуемся уравнением прямой, проходящей через точку K в заданном направлении (перпендикулярно прямой MN):
 .
.
По условию перпендикулярности  .
. 

Искомое уравнение принимает вид: 
Задание 2 .

Решение.
Уравнение окружности с центром в точке  определяется уравнением:
определяется уравнением:


Координаты центра заданы, поэтому достаточно определить радиус. Для этого используем условие прохождения искомой окружности через точку А(10;10); т.е. подставим координаты точки А в уравнение окружности.

Тогда, уравнение окружности принимает вид:

Задание 3.

Пояснения.
Общее уравнение плоскости имеет вид:

Если в уравнении отсутствует некоторая переменная, например z, то плоскость параллельна соответствующей оси, например Oz. Если отсутствует свободный член, то плоскость проходит через начало координат.
Задание 4.


Решение.
Угловой коэффициент определяется формулой:

Разделы «Комплексные числа», «Действия над комплексными числами», «Тригонометрическая форма комплексного числа» являются составными частями дидактической единицы «Комплексный анализ»
Задание 5.


Решение.
Тригонометрическая форма комплексного числа  имеет вид:
имеет вид:  , где
, где  ;
;  .
.
В данном случае по геометрической иллюстрации видно, что  и
и 
 . Значит
. Значит 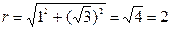 и
и 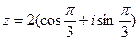 .
.
|
из
5.00
|
Обсуждение в статье: Линейная алгебра. Векторная алгебра. Евклидово пространство |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

