Задания для самостоятельного решения. В задачах 1-20 выяснить, образуют ли базис векторы Если образуют

В задачах 1-20 выяснить, образуют ли базис векторы 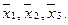Если образуют, то разложить вектор 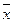по этому базису:

1.

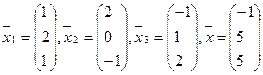
2.

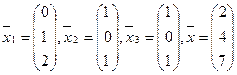
3.

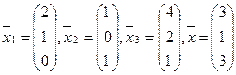
4.

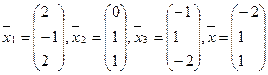
5.

6.

7.

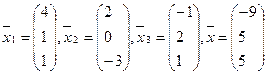
8.

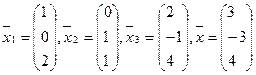
9.

10.

11.

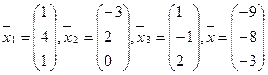
12.

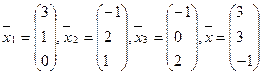
13.

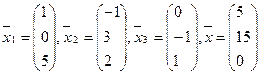
14.

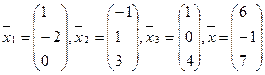
15.

16.

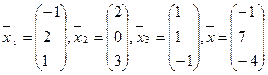
17.

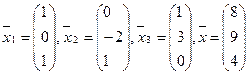
18.

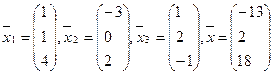
19.

20.

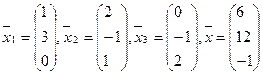
В задачах 21-40 задана матрица А линейного оператора в некотором базисе . Найти матрицу этого оператора в базисе .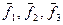

21. А=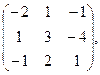

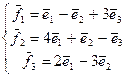
22.А=

23. А=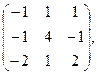

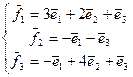
24. А=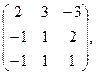

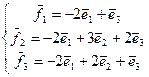
25. А=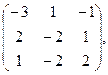

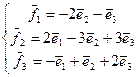
26. А=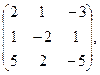

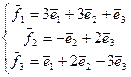
27. А=

28. А=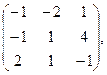

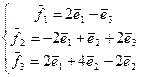
29. А=

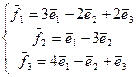
30. А=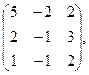

 

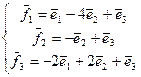
31. А=

 

32. А=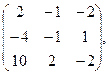

33. А=

 

34. А=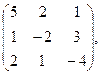

 

35. А=

 

36. А=

 

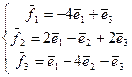
37. А=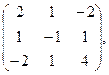

 

38. А=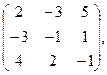

 

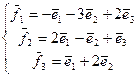
39. А=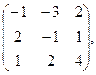

 

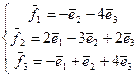
40. А=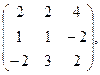

В задачах 41-60 найти собственные значения и собственные векторы линейного оператора, заданного матрицей А. Привести матрицу А к диагональному виду:

 

41. А=42. А=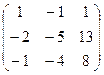43. А=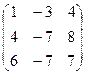

 

44. А=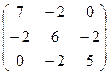45. А=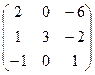46. А=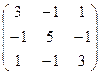

 

47. А=48. А=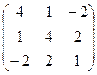49. А=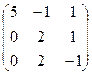

50. А=51. А=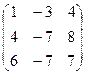52. А=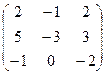

53. А=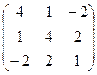54. А=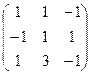55. А=

 

56. А=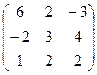57. А=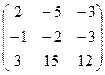58. А=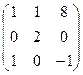

 

59. А=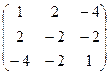60. А=

В задачах 61-80 задана квадратичная форма :

1) найти матрицу А квадратичной формы в каноническом базисе (в матричном виде);

2) привести квадратичную форму к каноническому виду методом Лагранжа (к сумме квадратов соответствующих координат выделением полных квадратов);

Доказать, что квадратичная форма А положительно или отрицательно определенная.

61.

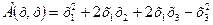
62.

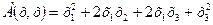
63.

64.

65.

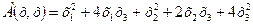
66.

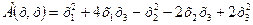
67.

68.

69.

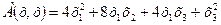
70.

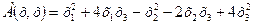
71.

72.

73.

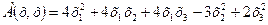
74.

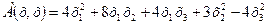
75.

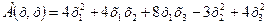
76.

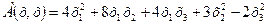
77.

78.

79.

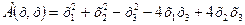
80.

Аналитическая геометрия на плоскости.

Литература: [1] гл.4; [2] гл.7-8; [3] гл.3; [4] гл.3; [5] гл.1; [6] гл.4.

Разберите решение задачи 10.

Даны координаты вершин треугольника АВС: А(1,5); В(-4,0); С(4,-4).

1) составить уравнения медианы АD, высоты АЕ;

2) найти длину высоты АЕ и медианы АD;

3) определить угол между высотой АЕ и медианой АD;

4) составить уравнение средней линии DМ параллельной стороне АС;

5) составить уравнение окружности, проходящей через точки А, В, С;

Составить систему линейных неравенств, определяющих треугольник АВС.

Решение.

1.

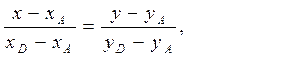Уравнение медианы АD определяем по формуле

Где точка D делит отрезок ВС пополам.

Координаты точки D:

 

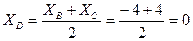
,D(0; -2)

Тогда, 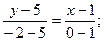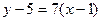или (АD)

Для составления уравнения высоты АЕ воспользуемся условием перпендикулярности двух прямых ВС и АЕ: .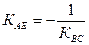

Угловой коэффициент прямой ВС найдем по координатам точек В и С:

тогда .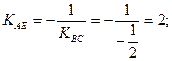

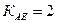Составим уравнение высоты АЕ, используя уравнение прямой, проходящей через точку А в заданном направлении:

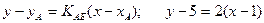или (АЕ)

2. Длину высоты АЕ определяем, используя формулу для определения расстояния точки А (1;5) от прямой ВС:

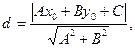
где (х_о; у_о) – координаты точки А (1;5);

А,В,С – коэффициенты уравнения прямой ВС.

Угловой коэффициент прямой ВС К_вс = .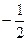

Воспользуемся уравнением прямой, проходящей через точку в заданном направлении:

у-у_в = К_вс (х-х_в)

у-0 = 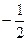(х+4); 2у=-х-4 или х+2у+4=0.

Отсюда А=1; В=2; С=4.

.

Длину медианы АD определим, используя формулу для определения расстояния между двумя точками А и D:

.

3. Угол между высотой АЕ и медианой АD находим, используя формулу

,

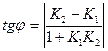где К₁ – угловой коэффициент прямой АЕ, К₁=2;

К₂ – угловой коэффициент прямой АD находим из уравнения 7х-у-2=0, разрешив его относительно у: у=7х-2, отсюда К₂=7.

 

.

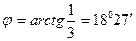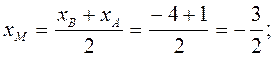
4. Средняя линия DМ треугольника АВС проходит через середины сторон ВС и АВ, т.е. проходит через точки D и 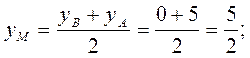М:

М .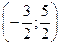

Уравнение средней линии запишем используя уравнение прямой, проходящей через две точки:

; ;

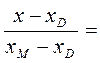
9х+3у+6=0 или 3х+у+2=0 (DМ).

5. Уравнение окружности радиусаR c центром в точке Q (х_о;у_о) имеет вид: (х-х_о)²+(у-у_о)² = R² . так как точки А,В и С лежат на окружности, то их координаты должны удовлетворять этому уравнению:

Из первого уравнения вычтем второе уравнение, затем из первого уравнения вычтем третье уравнение. Из полученных уравнений составим систему уравнений:

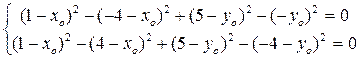
или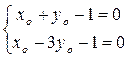

Решаем полученную систему уравнений по формулам Крамера:

;

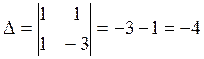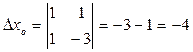
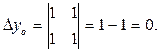
Тогда 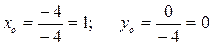. Q (1;0).

Найдем радиус окружности, подставив найденные значения х_о=1 и у_о=0 в любое из трех уравнений:

(1-1)²+(5-0)²=R²,

Отсюда R² =25, R=5.

Уравнение окружности (х-1)²+у² =25.

 

6. Для составления системы линейных неравенств, определяющих треугольник АВС,составим уравнения сторон треугольника АВС.

 

Уравнение стороны АВ определим по формуле: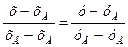

 

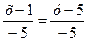, или , .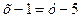

 

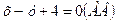Уравнение стороны ВС определим по формуле: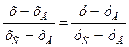

 

, , , , .

 

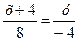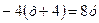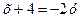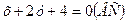Уравнение стороны АС определим по формуле:

 

, , , , .

 

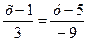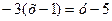Областью решений неравенства является полуплоскость. Областью решений системы неравенств является треугольник, ограниченный полуплоскостями. Для составления неравенства выбираем произвольную точку, лежащую в какой-либо из полуплоскостей. Лучше выбрать точку начала координат (0;0). Подставляем (0;0) в первое уравнение 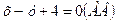, получим 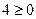, т.е. получаем неравенство 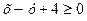. Аналогично получим 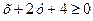и

.

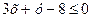Таким образом, система линейных неравенств, определяющих треугольник АВС:

 

 

На рис.1 в декартовой прямоугольной системе координат хОу изображены треугольник АВС, медиана АD, высота АЕ, биссектриса АF и окружность, проходящая через точки А, В, С и система линейных неравенств, определяющих треугольник АВС.

 

 

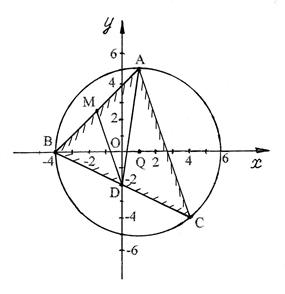
Рис. 1. Графическое пояснение к задаче 10