 |
Главная |
П. 5. Определение группы
|
из
5.00
|
Опр.6. Пусть  , * - бинарная операция на множестве
, * - бинарная операция на множестве  .
.  называется группой, если выполняются следующие условия (аксиомы группы):
называется группой, если выполняются следующие условия (аксиомы группы):
1)  , т.е. операция * ассоциативна;
, т.е. операция * ассоциативна;
2)  , т.е. в множестве
, т.е. в множестве  существует нейтральный относительно операции * элемент;
существует нейтральный относительно операции * элемент;
3)  , т.е. для каждого элемента а множества
, т.е. для каждого элемента а множества  существует в множестве
существует в множестве  симметричный к нему элемент
симметричный к нему элемент 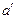 .
.
Опр.7. Группа  называется коммутативной (абелевой), если операция * коммутативна.
называется коммутативной (абелевой), если операция * коммутативна.
Опр.8. Группа  называется конечной, если
называется конечной, если  - конечное множество; при этом число элементов множества
- конечное множество; при этом число элементов множества  называют порядком группы
называют порядком группы  .
.
Если  - бесконечное множество, то группа
- бесконечное множество, то группа  называется бесконечной группой.
называется бесконечной группой.
Свойства группы
1) Нейтральный элемент в группе единственный (теорема 1).
2) Каждый элемент группы имеет единственный симметричный к нему элемент (теорема 2).
3)  . Симметричный к симметричному для элемента а элемент есть сам элемент а.
. Симметричный к симметричному для элемента а элемент есть сам элемент а.
Доказательство: По определению симметричного элемента имеем, что  . Тогда
. Тогда  . ▲
. ▲
4) В группе выполняются законы сокращения, т.е.  и
и 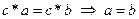 .
.
Доказательство: Пусть  . Тогда
. Тогда
 .
.
Аналогично доказывается другой закон сокращения. ▲
5) В группе  каждое из уравнений
каждое из уравнений  и
и  имеет единственное решение для любых
имеет единственное решение для любых  .
.
Доказательство: Действительно, т.к.  , то элемент
, то элемент  является решением уравнения
является решением уравнения  .
.
Если с -ещё одно решение этого уравнения, т.е.  , то имеем
, то имеем
 , т.е.
, т.е.  . ▲
. ▲
6) 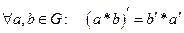 (Теорема 2).
(Теорема 2).
Аддитивная и мультипликативная запись группы
Аддитивная запись
Пусть  , «+» - бинарная операция на
, «+» - бинарная операция на  .
.  -группа, если:
-группа, если:
1)  ;
;
2)  ;
;
3)  .
.
Группу  при этом называют группой по сложению или аддитивной группой.
при этом называют группой по сложению или аддитивной группой.
Мультипликативная запись
Пусть  , «∙» - бинарная операция на
, «∙» - бинарная операция на  .
.  -группа, если:
-группа, если:
1)  ;
;
2)  ;
;
3)  .
.
Группу  при этом называют группой по умножению или мультипликативной группой.
при этом называют группой по умножению или мультипликативной группой.
Примеры групп:
1. Аддитивные группы целых, рациональных, действительных, комплексных чисел. При этом они абелевы (всякое кольцо есть группа по сложению).
2. Множество целых четных чисел аддитивная абелева группа.
3. Множество отличных от нуля элементов любого поля образует абелеву группу по умножению. Эта группа называется мультипликативной группой поля.
Таким образом, мы имеем мультипликативные группы полей рациональных, действительных и комплексных чисел.
4. Группу по умножению составляют все положительные действительные числа. Эта группа коммутативна.
5. Пусть  - множество всех корней n-степени из 1 в поле
- множество всех корней n-степени из 1 в поле  комплексных чисел. Известно, что
комплексных чисел. Известно, что  - конечное множество, содержащее n элементов, т.е. все корни находятся по формуле
- конечное множество, содержащее n элементов, т.е. все корни находятся по формуле  Легко проверить, что
Легко проверить, что  - группа по умножению, притом абелева и конечная порядка n.
- группа по умножению, притом абелева и конечная порядка n.
Этот пример показывает, что для любого натурального числа n существует конечная мультипликативная группа порядка n.
6. Пусть m - натуральное число.  - множество классов вычетов по модулю m. Это множество по сложению образует абелеву конечную группу порядка m. Нейтральным элементом группы
- множество классов вычетов по модулю m. Это множество по сложению образует абелеву конечную группу порядка m. Нейтральным элементом группы  является класс
является класс  , противоположным элементом для класса
, противоположным элементом для класса  является класс
является класс  .
.
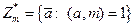 - мультипликативная группа.
- мультипликативная группа.
7. Множество всех движений плоскости (пространства) относительно их композиции образует группу, притом коммутативную. Действительно, из геометрии известно, что композиция  движений f и g есть снова движение; преобразование
движений f и g есть снова движение; преобразование  , обратное движению f, есть также движение; тождественное преобразование, очевидно, является движением, ассоциативный закон
, обратное движению f, есть также движение; тождественное преобразование, очевидно, является движением, ассоциативный закон  выполняется для любых преобразований.
выполняется для любых преобразований.
8. Аналогично устанавливается, что множество всех подобий плоскости (пространства), множество всех аффинных преобразований плоскости (пространства) являются группами относительно композиции преобразований.
9. Множество всех квадратных матриц n-ого порядка над полем P является аддитивной абелевой группой.
10. Множество всех обратимых квадратных матриц n-oго порядка на полем P - мультипликативная группа; при  некоммутативна.
некоммутативна.
11. Пусть  - конечное n-элементное множество. Взаимно однозначное отображение
- конечное n-элементное множество. Взаимно однозначное отображение  называется подстановкой n-ной степени.
называется подстановкой n-ной степени.
Подстановку 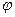 обычно записывают в следующем виде:
обычно записывают в следующем виде:  , указывая во второй строке образы чисел 1, 2,…, п, т.е.
, указывая во второй строке образы чисел 1, 2,…, п, т.е.  . Известно, что существует п! подстановок п-ной степени. Умножение
. Известно, что существует п! подстановок п-ной степени. Умножение  двух подстановок - это результат выполнения сначала подстановки
двух подстановок - это результат выполнения сначала подстановки 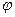 , а затем подстановки
, а затем подстановки  . Множество
. Множество  всех подстановок п-ной степени есть группа по умножению, при этом конечная, порядка п!. Эта группа при
всех подстановок п-ной степени есть группа по умножению, при этом конечная, порядка п!. Эта группа при  является некоммутативной. Она называется симметрической группой п-ной степени.
является некоммутативной. Она называется симметрической группой п-ной степени.
12. Множество  всех четных подстановок п-ной степени также образует группу по умножению. Эта группа конечна и имеет порядок
всех четных подстановок п-ной степени также образует группу по умножению. Эта группа конечна и имеет порядок  при
при  . При
. При 
 - некоммутативная группа, а группа
- некоммутативная группа, а группа 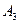 коммутативна. Группа
коммутативна. Группа  называется знакопеременной группой п-ной степени.
называется знакопеременной группой п-ной степени.
ВОПРОС № 2 Определение кольца. Свойства. Коммутативные кольца. Делители нуля. Примеры колец.
Опр.1. Непустое множество К, в котором определены две бинарные операции – сложение «+» и умножение «×», называется кольцом, если выполняются следующие условия (аксиомы кольца):
1)  для всех а и b из К;
для всех а и b из К;
2)  для всех
для всех  ;
;
3) существует элемент  такой, что
такой, что  для любого
для любого  (элемент 0 – нулевой элемент кольца);
(элемент 0 – нулевой элемент кольца);
4) для каждого элемента  существует элемент
существует элемент 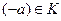 такой, что
такой, что 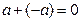 (элемент (- а) при этом называют противоположным для элемента а);
(элемент (- а) при этом называют противоположным для элемента а);
5)  для всех
для всех  ;
;
6)  для всех
для всех  .
.
Часто в математике рассматривают кольца, удовлетворяющие дополнительным требованиям.
Опр.2. Кольцо К называется коммутативным, если умножение удовлетворяет условию коммутативности, т.е.  для всех
для всех  .
.
Опр.3. Если в кольце К имеется такой элемент 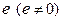 , что
, что  для всех
для всех  , то говорят, что К -кольцо с единицей, а элемент
, то говорят, что К -кольцо с единицей, а элемент  называют единицей кольца.
называют единицей кольца.
Аксиомы 1) – 4) показывают, что любое кольцо является абелевой (коммутативной) группой по сложению, которую называют аддитивной группой кольца.
Из свойств групп следует, что во всяком кольце выполняются следующие свойства:
I.В кольце К существует единственный нулевой элемент.
II.Каждый элемент а кольца К имеет единственный противоположный элемент  .
.
III.В кольце имеет место закон сокращения, т.е.  ,
,  .
.
IV.  .
.
V.  .
.
VI.Уравнение 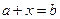 для любых элементов
для любых элементов  имеет единственное решение
имеет единственное решение  .
.
Сумма  обозначается
обозначается  и называется разностью элементов
и называется разностью элементов  и а. Таким образом, в кольце появляется еще одна бинарная операция – вычитание, при этом
и а. Таким образом, в кольце появляется еще одна бинарная операция – вычитание, при этом  .
.
Отметим некоторые свойства разности:
1) 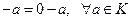 . Действительно,
. Действительно,  .
.
2)  . Действительно,
. Действительно,  .
.
3)  . Действительно,
. Действительно, 
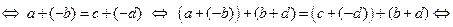
 .
.
4) 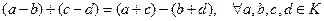 . Действительно,
. Действительно, 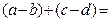
 .
.
5)  . Действительно,
. Действительно, 


Дальнейшие свойства кольца:
VII. 
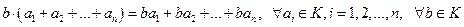 .
.
VIII. 
Свойства VII и VIII легко доказываются методом математической индукции.
IX.  , т.е. дистрибутивные законы выполняются и для разности элементов кольца.
, т.е. дистрибутивные законы выполняются и для разности элементов кольца.
Действительно, 
 .
.
X. 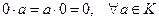 .
.
Действительно, 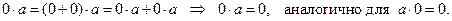
XI.  .
.
Действительно, 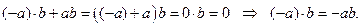
Аналогично 
 («минус» на «минус» дает «плюс»)
(«минус» на «минус» дает «плюс»)
XII.  .
.
Действительно, 
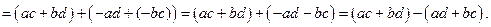
Опр.4. Элементы  называются делителями нуля, если
называются делителями нуля, если  , но
, но 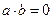 .
.
Примеры колец:
1. Каждое из следующих множеств –  является кольцом. Все они являются коммутативными кольцами с единицей и не содержат делителей нуля.
является кольцом. Все они являются коммутативными кольцами с единицей и не содержат делителей нуля.
2. Множество всех четных целых чисел является коммутативным кольцом без единицы и делителей нуля.
3. Множество  является коммутативным кольцом с единицей и без делителей нуля.
является коммутативным кольцом с единицей и без делителей нуля.
4. Множество  классов вычетов по модулю m является коммутативным кольцом с единицей
классов вычетов по модулю m является коммутативным кольцом с единицей  . При составном модуле m кольцо
. При составном модуле m кольцо  содержит делители нуля. Например, в кольце
содержит делители нуля. Например, в кольце  классы вычетов
классы вычетов  являются делителями нуля, т.к.
являются делителями нуля, т.к.  , но
, но  .
.
5. Множество  квадратных матриц n-ого порядка над полем действительных чисел
квадратных матриц n-ого порядка над полем действительных чисел  является кольцом с единицей. Единицей является матрица
является кольцом с единицей. Единицей является матрица  . Это кольцо некоммутативное при
. Это кольцо некоммутативное при  и содержит делители нуля. Например, в кольце
и содержит делители нуля. Например, в кольце  если
если 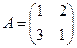 ,
, 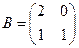 , то
, то 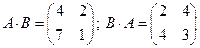 и мы видим, что
и мы видим, что  . Матрицы
. Матрицы 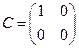 и
и  отличны от нуля – нулевой матрицы
отличны от нуля – нулевой матрицы  , но
, но  .
.
6. Множество функций, определенных для всех действительных значений х и принимающих действительные значения, является коммутативным кольцом с единицей. Сложение и умножение функций определяется при этом «поточечно»: 
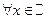 ,
, 
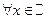 . Нулевой элемент - функция
. Нулевой элемент - функция  , единичный элемент - функция
, единичный элемент - функция  . В этом кольце имеются делители нуля, например, следующие функции:
. В этом кольце имеются делители нуля, например, следующие функции: 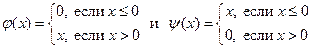 .
.
7. Множество многочленов от переменной х с коэффициентами из поля Р образует кольцо  . Это кольцо коммутативное, содержит единицу и не имеет делителей нуля.
. Это кольцо коммутативное, содержит единицу и не имеет делителей нуля.
ВОПРОС № 3 Определение поля. Свойства. Характеристика поля. Примеры полей.
Опр.1. Полем называется множество Р, в котором определены 2 бинарные операции – сложение «+» и умножение «×», удовлетворяющие следующим условиям (аксиомы поля):
10 Сложение ассоциативно, т.е. 
20 Сложение коммутативно, т.е. 
30  (0 - нулевой элемент);
(0 - нулевой элемент);
40  (-а - противоположный к элементу а элемент);
(-а - противоположный к элементу а элемент);
50 Умножение ассоциативно, т.е. 
60 Умножение коммутативно, т.е. 
70  (е - нейтральный элемент);
(е - нейтральный элемент);
80  (
(  - обратный к элементу а элемент);
- обратный к элементу а элемент);
90 Имеет место дистрибутивный закон умножения относительно сложения (т.е. умножение и сложение связаны дистрибутивным законом):  .
.
Видим, что поле является кольцом (10, 20, 30, 40, 50, 90), причем коммутативным (60) и с единицей (70).
Поэтому можно дать другое определение поля:
Полем называется коммутативное кольцо с единицей, в котором  и любой ненулевой элемент обратим (т.е. имеет обратный элемент).
и любой ненулевой элемент обратим (т.е. имеет обратный элемент).
Поэтому в поле справедливы все свойства кольца, а именно:
1) В поле P существует единственный нулевой элемент.
2) Каждый элемент поля P имеет единственный противоположный элемент.
3) В поле P имеет место закон сокращения:  .
.
4) Уравнение 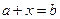 имеет единственное решение
имеет единственное решение  , которое называется разностью элементов b и a обозначается
, которое называется разностью элементов b и a обозначается  , т.е. в поле P можно рассматривать бинарную операцию – вычитание и установить все свойства вычитания.
, т.е. в поле P можно рассматривать бинарную операцию – вычитание и установить все свойства вычитания.
5) Единичный элемент поля P единственный.
6) 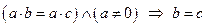 .
.
Доказательство: Пусть  , тогда, т.к.
, тогда, т.к. 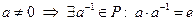 . Значит,
. Значит, 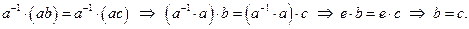 ▲.
▲.
7) Каждый отличный от нуля элемент а имеет единственный обратный к нему элемент.
8)  .
.
9) В поле нет делителей нуля, т.е. нет ненулевых элементов, произведение которых было бы равно нулю.
Доказательство: Покажем, что если 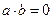 , то
, то  или
или  . Действительно, пусть
. Действительно, пусть 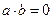 . Если
. Если  , то все доказано. Пусть
, то все доказано. Пусть  , тогда
, тогда  ▲.
▲.
10) Для любых элементов а и b,  поля Р, уравнение
поля Р, уравнение 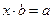 имеет единственное решение
имеет единственное решение  . Это решение данного уравнения называется частным элементов а и b и обозначается
. Это решение данного уравнения называется частным элементов а и b и обозначается  .
.
Итак, частное любых двух элементов а и b,  поля Р однозначно определено и
поля Р однозначно определено и  .
.
Свойства частного:
1.  . Действительно,
. Действительно, 
2. 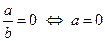 . Действительно
. Действительно 
3.  .
.
Доказательство: 
4. 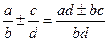 .
.
Доказательство: 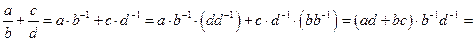
 Разность аналогично.
Разность аналогично.
5.  .
.
Доказательство: 
6. 
Доказательство:  Но из свойства 3) следует, что
Но из свойства 3) следует, что 
 значит
значит 
7. 
Действительно, 
Примеры полей:
1. Каждое из следующих множеств -  является полем.
является полем.
2.  - поле.
- поле.
3. Множество всех дробно-рациональных функций с действительными коэффициентами есть поле, т.е. множество  - поле.
- поле.
4.  - поле;
- поле;  - поле.
- поле.
Все перечисленные поля являются бесконечными, т.е. содержат бесконечно много элементов. Существуют, однако, поля, состоящие из конечного числа элементов.
5. Рассмотрим кольцо  классов вычетов по простому модулю р, то есть
классов вычетов по простому модулю р, то есть  и покажем, что это поле.
и покажем, что это поле.
Доказательство: если 
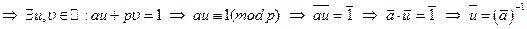 .
.
6. Отметим, что если модуль m не является простым числом, то кольцо  классов вычетов по данному модулю полем не является. Действительно, т.к. m -составное число, то
классов вычетов по данному модулю полем не является. Действительно, т.к. m -составное число, то  такие, что
такие, что  , причем
, причем  и
и  – делители нуля, т.к.
– делители нуля, т.к. 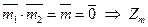 не является полем.
не является полем.
Характеристика поля
Не все свойства числовых полей сохраняются в случае произвольных полей. Так, складывая число 1 само с собою несколько раз, т.е. беря любое целое положительное кратное единицы, мы никогда не получим нуля 0. Это имеет место не для всех полей. Например, рассмотрим поле  , в нем
, в нем 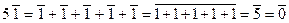 , то есть в поле
, то есть в поле  нашлось целое кратное единицы
нашлось целое кратное единицы  , равное нулю
, равное нулю  .
.
Опр.2. Пусть е – единица поля Р. Наименьшее натуральное число m такое, что  (если оно существует), называется характеристикой поля Р.
(если оно существует), называется характеристикой поля Р.
Если же любое натуральное кратное единицы е поля Р отлично от нуля, то говорят, что поле Р имеет характеристику нуль.
Очевидно, что характеристика поля  , где р -простое число, равна р.
, где р -простое число, равна р.
Справедлива следующая теорема.
Теорема. Характеристикой поля является либо нуль, либо простое число.
Доказательство: Если характеристика поля Р есть нуль, то все доказано.
Пусть она не есть нуль, а натуральное число m и допустим, что m не является простым числом. Число 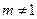 , т.к. в противном случае
, т.к. в противном случае  , чего в поле нет. Так как m -составное число
, чего в поле нет. Так как m -составное число  такие, что
такие, что  , причем
, причем  и
и  . Тогда
. Тогда  (т.к. в поле нет делителей нуля), а это означает, что m не является наименьшим натуральным числом с таким свойством, что противоречит тому, что m -характеристика поля P, значит m -простое число. ▲
(т.к. в поле нет делителей нуля), а это означает, что m не является наименьшим натуральным числом с таким свойством, что противоречит тому, что m -характеристика поля P, значит m -простое число. ▲
ВОПРОС № 4 Определение векторного пространства. Свойства. Примеры векторных пространств.
Опр.1. Пусть  - аддитивная абелева группа, т.е. на
- аддитивная абелева группа, т.е. на  определена бинарная операция «+» такая, что: 1) «+» - ассоциативна;
определена бинарная операция «+» такая, что: 1) «+» - ассоциативна;
2) «+» - коммутативна;
3)  ;
;
4) 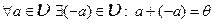 .
.
Р - поле. Пусть также определено действие умножения элементов  на элементы поля Р, т.е. указан закон, по которому
на элементы поля Р, т.е. указан закон, по которому  ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  , который называется произведением λ на а и обозначается
, который называется произведением λ на а и обозначается  . Тогда
. Тогда  называется векторным пространством над полем Р, если:
называется векторным пространством над полем Р, если:
1.  .
.
2.  .
.
3.  .
.
4.  .
.
Элементы  называются векторами, а элементы поля Р – скалярами.
называются векторами, а элементы поля Р – скалярами.
Замечание:  - группа по сложению, нейтральный элемент относительно «+» обозначаем
- группа по сложению, нейтральный элемент относительно «+» обозначаем  . Нулевой элемент поля Р обозначаем 0.
. Нулевой элемент поля Р обозначаем 0.
Свойства:
Так как  - группа относительно «+», то для
- группа относительно «+», то для  выполнены все свойства группы, а именно: 1) нулевой вектор
выполнены все свойства группы, а именно: 1) нулевой вектор  единственный;
единственный;
2) Для любого вектора  существует единственный противоположный вектор
существует единственный противоположный вектор 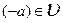 ;
;
3) Уравнение 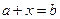 имеет единственное решение
имеет единственное решение 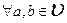 . Это решение
. Это решение  обозначается
обозначается  и называется разностью векторов
и называется разностью векторов  .
.
Отметим дальнейшие простейшие свойства векторного пространства:
4)  (0 – нулевой элемент поля Р,
(0 – нулевой элемент поля Р,  - нулевой вектор из
- нулевой вектор из  ).
).
Доказательство: 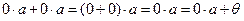 . Итак,
. Итак, 
5)  .
.
Доказательство:  .
.
6) Если  , то
, то 
Доказательство: пусть  и
и  , покажем, что тогда
, покажем, что тогда  Так как
Так как  , то
, то  Теперь имеем, что
Теперь имеем, что 
7)  .
.
Доказательство: 
8)  .
.
Доказательство: 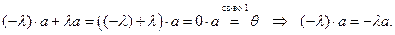
9)  .
.
Доказательство: 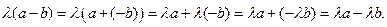
|
из
5.00
|
Обсуждение в статье: П. 5. Определение группы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

