 |
Главная |
П. 3. Делимость многочленов
|
из
5.00
|
Пусть  - кольцо многочленов одной переменной х над полем Р.
- кольцо многочленов одной переменной х над полем Р.
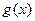
 Опр.3. Пусть
Опр.3. Пусть 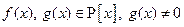 . Говорят, что делится на (и пишут
. Говорят, что делится на (и пишут  ), если
), если  .
.
Свойства делимости многочленов:
1)  .
.
2)  .
.
Так как 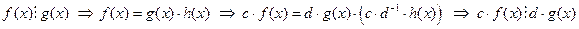 .
.
3)  .
.
Теорема 2 (о делении многочленов с остатком). Для любых многочленов 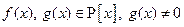 существуют единственные многочлены
существуют единственные многочлены  такие, что
такие, что  , при этом
, при этом 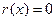 или
или  .
.
(Знать определение степени многочлена, высшего (старшего) члена многочлена).
Доказательство: 1. Возможность деления с остатком. Пусть 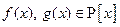 ,
,  .
.
1 случай. Если  или
или  , то
, то  и существование представления доказано.
и существование представления доказано.
2 случай. Пусть теперь 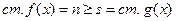 ,
,  ,
,  .
.
Рассмотрим многочлен  .
.  , так как
, так как
многочлены  и
и  имеют одинаковые высшие члены
имеют одинаковые высшие члены  , которые при вычитании взаимно уничтожаются.
, которые при вычитании взаимно уничтожаются.
Если  или
или 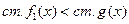 , то процесс закончен и искомое представление
, то процесс закончен и искомое представление  .
.
Пусть теперь  и старший коэффициент многочлена
и старший коэффициент многочлена  равен
равен  , то строим многочлен
, то строим многочлен  . Аналогично устанавливаем, что
. Аналогично устанавливаем, что  .
.
Если  или
или  , то процесс закончен.
, то процесс закончен.
Пусть теперь 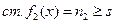 , старший коэффициент
, старший коэффициент  равен
равен  . Строим многочлен
. Строим многочлен  .
.  .
.
И так далее…
Получим многочлены  , степени которых, являясь целыми неотрицательными числами, удовлетворяют неравенствам:
, степени которых, являясь целыми неотрицательными числами, удовлетворяют неравенствам:  Следовательно, через конечное число шагов получим такой многочлен
Следовательно, через конечное число шагов получим такой многочлен  , что
, что  или
или  .
.  .
.
Сложив почленно равенства  ,
,  ,
,  ,…,
,…,  , получим
, получим








 . То есть
. То есть  , возможность деления с остатком доказана.
, возможность деления с остатком доказана.
2. Единственность деления с остатком.
Допустим, что 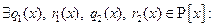
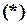
 , где
, где  или
или 
 , где
, где  или
или 
Отсюда имеем: 

Если  , то есть
, то есть  , то так как
, то так как  , то из равенства
, то из равенства  имеем, что
имеем, что  и единственность деления с остатком доказана.
и единственность деления с остатком доказана.



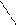 Пусть теперь
Пусть теперь  . Тогда из равенств
. Тогда из равенств 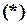
 . Если при этом
. Если при этом  , то
, то 
 . Значит
. Значит  и
и  . Единственность деления с остатком доказана. ▲.
. Единственность деления с остатком доказана. ▲.
Пример: Разделить многочлен  на
на  .
.

Значит  .
.
ВОПРОС № 12 Алгоритм Евклида для целых чисел и для многочленов. НОД и НОК.
Опр.1. Пусть  - целые числа, из которых хотя бы одно отлично от нуля. Наибольшим общим делителем чисел а1,…,аk называется такое целое число
- целые числа, из которых хотя бы одно отлично от нуля. Наибольшим общим делителем чисел а1,…,аk называется такое целое число  , что:
, что:
1)  ;
;
2)  - общий делитель этих чисел (то есть
- общий делитель этих чисел (то есть  ).
).
3)  делится на любой общий делитель чисел
делится на любой общий делитель чисел  .
.
Обозначается НОД чисел  так:
так:  .
.
Теорема 1. Если НОД целых чисел  существует, то он определяется однозначно.
существует, то он определяется однозначно.
Доказательство: Пусть  и
и  .
.
Так как 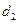 - общий делитель
- общий делитель  , а
, а  - их НОД, то
- их НОД, то 
 .
.
Так как  - общий делитель
- общий делитель  , а
, а 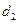 - их НОД, то
- их НОД, то 
 .
.
А так как  ,
,  , то из
, то из  и
и 

 . ▲.
. ▲.
Теорема 2. НОД целых чисел  равен НОД их модулей, то есть
равен НОД их модулей, то есть 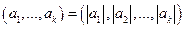 .
.
Поэтому в дальнейшем можно рассматривать НОД натуральных чисел.
Алгоритм Евклида
Опишем способ отыскания НОД двух натуральных чисел, который носит название «алгоритм Евклида».
Пусть 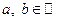 . Делим
. Делим 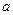 на
на  с остатком:
с остатком:  ,
,  .
.
Если  , то процесс закончен и
, то процесс закончен и  .
.
Если  , то делим
, то делим  на
на 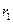 с остатком:
с остатком:  ,
,  .
.
Если  , то процесс закончен, если
, то процесс закончен, если  , делим
, делим 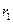 на
на 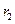 :
:  ,
,  .
.
Поскольку остатки, являясь неотрицательными целыми числами, убывают, то процесс деления оборвётся и на каком-то шаге мы получим остаток, равный нулю.
Пусть  ,
, 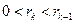
 .
.
Теорема 3. Последний, отличный от нуля, остаток в алгоритме Евклида, составленном для чисел  , является наибольшим общим делителем чисел
, является наибольшим общим делителем чисел  .
.
Доказательство: Пусть 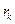 - последний отличный от нуля остаток, тогда:
- последний отличный от нуля остаток, тогда:
1)  .
.
2) Покажем, что 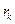 - общий делитель чисел
- общий делитель чисел  . Для этого рассмотрим последовательно равенства алгоритма Евклида, начиная с последнего. Из этого равенства следует, что
. Для этого рассмотрим последовательно равенства алгоритма Евклида, начиная с последнего. Из этого равенства следует, что
 , кроме того,
, кроме того,  . Тогда
. Тогда  , то есть
, то есть  ; затем получим, что
; затем получим, что  и т.д. И, наконец, из второго и первого равенств имеем, что
и т.д. И, наконец, из второго и первого равенств имеем, что  и
и 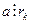 .
.
3) Покажем, что 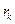 делится на любой общий делитель чисел
делится на любой общий делитель чисел  . Для этого рассмотрим равенства алгоритма, начиная с первого. Пусть
. Для этого рассмотрим равенства алгоритма, начиная с первого. Пусть  - произвольный общий делитель чисел
- произвольный общий делитель чисел  , то есть
, то есть  и
и 
 , то есть
, то есть 
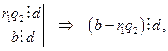
то есть  и т.д. И, наконец,
и т.д. И, наконец,  .
.
Число 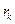 удовлетворяет всем условиям определения НОД чисел
удовлетворяет всем условиям определения НОД чисел 
 . ▲.
. ▲.
Следующая теорема даёт способ отыскания НОД нескольких целых чисел.
Теорема 4. Если  ,
,  , …,
, …,  , то
, то  .
.
НОК целых чисел
Опр.2. Общим кратным целых, отличных от нуля чисел 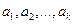 называется целое число с, которое делится на каждое из чисел
называется целое число с, которое делится на каждое из чисел 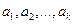 , то есть
, то есть 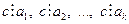 .
.
Опр.3. Целое число т называется наименьшим общим кратным целых, отличных от нуля чисел 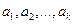 , если: 1)
, если: 1)  ;
;
2) т есть общее кратное чисел 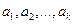 ;
;
3) любое общее кратное чисел 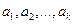 делится на число т.
делится на число т.
Обозначается НОК чисел 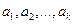 так:
так: 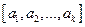 .
.
Теорема 5. Если НОК целых чисел 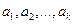 существует, то оно единственно.
существует, то оно единственно.
Теорема 6. НОК целых чисел 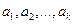 равно НОК их модулей.
равно НОК их модулей.
Доказательства теорем 5 и 6 аналогичны доказательствам теорем 1 и 2.
Теорема 6 позволяет рассматривать НОК только натуральных чисел. Следующая теорема даёт способ отыскания НОК двух натуральных чисел:
Теорема 7.  .
.
Доказательство: покажем, что число  удовлетворяет всем трём условиям определения НОК целых чисел.
удовлетворяет всем трём условиям определения НОК целых чисел.
1) Во-первых,  , так как
, так как  .
.
2) Покажем, что число  есть общее кратное чисел
есть общее кратное чисел  .
.
Обозначим  , причем числа
, причем числа  взаимно просты, то есть
взаимно просты, то есть  .
.
Теперь имеем: 
 .
.
3) Покажем, что любое общее кратное чисел  делится на число
делится на число  .
.
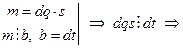 Пусть т – произвольное общее кратное чисел
Пусть т – произвольное общее кратное чисел  , то есть
, то есть 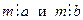 .
.

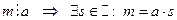 . Но
. Но  , тогда
, тогда
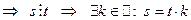 . Теперь имеем:
. Теперь имеем:
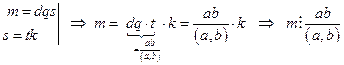 .
.
Следовательно, 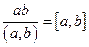 . ▲.
. ▲.
Следующая теорема позволяет находить НОК нескольких чисел:
Теорема 8. Если  ,
,  ,
,  , …,
, …, 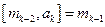 , то
, то  .
.
|
из
5.00
|
Обсуждение в статье: П. 3. Делимость многочленов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

