 |
Главная |
Неприводимые над полем действительных чисел многочлены
|
из
5.00
|
Теорема 4. Пусть  многочлен, степень которого больше единицы, неприводимый над полем действительных чисел
многочлен, степень которого больше единицы, неприводимый над полем действительных чисел  . Тогда существуют такие
. Тогда существуют такие  ,
,  , что многочлен
, что многочлен  ассоциирован с многочленом
ассоциирован с многочленом 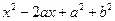 .
.
Доказательство: По основной теореме алгебры многочлен  имеет хотя бы один комплексный корень. Пусть
имеет хотя бы один комплексный корень. Пусть  – корень многочлена
– корень многочлена  , где
, где  . Обязательно
. Обязательно  . Действительно, если допустить, что
. Действительно, если допустить, что  , то
, то 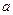 – действительный корень
– действительный корень  , а тогда
, а тогда  делится на многочлен
делится на многочлен  и поскольку степень
и поскольку степень  , то это противоречит неприводимости многочлена
, то это противоречит неприводимости многочлена  над полем
над полем  . Итак,
. Итак,  .
.
Значит  – мнимый корень многочлена
– мнимый корень многочлена  , а тогда, по теореме 3, число
, а тогда, по теореме 3, число  также является корнем многочлена
также является корнем многочлена  . Значит, по следствию из теоремы Безу,
. Значит, по следствию из теоремы Безу,  делится на
делится на  и на
и на  .
.
А тогда  делится на их произведение
делится на их произведение 
 . При этом,
. При этом,  и
и 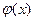 – неприводим над
– неприводим над  (так как не имеет действительных корней). Но
(так как не имеет действительных корней). Но  неприводим над
неприводим над 
 ассоциированы, то есть
ассоциированы, то есть  ▲.
▲.
Следствие: В кольце  неприводимы только многочлены первой степени и многочлены второй степени, ассоциированные с многочленами вида
неприводимы только многочлены первой степени и многочлены второй степени, ассоциированные с многочленами вида 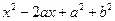 , где
, где  любые действительные числа и
любые действительные числа и  .
.
Теорема 5. Любой многочлен  положительной степени из кольца
положительной степени из кольца  можно единственным образом представить в виде
можно единственным образом представить в виде 
 , где
, где 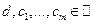 ,
,  .
.  – не имеют действительных корней, то есть
– не имеют действительных корней, то есть  .
.
Следствие 1: Любой многочлен с действительными коэффициентами имеет чётное число мнимых корней.
Следствие 2: Многочлен нечётной степени с действительными коэффициентами имеет хотя бы один действительный корень.
ВОПРОС № 10 Корни многочлена. Отыскание целых и рациональных корней многочлена с целыми коэффициентами.
Пусть  - кольцо многочленов одной переменной х над полем рациональных чисел
- кольцо многочленов одной переменной х над полем рациональных чисел  .
.
Опр.1. Рациональное число с называется корнем многочлена  , если
, если 
Легко видеть, что отыскание рациональных корней многочлена  сводится к отысканию рациональных корней многочлена с целыми коэффициентами. Действительно, если
сводится к отысканию рациональных корней многочлена с целыми коэффициентами. Действительно, если  , то умножив
, то умножив  на общий знаменатель d всех его коэффициентов, мы получим многочлен
на общий знаменатель d всех его коэффициентов, мы получим многочлен  с целыми коэффициентами, имеющий с многочленом
с целыми коэффициентами, имеющий с многочленом  одинаковые рациональные корни, так как
одинаковые рациональные корни, так как  Для отыскания рациональных корней многочлена с целыми коэффициентами существует простой способ, вытекающий из следующей теоремы:
Для отыскания рациональных корней многочлена с целыми коэффициентами существует простой способ, вытекающий из следующей теоремы:
Теорема 1. Если рациональное число  где
где  , является корнем многочлена
, является корнем многочлена  с целыми коэффициентами, то р является делителем свободного члена многочлена
с целыми коэффициентами, то р является делителем свободного члена многочлена  , а q – делителем старшего коэффициента многочлена
, а q – делителем старшего коэффициента многочлена  .
.
Доказательство: Пусть  , где
, где  ,
,  ,
,  .
.
Так как  - корень
- корень  , то
, то  .
. 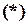
Умножим обе части равенства 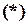 на
на  , получим
, получим

 . Перепишем это равенство в виде:
. Перепишем это равенство в виде:
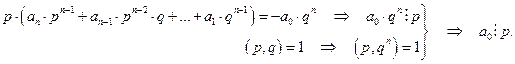
Аналогично, переписав равенство  в виде:
в виде:
 ▲.
▲.
Доказанная теорема дает способ отыскания всех рациональных корней многочлена  с целыми коэффициентами. Этот способ заключается в следующем:
с целыми коэффициентами. Этот способ заключается в следующем:
1) находим все целые делители свободного члена  многочлена
многочлена  :
:  ;
;
2) находим все целые делители старшего коэффициента  многочлена
многочлена  :
:  ;
;
3) составляем все возможные дроби  ,
,  ,
,  .
.
4) Не обязательно все получившиеся числа  будут корнями многочлена
будут корнями многочлена  , но все рациональные корни будут находиться среди этих чисел. Поэтому, вычисляя
, но все рациональные корни будут находиться среди этих чисел. Поэтому, вычисляя  для всех
для всех
этих чисел, мы узнаем, какие из них являются корнями, а какие нет.
Следствие 1: Если целое число т есть целый корень многочлена 
 с целыми коэффициентами, то т является делителем свободного члена
с целыми коэффициентами, то т является делителем свободного члена  .
.
Доказательство:  и по теореме 1
и по теореме 1 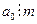 . ▲.
. ▲.
Следствие 2: Рациональный корень нормализованного многочлена 
 с целыми коэффициентами является целым числом.
с целыми коэффициентами является целым числом.
Доказательство: действительно, если  - рациональный корень
- рациональный корень  , то по теореме 1 старший коэффициент многочлена
, то по теореме 1 старший коэффициент многочлена  делится на
делится на  , то есть
, то есть 
 или
или 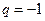

 - целое число. ▲.
- целое число. ▲.
Вычисления, связанные с отысканием рациональных корней многочлена  с целыми коэффициентами могут оказаться громоздкими, потому что делителей у свободного члена и у старшего коэффициента многочлена
с целыми коэффициентами могут оказаться громоздкими, потому что делителей у свободного члена и у старшего коэффициента многочлена  может оказаться много; значит придется подвергать «испытанию на корень» много чисел вида
может оказаться много; значит придется подвергать «испытанию на корень» много чисел вида  .
.
Такие вычисления могут быть значительно сокращены, если воспользоваться следующей теоремой:
Теорема 2. Пусть рациональное число  , где
, где  является корнем многочлена
является корнем многочлена  с целыми коэффициентами. Тогда для любого целого числа т число
с целыми коэффициентами. Тогда для любого целого числа т число 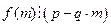 .
.
Доказательство: разделим многочлен  на многочлен
на многочлен  с остатком, тогда по теореме Безу остаток будет равен значению
с остатком, тогда по теореме Безу остаток будет равен значению  многочлена
многочлена  при
при  .
.
Пусть  . Положим
. Положим  , учитывая, что
, учитывая, что  - корень
- корень  , а значит
, а значит  , получим:
, получим:  .
.
Умножим обе части этого равенства на  , получим:
, получим:






 . ▲.
. ▲.
При использовании этой теоремы удобно в качестве т взять целые числа 1 и -1, так как легко вычислить  и
и  . Тогда, если
. Тогда, если  - корень
- корень  , то
, то  и
и  . Покажем на примере, как применять теоремы 1 и 2:
. Покажем на примере, как применять теоремы 1 и 2:
Пример: Найти рациональные корни многочлена  .
.
Делители 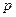 свободного члена 2:
свободного члена 2:  делители
делители  старшего коэффициента 3:
старшего коэффициента 3:  Следовательно, рациональные корни многочлена надо искать среди чисел
Следовательно, рациональные корни многочлена надо искать среди чисел 


 1 и
1 и  не являются корнями
не являются корнями  . Для сокращения числа испытаний составим числа
. Для сокращения числа испытаний составим числа  и
и  . Если
. Если  - корень
- корень  , то оба этих числа должны быть целыми (Ц). Результаты запишем в таблице:
, то оба этих числа должны быть целыми (Ц). Результаты запишем в таблице:

| 
| 
| 
| 
| 
| 
|

| Ц | Ц | Ц | Д | Ц | Д |

| Ц | Ц | Ц | Д |
Испытанию по схеме Горнера подлежат числа 
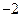
| 
| ||||
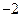
| 
| 
| |||

| 
| 
| 
|
Итак, ни одно из чисел не является корнем многочлена  , значит многочлен не имеет рациональных корней.
, значит многочлен не имеет рациональных корней.
Ответ: многочлен  не имеет рациональных корней.
не имеет рациональных корней.
ВОПРОС № 11 Теорема о делении с остатком для целых чисел и для многочленов.
|
из
5.00
|
Обсуждение в статье: Неприводимые над полем действительных чисел многочлены |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

