Выборочное уравнение прямой линии регрессии

Рассмотрим выборочное уравнение прямой линии среднеквадратичной регрессии Y на X в виде

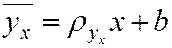, (7.3)

где 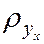– угловой коэффициент прямой линии регрессии, который называют выборочным коэффициентом регрессии Y на X; он является оценкой коэффициента регрессии (раздел 4.4).

Подберём параметры 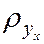и b таким образом, чтобы точки 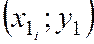, ,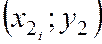…, , построенные на плоскости XоY, лежали как можно ближе к прямой (7.3).

При использовании метода наименьших квадратов (МНК) смысл этого требования интерпретируется так: сумма квадратов отклонений должна быть минимальной. Под отклонением понимают разность 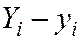, , 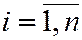где 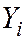– вычисленная по уравнению (7.3) ордината наблюдаемого значения 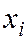; 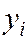– наблюдаемая ордината, соответствующая .

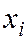Запишем это требование в виде функции:

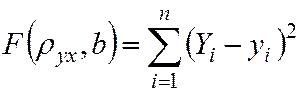
или

.

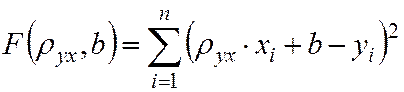Для отыскания минимума функции 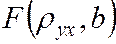приравняем нулю соответствующие частные производные

;

.

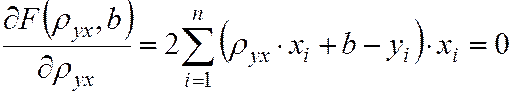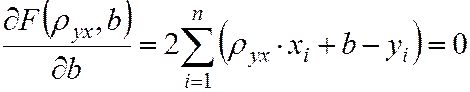Выполнив преобразования, получим систему

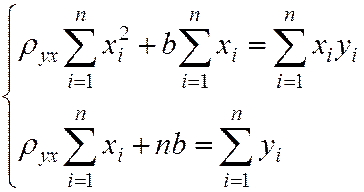
Решив данную систему, найдём искомые параметры

;

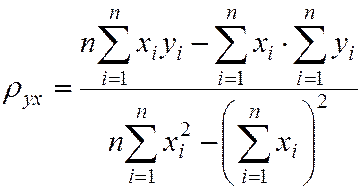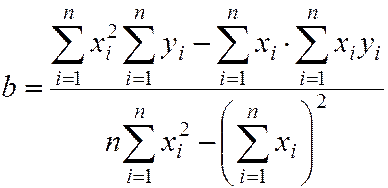. (7.4)

Аналогично можно найти выборочное уравнение прямой линии регрессии X на Y.

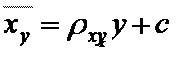. (7.5)

Пример. Найти уравнение прямой линии регрессии по данным наблюдений:

Составляем расчётную таблицу:

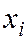
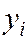
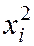
1,00	1,25	1,00	1,250
1,50	1,40	2,25	2,100
3,00	1,50	9,00	4,500
4,50	1,75	20,25	4,875
5,00	2,25	25,00	11,250

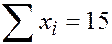
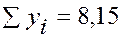
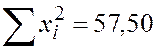
Находим неизвестные параметры из уравнения прямой линии регрессии:

;

.

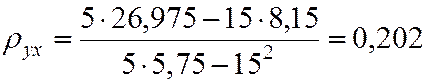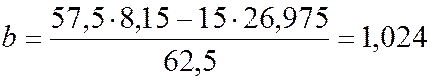Записываем искомое уравнение:

.

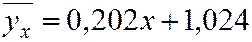Если данные наблюдений представлены в виде корреляционнной таблицы 6.1, то 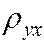можно вычислить по формуле

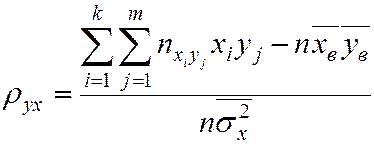. (7.6)

Умножим обе части равенства (7.6) на дробь 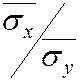, получим формулу (6.3) для вычисления r_в.

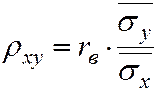. (7.7)

Отсюда уравнение (7.3) можно записать через r_в:

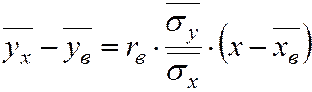. (7.8)

Аналогично уравнение (7.5) примет вид

. (7.9)

Выборочное уравнение нелинейной регрессии

Функции регрессии Y на X могут иметь вид, например, параболической корреляции второго порядка

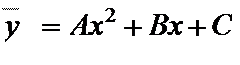, (7.10)

параболической корреляции третьего порядка

,

где A, B, C, D – неизвествные параметры.

Определить неизвестные параметры можно МНК. Для уравнения (7.9) неизвестные параметры A, B, C находят из решения системы линейных уравнений:

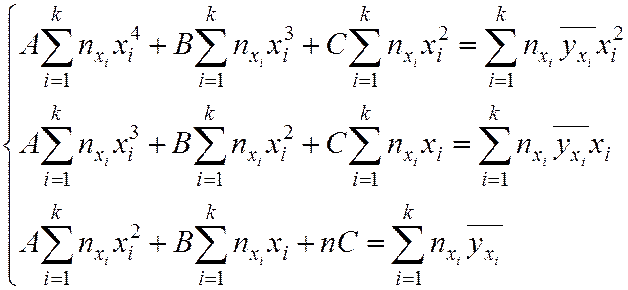
Пример. В. Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике», стр. 276.

Элементы дисперсионного анализа

Общие сведения

Дисперсионный анализ применяют, чтобы установить:

- оказывает ли существенное влияние некоторый качественный фактор 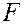, который имеет 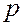уровней 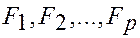на изучаемую величину ;

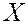- являются ли однородными несколько совокупностей, т.к. однородные совокупности можно объединить в одну и тем самым получить о ней более полную информацию.

Суть дисперсионного анализасостоит в сравнении «факторной дисперсии» (т.е. межгрупповой), обусловленной воздействием фактора, и «остаточной дисперсии» (т.е. внутригрупповой), порождаемой случайными причинами по критерию Фишера-Снедекора.

Различают дисперсионный анализ:

- однофакторный, если исследуется влияние одного фактора на изучаемую СВ;

- многофакторный, если исследуется воздействие нескольких факторов.

Рассмотрим случай однофакторного дисперсионного анализа, когда на изучаемую величину 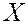влияет только один фактор, который имеет 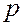постоянных уровней.