 |
Главная |
Скалярное произведение векторов
|
из
5.00
|
Доказательство.
1) Рефлексивность.
Любой базис пространства Vn ориентирован сам с собой одинаково, так как матрица перехода в этом случае единичная и ее определитель равен единице, то есть положителен.
2) Симметричность.
Пусть  и
и  ’ – базисы пространства Vn такие, что
’ – базисы пространства Vn такие, что  ~
~  ’.
’.
Пусть A – матрица перехода от  к
к  ’, B – матрица перехода от
’, B – матрица перехода от  ’ к
’ к  .
.
Так как  ~
~  ’, то det A > 0. Так как det B = (det A)-1 (см. § 14), то det B > 0, то есть
’, то det A > 0. Так как det B = (det A)-1 (см. § 14), то det B > 0, то есть  ’ ~
’ ~  .
.
3) Транзитивность.
Пусть  ,
,  ’и
’и  ’’ – базисы пространства Vn такие, что
’’ – базисы пространства Vn такие, что  ~
~  ’ и
’ и  ’ ~
’ ~  ’’.
’’.
Пусть A – матрица перехода от  к
к  ’, B – матрица перехода от
’, B – матрица перехода от  ’ к
’ к  ’’.
’’.
Тогда AB – матрица перехода от базиса  к базису
к базису  ’’.
’’.
Так как det A > 0, det B > 0 и det AB = det A× det B (см. §14), то det AB > 0 и  ~
~  ’’.
’’.
Определение. Ориентацией пространства Vn будем называть класс эквивалентности одинаково ориентированных базисов пространства Vn.
Выбрать ориентацию – означает выбрать один из этих классов.
Определение. Ориентацией системы координат w в En будем называть, ориентацию пространства Vn, представителем которой является базис данной системы координат.
Определение. Ориентацией En, в котором введена аффинная система координат w, будем называть, ориентацию w.
То есть ориентацию в En задает фиксированная аффинная система координат.
Теорема. Ориентаций пространства Vn ровно две.
Доказательство.
1) Докажем, что ориентаций, по крайней мере, две (то есть две или больше).
Достаточно предъявить два базиса пространства Vn, которые ориентированы не одинаково.
Пусть  ,
,  ’ – базисы пространства Vn, такие, что e1’ = -e1, e2’ = e2, … en’ = en.
’ – базисы пространства Vn, такие, что e1’ = -e1, e2’ = e2, … en’ = en.
Тогда матрица перехода от  к
к  ’ – матрица A =
’ – матрица A =  , определитель этой матрицы det A = -1 < 0, то есть базисы
, определитель этой матрицы det A = -1 < 0, то есть базисы  и
и  ’ ориентированы не одинаково.
’ ориентированы не одинаково.
2) Докажем, что ориентаций не более двух (то есть две или меньше).
Достаточно показать, что не существует трех базисов пространства Vn, которые попарно ориентированы не одинаково.
Пусть  ,
,  ’и
’и  ’’ – базисы пространства Vn такие, что
’’ – базисы пространства Vn такие, что  и
и  ’,
’,  ’ и
’ и  ’’ ориентированы не одинаково. Докажем, что базисы
’’ ориентированы не одинаково. Докажем, что базисы  и
и  ’’ ориентированы одинаково.
’’ ориентированы одинаково.
Пусть A – матрица перехода от  к
к  ’, B – матрица перехода от
’, B – матрица перехода от  ’ к
’ к  ’’.
’’.
Тогда AB – матрица перехода от базиса  к базису
к базису  ’’.
’’.
Так как det A < 0, det B < 0 и det AB = det A× det B (см. §14), то det AB > 0 и  ~
~  ’’.
’’.
Замечания
1) О правых и левых тройках векторов.
Стандартный базис в декартовой системе координат в пространстве определяет класс эквивалентности одинаково ориентированных базисов, каждый из которых иногда называют правой тройкой. Геометрически это можно описать так: если три вектора этого базиса отложить от одной точки, то «поворот от первого вектора ко второму вдоль третьего вектора» подчиняется правилу правой руки. Есть и другие геометрические описания правила правой руки, которые можно найти в большинстве учебников по аналитической геометрии. Базис Vn , который не являе6тся правой тройкой, принято называть левой тройкой. Векторы левой тройки подчиняются правилу левой руки. Ясно, что ни одна из этих двух ориентаций (правые тройки, левые тройки) не является предпочтительной, они равноправны, но исторически сложилось так, что стандартной ориентацией считают ориентацию правой тройки.
2) Так как ориентаций пространства Vn ровно две, то можно говорить о двух базисах, которые ориентированы не одинаково, что они ориентированы противоположно.
Упражнение.
Меняется ли ориентация плоскости, на которой введена декартова система координат, при: (1) при параллельном переносе системы координат; (2) при повороте системы координат вокруг начала координат; (3) при симметрии системы координат относительно координатной оси; (4) при симметрии системы координат относительно биссектрис первой и третьей четвертей?
Скалярное произведение векторов
Vn
Пусть в En введена декартова система координат.
Определение. Скалярным произведением векторов  и
и  будем назвать число, которое равно сумме произведений соответствующих координат векторов
будем назвать число, которое равно сумме произведений соответствующих координат векторов  и
и  .
.
Обозначение:
| n = 1 |   = =
| xa xb |
| n = 2 | xa xb + ya yb | |
| n = 3 | xa xb + ya yb + za zb |
Замечания.
1) Ясно, что скалярное произведение – это отображение Vn ´ Vn ® R.
2) Пока не доказано, что скалярное произведение векторов не зависит от выбора декартовой системы координат. Возможно ли, что, вычислив скалярное произведение двух векторов в разных системах координат, мы получим различные результаты?
Теорема. (Свойства скалярного произведения)
1) Симметричность: 
 =
= 
 для любых векторов
для любых векторов  ,
,  Î Vn ;
Î Vn ;
2) Линейность по первому аргументу:
(  +
+  )
)  =
= 
 +
+ 
 для любых векторов
для любых векторов  ,
,  ,
,  Î Vn,
Î Vn,
(l  )
)  = l
= l 
 для любых векторов
для любых векторов  ,
,  Î Vn, для любого числа l Î R;
Î Vn, для любого числа l Î R;
3) Линейность по второму аргументу:
 (
(  +
+  ) =
) = 
 +
+ 
 для любых векторов
для любых векторов  ,
,  ,
,  Î Vn,
Î Vn,
 (l
(l  )= l
)= l 
 для любых векторов
для любых векторов  ,
,  Î Vn, для любого числа l Î R;
Î Vn, для любого числа l Î R;
4) 
 = |
= |  |2 для любого вектора
|2 для любого вектора  Î Vn;
Î Vn;
5) q  = 0 для любого
= 0 для любого  Î Vn.
Î Vn.
Доказательство.
Свойства (1) – (3) непосредственно следуют из свойств суммы и произведения действительных чисел.
(4) Пусть  = (
= (  ), тогда
), тогда 
 = |
= |  |2= |
|2= |  |2 (для n = 3:
|2 (для n = 3: 
 = x2 + y2 + z2 = |
= x2 + y2 + z2 = |  |2)
|2)
(5) Пусть  = (
= (  ), тогда q
), тогда q  = q
= q  = 0 (для n = 3: q
= 0 (для n = 3: q  = 0x + 0y + 0z = 0)
= 0x + 0y + 0z = 0)
Замечания.
1) Отображение Vn ´ Vn ® R, обладающее свойствами (1) – (3) называется симметричной билинейной формой. Непосредственно из свойства (4) следует, что скалярный квадрат любого вектора – неотрицательное число, и он равен нулю только для нулевого вектора. Последнее означает, что скалярное произведение – это симметричная невырожденная положительно определённая билинейная форма.
2) Свойство (4) показывает, что скалярный квадрат любого вектора не зависит от выбора декартовой системы координат в En, так как длина вектора не зависит от этого выбора.
Теорема. (Корректность определения скалярного произведения)
Скалярное произведение не зависит от выбора декартовой системы координат.
Доказательство.
Пусть  ,
,  Î Vn.
Î Vn.
Рассмотрим скалярное произведение (  +
+  )(
)(  +
+  ):
):
(  +
+  )(
)(  +
+  ) = |
) = |  +
+  |2 (по свойству (4))
|2 (по свойству (4))
(  +
+  )(
)(  +
+  ) =
) = 
 +
+ 
 +
+ 
 +
+ 
 = |
= |  |2 + 2
|2 + 2 
 + |
+ |  |2 (по свойствам (1) – (4))
|2 (по свойствам (1) – (4))
Так, что 
 = 1/2 (|
= 1/2 (|  +
+  |2 - |
|2 - |  |2 - |
|2 - |  |2)
|2)
Видно, что значение правой части равенства не зависит от выбора системы координат, так что значение и левой части равенства (то есть скалярное произведение векторов  и
и  ) не зависит от выбора системы координат.
) не зависит от выбора системы координат.
Определение. Углом между двумя ненулевыми векторами  ,
,  Î Vn будем называть угол AOB, где точки O,A,B Î En такие, что
Î Vn будем называть угол AOB, где точки O,A,B Î En такие, что  =
=  ,
,  =
=  .
.

РИС. 29
Замечание.
Угол между ненулевыми векторами не зависит от выбора точки O, от которой откладываются эти векторы.
Определение. Два вектора будем называть ортогональными, если хотя бы один из них нулевой или угол между ними прямой.
Обозначение:  ^
^ 
Теорема.(Геометрический смысл скалярного произведения).
Для любых двух ненулевых векторов  ,
,  Î Vn
Î Vn

 = |
= |  | |
| |  | cos j, где j – угол между векторами
| cos j, где j – угол между векторами  и
и  .
.
Доказательство.
Будем считать, что n = 3. Для остальных случаев доказательство аналогично.
Введем декартову систему координат такую, что  = (|
= (|  |, 0, 0),
|, 0, 0),  = (|
= (|  |cosj, |
|cosj, |  |sinj, 0).
|sinj, 0).
Тогда по определению скалярного произведения 
 = |
= |  | |
| |  | cosj.
| cosj.
Замечание.
При доказательстве данной теоремы существенно использовалось то, что значение скалярного произведения не зависит от выбора системы координат.
Следствие.  ^
^  Û
Û 
 = 0
= 0
Доказательство.
1) Пусть  ^
^  , тогда
, тогда  = q или
= q или  = q или j =
= q или j =  , где j – угол между векторами
, где j – угол между векторами  и
и  .
.
Тогда |  | = 0 или |
| = 0 или |  | = 0 или cosj = 0, то есть
| = 0 или cosj = 0, то есть 
 = 0
= 0
2) Пусть 
 = 0, то есть |
= 0, то есть |  | |
| |  | cos j = 0. Значит |
| cos j = 0. Значит |  | = 0 или |
| = 0 или |  | = 0 или cosj = 0 , то есть
| = 0 или cosj = 0 , то есть  = q или
= q или  = q или j =
= q или j =  , следовательно,
, следовательно,  ^
^  .
.
Следствие.(Неравенство Коши-Буняковского).
| 
 | £ |
| £ |  | |
| |  | для любых двух векторов
| для любых двух векторов  ,
,  Î Vn .
Î Vn .
Доказательство.
1) Для ненулевых векторов: | 
 | = |
| = |  | |
| |  | |cosj| £ |
| |cosj| £ |  | |
| |  |, так как |cosj| £ 1 .
|, так как |cosj| £ 1 .
2) Если  = q или
= q или  = q, то
= q, то 
 = 0 и |
= 0 и |  | |
| |  | = 0, так что неравенство справедливо и в этом случае.
| = 0, так что неравенство справедливо и в этом случае.
Замечание.
Итак, |  |2 |
|2 |  |2 - |
|2 - | 
 |2 ³ 0, более того, ясно, что |
|2 ³ 0, более того, ясно, что |  |2 |
|2 |  |2 - |
|2 - | 
 |2 = 0 Û
|2 = 0 Û  | |
| |  .
.
Определение. Базис пространства Vn называется ортонормированным, если векторы этого базиса имеют длину 1 и попарно ортогональны.
То есть базис  = (e1 e2 … en) ортонормированный тогда, и только тогда, когда
= (e1 e2 … en) ортонормированный тогда, и только тогда, когда  (где i,j Î {1,2,…,n})
(где i,j Î {1,2,…,n})
Замечание.
Ясно, что декартова система координат – это аффинная система координат с ортонормированным базисом. Поэтому матрица перехода от одной декартовой системы координат к другой декартовой системы координат – это матрица перехода от одного ортонормированного базиса к другому ортонормированному базису. Можно доказать, что:
(1) для таких базисов матрица обратного перехода получается из матрицы перехода операцией транспонирования (строки одной матрицы становятся столбцами другой матрицы);
(2) определитель такой матрицы перехода по модулю равен 1.
Условие (1) является необходимым и достаточным для того, чтобы матрица бала матрицей перехода между декартовыми системами координат.
Условие (2) является необходимым, но не достаточным для того, чтобы матрица бала матрицей перехода между декартовыми системами координат.
§ 19. Косое произведение векторов в V2
Из предыдущего параграфа обратим внимание на необходимое и достаточное условие коллинеарности векторов: |  |2 |
|2 |  |2 - |
|2 - | 
 |2 = 0 Û
|2 = 0 Û  | |
| |  .
.
Пусть на плоскости E2 зафиксирована декартова система координат.
Пусть  = (xa, ya),
= (xa, ya),  = (xb, yb). Рассмотрим выражение |
= (xb, yb). Рассмотрим выражение |  |2 |
|2 |  |2 - |
|2 - | 
 |2 в координатах:
|2 в координатах:
|  |2 |
|2 |  |2 - |
|2 - | 
 |2 = (xa2 + ya 2) (xb2 + yb2) – (xa xb + ya yb)2 = (xa yb - ya xb)2
|2 = (xa2 + ya 2) (xb2 + yb2) – (xa xb + ya yb)2 = (xa yb - ya xb)2
Итак, два вектора  ,
,  Î V2 коллинеарны, тогда и только тогда, когда xa yb - ya xb = 0.
Î V2 коллинеарны, тогда и только тогда, когда xa yb - ya xb = 0.
Определение. Косым произведением векторов  ,
,  Î V2 в данной системе координат w будем называть число, которое вычисляется по формуле xa yb - ya xb.
Î V2 в данной системе координат w будем называть число, которое вычисляется по формуле xa yb - ya xb.
Обозначение:  Ùw
Ùw 
Замечание. Естественно возникает вопрос, насколько косое произведение зависит от системы координат.
Определение. Будем говорить, что параллелограмм ABCD натянут на не коллинеарные векторы  и
и  , если
, если  =
=  и
и  =
= 

РИС. 30
Теорема.
(1)  Ùw
Ùw  = 0 Û
= 0 Û  | |
| |  для любых векторов
для любых векторов  ,
,  Î V2, в любой декартовой системе координат w;
Î V2, в любой декартовой системе координат w;
(2) Если векторы  и
и  не коллинеарны, то |
не коллинеарны, то |  Ùw
Ùw  | = S, где S – площадь параллелограмма, натянутого на векторы
| = S, где S – площадь параллелограмма, натянутого на векторы  и
и  , в любой системе декартовой координат w;
, в любой системе декартовой координат w;
(3)  Ù
Ù  =
=  , где
, где  = (xa, ya),
= (xa, ya),  = (xb, yb), для любых векторов
= (xb, yb), для любых векторов  ,
,  Î V2;
Î V2;
(4)  Ùw
Ùw  =
=  Ùw’
Ùw’  , если декартовы системы координат w и w’ориентированы одинаково;
, если декартовы системы координат w и w’ориентированы одинаково;
 Ùw
Ùw  = -
= -  Ùw’
Ùw’  , если декартовы системы координат w и w’имеют противоположные ориентации.
, если декартовы системы координат w и w’имеют противоположные ориентации.
Доказательство.
Пункт (1) является прямым следствием определения;
(2) По определению косого произведения
|  Ùw
Ùw  |2 = |
|2 = |  |2 |
|2 |  |2- |
|2- | 
 |2 = |
|2 = |  |2 |
|2 |  |2 - |
|2 - |  |2|
|2|  |2cos2j = |
|2cos2j = |  |2 |
|2 |  |2(1 – cos2j) = |
|2(1 – cos2j) = |  |2 |
|2 |  |2sin2j = S2 (где j - угол между векторами
|2sin2j = S2 (где j - угол между векторами  и
и  );
);
(3) По определению определителя  = xa yb - ya xb;
= xa yb - ya xb;
(4) Пусть A – матрица перехода от системы координат w’ к системе координат w.
Тогда для любого вектора  = A
= A  , где
, где  - координаты вектора в системе w,
- координаты вектора в системе w,  - координаты вектора в системе координат w’.
- координаты вектора в системе координат w’.
 Ùw’
Ùw’  =
= 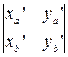 =
=  = det A (xa yb - ya xb) = det A
= det A (xa yb - ya xb) = det A  Ùw
Ùw 
Если w ~ w’, то det A = 1 и  Ùw
Ùw  =
=  Ùw’
Ùw’  , иначе det A = -1 и
, иначе det A = -1 и  Ùw
Ùw  = -
= -  Ùw’
Ùw’  .
.
Замечание.
Свойства (1), (2), (4) из вышеуказанной теоремы показывают, что модуль косого произведения векторов не зависит от выбора декартовой системы координат, а при смене системы координат у косого произведения векторов измениться знак, если новая и старая системы координат ориентированы противоположно.
Следствие.
Для неколлинеарных векторов  ,
,  Î V2 косое произведение положительно в системе координат w тогда, и только тогда, когда базиса системы координат w и пара векторов {
Î V2 косое произведение положительно в системе координат w тогда, и только тогда, когда базиса системы координат w и пара векторов {  ,
,  } ориентированы одинаково. (То есть,
} ориентированы одинаково. (То есть,  Ùw
Ùw  > 0 Û w ~ {
> 0 Û w ~ {  ,
,  })
})
Доказательство.
Если векторы  и
и  не коллинеарны, то пара {
не коллинеарны, то пара {  ,
,  } образует базис пространства .
} образует базис пространства .
Определитель матрицы перехода от фиксированного в декартовой системе координат базиса к базису {  ,
,  }будет следующим:
}будет следующим:  =
=  =
=  Ùw
Ùw  .
.
Так, что по определению одинаковой ориентированности базисов  Ùw
Ùw  > 0 тогда, и только тогда, когда w ~ {
> 0 тогда, и только тогда, когда w ~ {  ,
,  }.
}.
Замечание. В дальнейшем будем опускать знак системы координат в обозначении косого произведения, и считать, что на плоскости зафиксирована декартова система координат.
Теорема. (Алгебраические свойства косого произведения).
(1) Антисимметричность:  Ù
Ù  = -
= -  Ù
Ù  для любых двух векторов
для любых двух векторов  ,
,  Î V2;
Î V2;
(2) Линейность по первому аргументу:
(  +
+  ) Ù
) Ù  =
=  Ù
Ù  +
+  Ù
Ù  для любых векторов
для любых векторов  ,
,  ,
,  Î V2,
Î V2,
(l  ) Ù
) Ù  = l
= l  Ù
Ù  для любых векторов
для любых векторов  ,
,  Î V2, для любого числа l Î R;
Î V2, для любого числа l Î R;
(3) Линейность по второму аргументу:
 Ù(
Ù(  +
+  ) =
) =  Ù
Ù  +
+  Ù
Ù  для любых векторов
для любых векторов  ,
,  ,
,  Î V2,
Î V2,
 Ù (l
Ù (l  ) = l
) = l  Ù
Ù  для любых векторов
для любых векторов  ,
,  Î V2, для любого числа l Î R.
Î V2, для любого числа l Î R.
Доказательство.
Свойства (1) – (2) являются прямым следствием определения.
Пусть векторы  ,
,  и
и  имеют следующие координаты:
имеют следующие координаты:
 = (xa, ya),
= (xa, ya),  = (xb, yb),
= (xb, yb),  = (xc, yc).
= (xc, yc).
(1)  Ù
Ù  = xa yb - ya xb = - (ya xb - xa yb) = -
= xa yb - ya xb = - (ya xb - xa yb) = -  Ù
Ù  ;
;
(2) (  +
+  ) Ù
) Ù  = (xa + xb)yc – (ya + yb)xc = (xa yc - ya xc) + (xb yc - yb xc) =
= (xa + xb)yc – (ya + yb)xc = (xa yc - ya xc) + (xb yc - yb xc) =  Ù
Ù  +
+


