 |
Главная |
Однородные уравнения второго порядка с постоянными коэффициентами
|
из
5.00
|
Линейным однородным дифференциальным уравнением 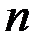 -го порядка с постоянными коэффициентами называется уравнение вида:
-го порядка с постоянными коэффициентами называется уравнение вида:
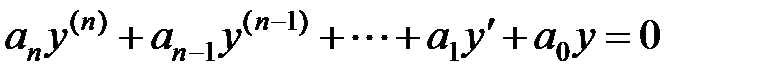 ,
,
где  – действительные числа.
– действительные числа.
Частным случаем однородного уравнения второго порядка является:  , где
, где  и
и  – постоянные коэффициенты.
– постоянные коэффициенты.
Теорема 1.Если  – решение уравнения
– решение уравнения  , то и
, то и  , где
, где  – произвольная постоянная, тоже будет решением этого уравнения.
– произвольная постоянная, тоже будет решением этого уравнения.
Теорема 2. Если  – решения уравнения
– решения уравнения  , то их сумма тоже является решением этого уравнения.
, то их сумма тоже является решением этого уравнения.
Два решения  называются линейно независимыми на множестве
называются линейно независимыми на множестве  , если их отношение не равно постоянному числу. В противоположном случае решения
, если их отношение не равно постоянному числу. В противоположном случае решения  называются линейно зависимыми.
называются линейно зависимыми.
Теорема 3. Если  – независимые решения уравнения
– независимые решения уравнения  , то
, то  есть общее решение уравнения.
есть общее решение уравнения.
Теорема 4. Если решения уравнения  линейно зависимые, то решение
линейно зависимые, то решение  не будет общим решением уравнения.
не будет общим решением уравнения.
Решение  является частным решением уравнения, потому что оно зависит от одной произвольной постоянной
является частным решением уравнения, потому что оно зависит от одной произвольной постоянной  . Таким образом, из теоремы 3можно сделать вывод: чтобы найти общее решение уравнения, нужно найти два его линейно независимых решения
. Таким образом, из теоремы 3можно сделать вывод: чтобы найти общее решение уравнения, нужно найти два его линейно независимых решения  и тогда
и тогда 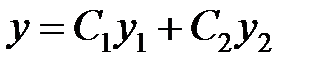 будет общим решением этого уравнения.
будет общим решением этого уравнения.
Будем искать частное решение уравнения  в виде показательной функции
в виде показательной функции  . Подставив в уравнение первую и вторую производные частного решения и учитывая, что
. Подставив в уравнение первую и вторую производные частного решения и учитывая, что  , после упрощения получим уравнение:
, после упрощения получим уравнение:  .
.
Это уравнение относительно  называется характеристическим уравнением данного однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
называется характеристическим уравнением данного однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
Чтобы получить характеристическое уравнение, достаточно производные  ,
,  и функцию
и функцию  заменить на соответствующие степени величины
заменить на соответствующие степени величины 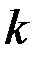 , рассматривая при этом функцию
, рассматривая при этом функцию  как производную нулевого порядка.
как производную нулевого порядка.
Решив характеристическое уравнение, найдем значения 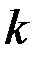 :
:
 .
.
Рассмотрим разные случаи решений характеристического уравнения, от которых зависит вид частного решения:
1. Если  , корни уравнения действительные и разные:
, корни уравнения действительные и разные:  .
.
В этом случае  ;
;  – линейно независимые решения уравнения. Частные решения уравнения
– линейно независимые решения уравнения. Частные решения уравнения  и
и  линейно независимы, потому что их соотношение не является постоянной величиной.
линейно независимы, потому что их соотношение не является постоянной величиной.
Тогда в соответствии с теоремой 3 общее решение уравнения будет:
 . (*)
. (*)
Пример 1. Найти общее решение дифференциального уравнения: 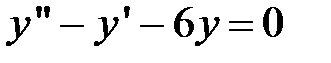 .
.
Решение.
Составим характеристическое уравнение:  . Это уравнение имеет разные действительные корни:
. Это уравнение имеет разные действительные корни:  . Им соответствуют два частных решения:
. Им соответствуют два частных решения:  ,
,  .
.
Следовательно, общее решение имеет вид:  .
.
2. Если  , то корни характеристического уравнения действительны и равны:
, то корни характеристического уравнения действительны и равны:  .
.
В этом случае  – частное решение уравнения. Второе частное решение найдем в виде
– частное решение уравнения. Второе частное решение найдем в виде 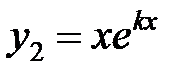 . Тогда в соответствии с теоремой 3 общее решение уравнения будет:
. Тогда в соответствии с теоремой 3 общее решение уравнения будет:
 . (**)
. (**)
Пример 2. Найти общее решение уравнения: 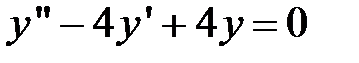 .
.
Решение.
Запишем характеристическое уравнение этого дифференциального уравнения:  . Его корни:
. Его корни: 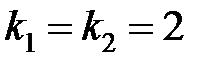 . То есть уравнение имеет один двукратный действительный корень.
. То есть уравнение имеет один двукратный действительный корень.
Ему соответствуют два частных решения уравнения: 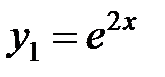 ,
,  . Общее решение уравнения имеет вид:
. Общее решение уравнения имеет вид:  .
.
3. Если  , то уравнение имеет комплексно-сопряженные корни:
, то уравнение имеет комплексно-сопряженные корни:  , где
, где  ;
;  .
.
В этом случае частные решения уравнения имеют вид:
 ;
;  .
.
Тогда в соответствии с теоремой 3 общее решение уравнение будет:
 . (***)
. (***)
Пример 3. Найти общее решение уравнения:  .
.
Решение.
Запишем характеристическое уравнение:  . Оно имеет комплексные корни:
. Оно имеет комплексные корни:  . То есть
. То есть  ;
;  . Этим корням соответствуют два частных решения:
. Этим корням соответствуют два частных решения:
 и
и  .
.
Общее решение уравнения имеет вид:
 .
.
|
из
5.00
|
Обсуждение в статье: Однородные уравнения второго порядка с постоянными коэффициентами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

