 |
Главная |
Лекция 12. Системы дифференциальных уравнений
|
из
5.00
|
Достаточно часто для описания исследуемых процессов не достаточно одного дифференциального уравнения, поэтому используется их совокупность.
Совокупность  линейных дифференциальных уравнений первого порядка с
линейных дифференциальных уравнений первого порядка с  неизвестными функциями
неизвестными функциями  от одной независимой переменной
от одной независимой переменной  :
:

где коэффициенты  и свободные члены
и свободные члены 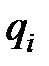 (
(  ) являются функциями от
) являются функциями от  , называется системой линейных дифференциальных уравнений. Если уравнения системы решены относительно производных, то система линейных дифференциальных уравнений называется нормальной.
, называется системой линейных дифференциальных уравнений. Если уравнения системы решены относительно производных, то система линейных дифференциальных уравнений называется нормальной.
Если коэффициенты системы являются постоянными величинами, то такая система называется системой дифференциальных уравнений с постоянными коэффициентами. При  система называется однородной, в противном случае
система называется однородной, в противном случае  неоднородной.
неоднородной.
Общим решением системы дифференциальных уравненийназывается совокупность  функций, которые зависят от независимой переменной
функций, которые зависят от независимой переменной 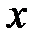 и
и  произвольных постоянных
произвольных постоянных  :
:
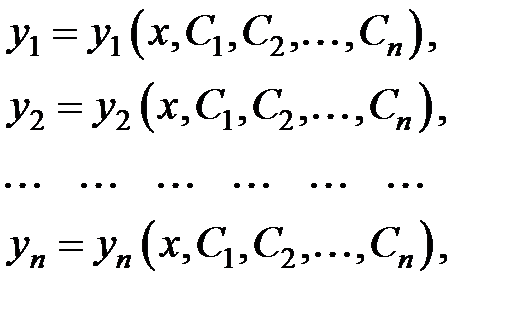
которые удовлетворяют все уравнения системы.
Если независимую переменную обозначить через  , то система принимает вид
, то система принимает вид 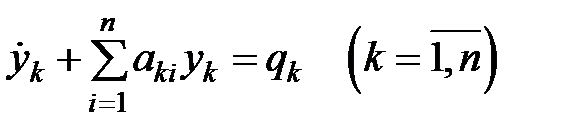 , где
, где  – производная первого порядка по аргументу
– производная первого порядка по аргументу  .
.
Задача Коши для системы дифференциальных уравненийзаключается в определении такого решения системы, которое удовлетворяет начальные условия:  ,
,  , ... ,
, ... , 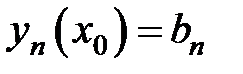 .
.
Методы решения системы дифференциальных уравнений
Одним из способов решения системы есть метод исключения, который предусматривает исключение  неизвестных функций, в результате чего система сводится к дифференциальному уравнению
неизвестных функций, в результате чего система сводится к дифференциальному уравнению  -го порядка относительно одной из неизвестных функций.
-го порядка относительно одной из неизвестных функций.
Пример 1.
Найдем решение системы дифференциальных уравнений:

Это нормальная система линейных дифференциальных уравнений. Применим для ее решения метод исключения. Продифференцируем первое уравнение системы:  .
.
Учитывая второе уравнение, имеем:
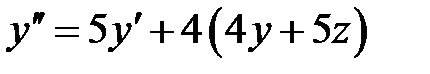

 .
.
По первому уравнению системы определяем, что  ,
,
тогда: 

 .
.
Следовательно, для определения функции  мы получили однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Характеристическое уравнение соответствующего однородного уравнения имеет вид:
мы получили однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Характеристическое уравнение соответствующего однородного уравнения имеет вид:  . Отсюда определяем корни:
. Отсюда определяем корни:  ,
,  .
.
Теперь записываем общее решение для функції  :
:
 .
.
Теперь находим функцию  , подставив в первое уравнение системы
, подставив в первое уравнение системы  и
и  , но сначала найдем
, но сначала найдем  :
:  .
.
 , или
, или 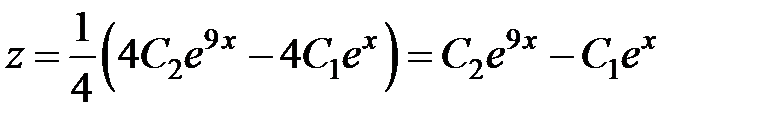 .
.
Следовательно, общее решение системы дифференциальных уравнений:  ,
,  .
.
Рассмотрим еще один метод решения системы дифференциальных уравнений, который называется алгебраическим.
Пусть задана нормальная система дифференциальных уравнений первого порядка

где  – постоянные величины,
– постоянные величины,  – неизвестны функции
– неизвестны функции  .
.
Систему можно записать как матричное уравнение:
 ,
,
где
 ,
,  ,
,  .
.
Частные решения системы будем искать в виде совокупности показательных функций:  ,
,  , ...,
, ...,  , где
, где  неопределенные постоянные, которые нужно найти.
неопределенные постоянные, которые нужно найти.
Подставляя эти функции в систему и сокращая на множитель  , получим систему линейных уравнений относительно
, получим систему линейных уравнений относительно 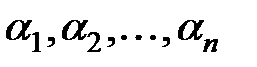 :
:

Найдем определитель этой системы:
 .
.
Если 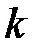 такое, что определитель
такое, что определитель  , то система уравнений имеет только тривиальное решение:
, то система уравнений имеет только тривиальное решение:  .
.
Нетривиальное решение система будет иметь лишь при таких 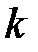 , при которых определитель этой системы будет равен нулю.
, при которых определитель этой системы будет равен нулю.
Следовательно, для определения 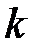 мы приходим к уравнению
мы приходим к уравнению  -го порядка:
-го порядка:
 .
.
Это уравнение называется характеристическим уравнением системы дифференциальных уравнений, его корни – корнями характеристического уравнения.
Рассмотрим только случай, когда корни характеристического уравнения действительные и разные.
Для каждого корня 
 записывают систему и определяют коэффициенты
записывают систему и определяют коэффициенты 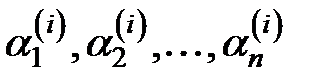 . Поскольку ранг матрицы системы равен
. Поскольку ранг матрицы системы равен  , то один из коэффициентов можно выбрать произвольно. Будем считать его равным единице.
, то один из коэффициентов можно выбрать произвольно. Будем считать его равным единице.
Тогда получаем частные решения системы:
для  :
:  ,
,  , ...,
, ...,  ;
;
для  :
: 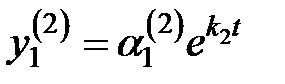 ,
,  , ...,
, ...,  ;
;
…………………………………………………………….
для  :
:  ,
,  , ...,
, ...,  .
.
Систему  частных решений
частных решений

называют фундаментальной системой решений на интервале  , если определитель
, если определитель

не равен нулю.
Соответственно, общее решение системы имеет вид:
 ,
,
 ,
,
……………………………………..
 ,
,
где 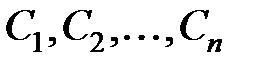 – произвольные постоянные.
– произвольные постоянные.
Пример 2.
Найдем общее решение системы дифференциальных уравнений:

Будем искать частые решения этой системы в виде  и
и 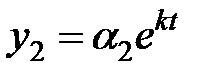 . Для определения неизвестных коэффициентов
. Для определения неизвестных коэффициентов  этих функций составляем характеристическое уравнение:
этих функций составляем характеристическое уравнение:
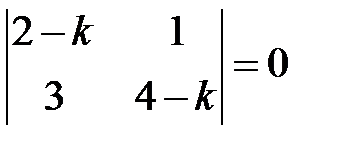 ,
,
откуда


 .
.
Корни уравнения  ,
,  .
.
При  система принимает вид:
система принимает вид: 
Отсюда  .
.
Пусть 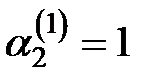 , тогда
, тогда  .
.
Следовательно, имеем решения:  ,
,  .
.
При  система имеет вид:
система имеет вид:

Отсюда  . Считая
. Считая  , получим
, получим  . Тогда:
. Тогда:
 ,
,  .
.
Таким образом, мы получили фундаментальную систему решений:
 ,
,  ,
,
 ,
,  .
.
Следовательно, общее решение системы имеет вид:
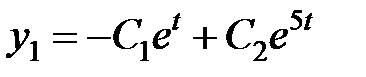 ,
,
 .
.
|
из
5.00
|
Обсуждение в статье: Лекция 12. Системы дифференциальных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

